Python堆与优先队列：数据结构中的隐形冠军

# 1. Python堆与优先队列基础

## 1.1 Python堆与优先队列概述
Python堆是一种特殊的数据结构，广泛应用于优先队列的设计中。优先队列允许元素按特定的优先级顺序进行处理。通过Python中的堆结构，我们可以高效地处理具有优先级的元素集合，这些元素可以是数据点、任务或其他任何需要排序的实体。

## 1.2 堆的必要性与应用领域
为什么需要使用堆结构？因为在很多场景下，我们需要快速获取并处理优先级最高的元素。例如，在操作系统中管理进程、在银行系统中处理交易请求、或者在数据挖掘中筛选出最大或最小的k个元素等。通过堆结构，我们可以实现对这些需求的高效处理。

## 1.3 Python中堆的实现与优势
在Python中，堆通常通过堆队列算法模块（heapq）来实现。Python的heapq模块提供了一套简洁的API来创建和管理堆。利用堆实现的优先队列相比于数组或链表等其他数据结构，在进行插入和删除操作时可以达到对数级别的时间复杂度，这在大规模数据处理中优势显著。

代码块示例：

import heapq

# 创建一个最小堆
min_heap = []
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 5)
heapq.heappush(min_heap, 2)

# 弹出最小元素
print(heapq.heappop(min_heap))  # 输出: 1

上述代码展示了如何使用Python heapq模块创建一个最小堆，并弹出最小元素。这个基础操作是优先队列实现的核心部分，为更复杂的应用打下了基础。

# 2. 堆的理论基础及其在优先队列中的应用

在探索数据结构的世界中，堆（Heap）是一种特殊的完全二叉树，其特性保证了堆顶元素的特定性质——在最大堆中，堆顶元素是所有节点中的最大值；在最小堆中，堆顶元素则是最小值。这种特性使堆成为实现优先队列的完美结构。优先队列是一种抽象数据类型，支持在任何时刻都能快速获取到当前“优先级最高”的元素。本章将深入探讨堆的理论基础，以及它在优先队列中的应用。

## 2.1 堆的概念和分类

堆作为一种数据结构，不仅可以用来实现优先队列，还可以用于诸如堆排序等其他算法中。堆的分类主要基于它的性质，下面将讨论最大堆和最小堆的差异以及它们的数学模型和性质。

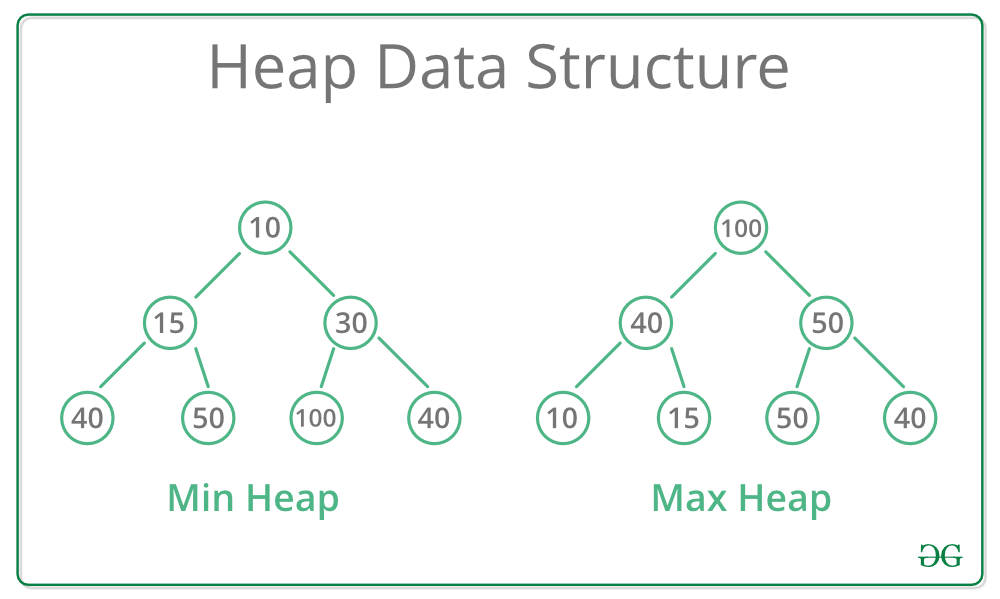
### 2.1.1 最大堆和最小堆的区别

最大堆是一种特殊的二叉树，满足以下性质：
- 完全二叉树结构：除了最后一层外，每一层都被完全填满，且最后一层的节点都靠左排列。
- 最大堆性质：任何一个父节点的值都大于或等于其子节点的值。

最小堆则相反：
- 同样是完全二叉树结构。
- 最小堆性质：任何一个父节点的值都小于或等于其子节点的值。

这两个性质导致最大堆经常被用于需要找到最大元素的场景，而最小堆则适用于需要找到最小元素的场景。

### 2.1.2 堆的数学模型和性质

堆的数学模型可以抽象为树状结构，但以数组形式存储。在数组表示中，对于任意位于数组索引 i 的元素，其子节点可以表示为 2i+1 和 2i+2（如果存在），而其父节点则为 (i-1)/2（向下取整）。

堆的性质不仅限于上述的树结构性质，还包括以下数学性质：
- 堆的高度 h = ⌊log₂n⌋，其中 n 是堆中元素的数量。
- 在堆中，所有层级除最后一层外都是满的，最后一层从左至右填满。
- 堆是近似平衡的，因为完全二叉树的性质，堆操作的时间复杂度可以保持在对数级别。

## 2.2 堆的实现机制

实现堆的关键在于理解它的数组表示以及如何维护堆的性质。本小节将介绍堆的数组表示、构造过程和调整方法。

### 2.2.1 堆的数组表示

堆通过数组表示时，数组中的第 i 个元素与完全二叉树中节点的对应关系为：
- 节点值存储在数组的第 i 个位置。
- 节点的左子节点值存储在 2i+1 的位置。
- 节点的右子节点值存储在 2i+2 的位置。
- 节点的父节点值存储在 (i-1)/2 的位置。

### 2.2.2 堆的构造过程和调整方法

堆的构造过程是一个将无序的元素调整为堆的过程。它通常包括两个步骤：首先将元素按照完全二叉树的顺序放入数组中，然后从最后一个非叶子节点开始向上进行下沉调整（sift down）操作，确保所有节点都符合堆的性质。

下沉调整的过程是这样的：
- 比较当前节点与其子节点的值。
- 如果子节点中的较小者（或较大者，取决于是最大堆还是最小堆）的值大于（或小于）当前节点的值，则交换它们的位置。
- 重复上述步骤，直到当前节点成为合法的堆节点。

下面是一个下沉调整的 Python 代码示例：

def sift_down(heap, i, end):
    parent = i
    child = 2 * i + 1
    while child <= end:
        # 如果存在右子节点且大于左子节点，则考虑右子节点
        if child + 1 <= end and heap[child] < heap[child + 1]:
            child += 1
        # 如果父节点已经大于其最大（或最小）子节点，则已满足堆性质
        if heap[parent] >= heap[child]:
            return
        # 否则，交换它们并继续调整
        heap[parent], heap[child] = heap[child], heap[parent]
        parent = child
        child = 2 * child + 1

def build_max_heap(heap):
    for i in range((len(heap)-2)//2, -1, -1):
        sift_down(heap, i, len(heap)-1)
    return heap

该示例中，`sift_down` 函数负责执行下沉操作，`build_max_heap` 函数用于从任意顺序的数组构建最大堆。

## 2.3 优先队列的工作原理

优先队列是一种抽象数据类型，它管理了一组元素并支持两个基本操作：`insert`（插入）和 `extract_max` 或 `extract_min`（提取最大或最小元素）。在本小节中，我们将详细解析优先队列的定义、操作，以及堆与优先队列之间的紧密联系。

### 2.3.1 优先队列的定义和操作

在优先队列中，每个元素都有一个与之相关联的优先级。优先级最高的元素会被首先删除。优先队列的操作通常包括：
- `insert`: 将一个新元素添加到队列中，保证队列的优先级顺序。
- `extract_max`/`extract_min`: 移除并返回队列中优先级最高（或最低）的元素。

### 2.3.2 堆与优先队列的关系

堆是实现优先队列的有效数据结构，原因如下：
- 快速访问：堆顶元素总是具有最高或最低优先级，这使得`extract_max`/`extract_min`操作可以快速完成。
- 效率保证：插入操作可以通过下沉调整快速完成，通常在 O(log n) 时间复杂度内。
- 结构紧凑：使用数组表示的堆可以避免动态调整大小的开销，并且可以高效地利用内存。

综上所述，堆为优先队列提供了一个高效实现框架，使其在许多需要优先级处理的场景中成为不二选择，例如操作系统中的任务调度、数据压缩算法中的哈夫曼编码等。接下来的章节，我们将深入了解 Python 中如何操作堆，以及优先队列的实际应用案例。

# 3. Python中堆的实践操作

## 3.1 Python内置堆操作
### 3.1.1 使用heapq模块
在Python中，`heapq`模块提供了一种堆队列算法的实现，这种算法常用作优先队列。使用`heapq`模块可以轻松创建最小堆，而最大堆可以通过对元素取负值来实现。堆的基本操作包括添加元素到堆中、从堆中弹出最小元素以及堆的构建等。

下面是一个简单的例子，展示了如何使用`heapq`模块来创建一个最小堆，并添加和删除元素：

import heapq

# 创建一个空堆
min_heap = []

# 向堆中添加元素
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 2)

print("堆中的元素：", min_heap)

# 弹出最小元素
print("弹出最小元素：", heapq.heappop(min_heap))

print("更新后的堆：", min_heap)

在上述代码中，我们首先导入了`heapq`模块，然后创建了一个空堆`min_heap`。接着使用`heappush`函数向堆中添加了三个元素。`heappop`函数用于从堆中弹出最小元素。

### 3.1.2 堆的创建和管理
创建堆是优先队列应用中的一个重要步骤。Python的`heapq`模块提供了`heapify`函数，可以将一个列表转换成一个有效的堆，这对于已存在的数据集合进行堆操作非常有效。

下面的代码展示了如何使用`heapify`函数：

import heapq

# 创建一个普通列表
data = [2, 1, 5, 3, 4]

# 将列表转换为最小堆
heapq.heapify(data)

print("堆化后的数据：", data)

# 堆中添加新元素
heapq.heappush(data, 0)

print("添加元素后的堆：", data)

# 弹出最小元素
print("弹出最小元素：", heapq.heappop(data))

print("再次堆化后的数据：", data)

在这个例子中，我们首先创建了一个普通列表`data`，然后使用`heapq.heapify`将其转换为最小堆。之后，我们向这个堆中添加了一个新元素并弹出了最小元素。注意每次弹出操作后，堆的性质仍然保持不变。

堆的管理不仅包括创建堆，还需要定期维护堆的结构。例如，当堆的某一部分被修改后，可以通过调用`heappop`和`heappush`来确保堆结构的正确性。

## 3.2 堆在算法问题中的应用实