【图论与Python】：构建复杂网络模型的算法基础

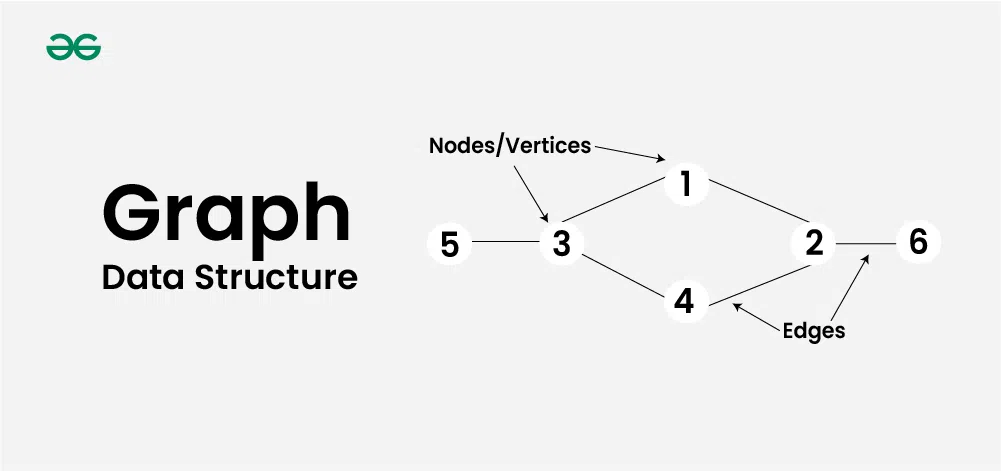
# 1. 图论与复杂网络基础

图论是数学的一个分支，它研究由一系列顶点（或节点）和连接这些顶点的边组成的图形。在现实世界中，图论被广泛应用于计算机科学、网络理论、运筹学等多个领域。复杂网络则是图论的一个现代应用，它专注于图的拓扑属性、演进过程以及复杂性分析。随着计算机和网络技术的发展，对图论及其在复杂网络中应用的理解变得尤为重要。

## 1.1 图的基本概念与分类

### 1.1.1 图的定义和表示方法
图由一组顶点（nodes）和连接顶点对的边（edges）组成。一个简单的图表示可以是`G = (V, E)`，其中`V`是顶点集，`E`是边集。图的表示方法有邻接矩阵和邻接列表两种方式。邻接矩阵适合表示稠密图，邻接列表则在稀疏图中更为高效。

# 示例：使用Python实现邻接矩阵表示图
V = ['A', 'B', 'C', 'D']
E = [('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'A')]
adj_matrix = {v: [0]*len(V) for v in V}

for edge in E:
    adj_matrix[edge[0]][V.index(edge[1])] = 1
    adj_matrix[edge[1]][V.index(edge[0])] = 1

### 1.1.2 图的分类及其特征
图可以分为无向图、有向图、加权图和非加权图等。无向图中的边没有方向，而有向图的边有方向。加权图的边被赋予一定的权重，而非加权图则没有。根据顶点的连接方式，图还可以分为完全图、二分图和循环图等。这些不同的分类方式对图的属性和相关算法有着重要影响。

# 2. 图论中的核心算法与理论

## 2.1 图的基本概念与分类
图是图论研究中最基本的结构，用于描述实体间的关系。本小节将详细介绍图的定义、表示方法以及如何对图进行分类。

### 2.1.1 图的定义和表示方法

图由顶点集合和边集合构成。在数学上，图G可以表示为G=(V,E)，其中V是顶点集，E是边集。边可以是有向的或无向的，可以有权重或无权重。图的表示方法主要有邻接矩阵和邻接表。

#### 邻接矩阵
邻接矩阵是一个二维数组，用于表示图中顶点之间的连接关系。如果顶点i和顶点j之间有边，则矩阵中的元素a[i][j]为1（或边的权重），否则为0。

# 邻接矩阵表示图的Python代码示例
import numpy as np

def create_adjacency_matrix(edges, vertices):
    matrix = np.zeros((vertices, vertices))
    for i, j in edges:
        matrix[i][j] = 1  # 或边的权重
    return matrix

# 例如，对于无向图：
edges = [(0, 1), (0, 2), (1, 2), (2, 3)]
vertices = 4  # 顶点数量从0开始计数
adj_matrix = create_adjacency_matrix(edges, vertices)
print(adj_matrix)

#### 邻接表
邻接表使用列表存储每个顶点的邻居信息。每个顶点对应一个列表，列表中包含所有与该顶点相邻的顶点。

# 邻接表表示图的Python代码示例
def create_adjacency_list(edges, vertices):
    adj_list = [[] for _ in range(vertices)]
    for i, j in edges:
        adj_list[i].append(j)
        adj_list[j].append(i)  # 无向图
    return adj_list

# 对于相同无向图的例子：
adj_list = create_adjacency_list(edges, vertices)
print(adj_list)

### 2.1.2 图的分类及其特征

根据顶点的连接情况，图可以分为无向图和有向图。边也可以是有权的或无权的，从而形成无权无向图、无权有向图、有权无向图和有权有向图。特殊类型的图还包括完全图、循环图、二部图等。

- 完全图：图中任意两个不同顶点之间都存在边。
- 循环图：有向图中，每个顶点都有一条边指向自己。
- 二部图：图的顶点集可分割为两个互不相交的子集，图中每条边连接的两个顶点分别属于这两个不同的顶点集。

每种图的特征决定了适合它的算法和应用场景。例如，有向图多用于表示网络流量，而无向图则多用于表示社交网络等。

## 2.2 图的遍历算法

图遍历算法是图论中的基础算法之一，用于访问图中的所有顶点。本小节将介绍两种常见的图遍历算法：深度优先搜索（DFS）和广度优先搜索（BFS）。

### 2.2.1 深度优先搜索（DFS）

深度优先搜索是一种用于遍历或搜索树或图的算法。该算法沿着图的边进行，并在可能时深入到每个分支，直到达到一个节点没有未访问的邻居节点为止。

# DFS算法实现的Python代码示例
def dfs(graph, start):
    visited, stack = set(), [start]
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            visited.add(vertex)
            stack.extend(graph[vertex] - visited)
    return visited

# 对于无向图：
graph = {
    0: {1, 2},
    1: {0, 3},
    2: {0},
    3: {1}
}
print(dfs(graph, 0))

DFS的时间复杂度为O(V+E)，其中V是顶点数，E是边数。DFS适用于求解路径问题，例如回路、环等。

### 2.2.2 广度优先搜索（BFS）

广度优先搜索算法从一个顶点开始，首先访问所有邻近的顶点，然后再对每个邻近顶点做同样的操作。与DFS不同，BFS会优先访问距离根节点近的顶点。

# BFS算法实现的Python代码示例
from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            visited.add(vertex)
            queue.extend(graph[vertex] - visited)
    return visited

# 对于相同无向图的例子：
print(bfs(graph, 0))

BFS的时间复杂度也是O(V+E)。BFS可以用来求解最短路径，比如在无权图中从一个顶点到其他顶点的最短路径。

## 2.3 最短路径算法

在图中找到两个顶点之间的最短路径是一个经典的问题。常见的算法包括Dijkstra算法、Bellman-Ford算法和Floyd-Warshall算法。

### 2.3.1 Dijkstra算法

Dijkstra算法用于在加权图中找到一个顶点到其他所有顶点的最短路径，假设所有边的权重都是正数。

# Dijkstra算法实现的Python代码示例
import heapq

def dijkstra(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        if current_distance > distances[current_vertex]:
            continue

        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

# 对于有权无向图的例子：
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}
print(dijkstra(graph, 'A'))

Dijkstra算法的时间复杂度为O((V+E)logV)，其中V是顶点数，E是边数。

### 2.3.2 Bellman-Ford算法

Bellman-Ford算法同样用于求解单源最短路径问题，适用于带有负权边的图，但不能有负权回路。

# Bellman-Ford算法实现的Python代码示例
def bellman_ford(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0

    for _ in range(len(graph) - 1):
        for vertex in graph:
            for neighbor, weight in graph[vertex].items():
                if distances[vertex] + weight < distances[neighbor]:
                    distances[neighbor] = distances[vertex] + weight

    return distances

# 示例图同上
print(bellman_ford(graph, 'A'))

Bellman-Ford算法的时间复杂度为O(VE)。

### 2.3.3 Floyd-Warshall算法

Floyd-Warshall算法用于寻找所有顶点对之间的最短路径。这是一个动态规划算法，计算图中所有顶点的最短路径。

# Floyd-Warshall算法实现的Python代码示例
def floyd_warshall(graph):
    distance = {vertex: {vertex: 0 for vertex in graph} for vertex in graph}
    for vertex in graph:
        for vertex_1 in graph:
            if vertex == vertex_1:
                distance[vertex][vertex_1] = 0
            else:
                distance[vertex][vertex_1] = float('infinity')

    for k in graph:
        for i in graph:
            for j in graph:
                if distance[i][k] + distance[k][j] < distance[i][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]

    return distance

# 示例图同上
print(floyd_warshall(graph))

Floyd-Warshall算法的时间复杂度为O(V^3)。

## 2.4 连通性问题与算法

连通性问题探讨图是否是连通的，即图中任意两个顶点是否相互可达。本小节将介绍最小生成树算法和强连通分量与弱连通分量。

### 2.4.1 最小生成树算法（如Kruskal和Prim算法）

最小生成树是一幅加权图的树形子图，包含所有顶点，并且具有最小的边的权重和。Kruskal算法和Prim算法是求解最小生成树的两种著名算法。

#### Kruskal算法
Kruskal算法按照边的权重顺序，从最小权重的边开始，添加边到最小生成树中，但不形成环。

# Kruskal算法实现的Python代码示例
class DisjointSet:
    def __init__(self, vertices):
        self.parent = {vertex: vertex for vertex in vertices}
        self.rank = {vertex: 0 for vertex in vertices}

    def find(self, node):
        if self.parent[node] != node:
            self.parent[node]