【动态规划与Python实战】：分治策略解决复杂问题的技巧

# 1. 动态规划与分治策略概述

在解决复杂计算问题时，动态规划（Dynamic Programming，DP）和分治策略（Divide and Conquer，DAC）是两种关键的算法设计技巧。本章节将对这两种策略进行概述，为后续章节中对它们的深入探讨奠定基础。

动态规划是解决多阶段决策过程优化问题的一种方法，其核心思想在于将问题分解为相互重叠的子问题，并通过存储这些子问题的解来避免重复计算，最终得到原问题的最优解。与分治策略不同，动态规划特别适用于那些子问题重叠的情况，即子问题的解被多次使用。

分治策略则是一种将大问题分解为小问题的通用解决方法，它将原问题划分为两个或多个规模较小的相同问题，并递归求解这些子问题，最后合并子问题的解以得到原问题的解。分治策略的关键在于分而治之，每个子问题都是独立的。

通过本章的学习，你将了解动态规划与分治策略的基本概念、适用场景以及它们如何互相影响，为更深入地掌握算法原理和实现技巧打下坚实的基础。

# 2. 理解动态规划

## 2.1 动态规划基础理论

### 2.1.1 动态规划的定义和原理

动态规划是一种用于解决复杂问题的算法策略，它将一个复杂问题分解为相对简单的子问题，并将子问题的解存储起来，避免重复计算。其核心是将问题的状态以一种高效的方式存储，并通过状态转移方程来逐步逼近最终解。

动态规划可以应用于具有以下两个性质的问题：
1. **最优子结构（Optimal Substructure）**：一个问题的最优解包含了其子问题的最优解。
2. **重叠子问题（Overlapping Subproblems）**：在解决一个问题的过程中，相同的子问题会被多次计算。

动态规划与分治、贪心算法的主要区别在于：分治算法将问题分解为独立的子问题并同时解决，贪心算法则每一步都做出在当前看来最好的选择，而动态规划则考虑了子问题之间的相互影响，并利用这些影响来找到最终解。

### 2.1.2 动态规划与分治、贪心算法的区别

分治策略将问题拆分为独立子问题后，递归求解这些子问题，然后将它们的解合并起来解决原问题。典型的例子有归并排序和快速排序。相比之下，动态规划维持了一个状态表，每个子问题的解都存储在表中，以避免重复计算。

贪心算法则着眼于当前步骤的选择，认为局部最优可以导致全局最优解，这在许多问题中并不适用。动态规划通过全局状态转移，找到全局最优解。

## 2.2 动态规划的关键要素

### 2.2.1 状态定义和转移方程

在动态规划中，状态是对问题某一阶段的描述。通常，动态规划问题的解决方案依赖于找到合适的**状态表示**和**状态转移方程**。

状态表示一般需要做到：
- 足够用于计算最终结果
- 保证可以使用子问题的解推导出解

而状态转移方程描述了如何从一个或多个子状态推导出当前状态的值。

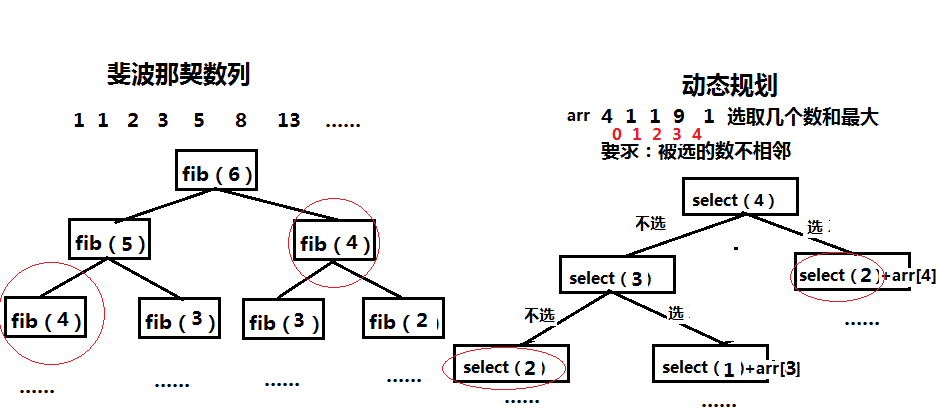
举一个经典的例子：斐波那契数列。
- 状态定义：F(n)表示第n个斐波那契数。
- 状态转移方程：F(n) = F(n-1) + F(n-2)，对于n>2。

### 2.2.2 边界条件和初始值设置

动态规划问题的解决方案还需要定义边界条件和初始值。边界条件是不需要任何计算就能直接得到的状态值。对于斐波那契数列，边界条件是F(0) = 0和F(1) = 1。

初始值的设置对于动态规划的正确性和效率至关重要。在实际编码中，初始值的设置需要确保算法能够正确地遍历所有必要的状态。

### 2.2.3 最优子结构和无后效性

最优子结构是指一个问题的最优解包含其子问题的最优解。这是动态规划可行性的基础。

无后效性是指一个状态的当前值只由它的前一个状态决定，不依赖于其它路径。这个性质保证了动态规划算法的正确性，使得算法可以使用已计算出的状态值来推导出其他状态。

## 2.3 动态规划的算法实现

### 2.3.1 自顶向下（记忆化搜索）

自顶向下方法也称为记忆化搜索，它从最大规模的问题开始，递归求解子问题，并将已经解决的子问题存储起来，以便后续可以直接利用而不需要重新计算。

以下是自顶向下实现斐波那契数列的Python代码：

# 斐波那契数列 - 自顶向下（记忆化搜索）
def fib(n, memo={}):
    if n in memo:
        return memo[n]
    if n == 0:
        return 0
    elif n == 1:
        return 1
    memo[n] = fib(n-1, memo) + fib(n-2, memo)
    return memo[n]

print(fib(10))

在这段代码中，我们使用了一个字典`memo`来存储已经计算过的斐波那契数。这是典型的动态规划实现方式，通过记忆化避免重复计算。

### 2.3.2 自底向上（动态规划表格）

自底向上方法也称为动态规划表格法，它从最小规模的问题开始，逐步构建解，直到得到原问题的解。这种方法通常需要一个表格（数组）来存储子问题的解。

以下是使用自底向上方法实现斐波那契数列的Python代码：

# 斐波那契数列 - 自底向上（动态规划表格）
def fib_bottom_up(n):
    dp = [0] * (n+1)
    dp[0] = 0
    dp[1] = 1
    for i in range(2, n+1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

print(fib_bottom_up(10))

在这段代码中，我们使用了一个数组`dp`来存储斐波那契数列的每一个值。`dp[i]`代表了`F(i)`的值，通过迭代的方式逐步构建出整个数列。

通过本章节的介绍，我们可以理解动态规划的关键要素，包括状态定义、转移方程、边界条件、初始值以及最优子结构和无后效性的概念。同时，我们也掌握了动态规划的两种实现方法：自顶向下的记忆化搜索和自底向上的动态规划表格法。这些基础理论和实现方法为我们在实际问题中应用动态规划提供了坚实的基础。

# 3. 分治策略在动态规划中的应用

## 3.1 分治策略的基本概念
### 3.1.1 分治法的原理和应用场景
分治法是一种在计算机科学和数学中广泛使用的算法设计范式。其核心思想是将一个难以直接解决的大问题，分解成一些规模较小的相同问题，递归地解决这些子问题，然后再合并其结果，以得到原问题的解。

分治法的原理可概括为三个步骤：
1. **分解**：将原问题分解为若干规模较小的子问题。
2. **解决**：递归解决各个子问题。如果子问题足够小，则直接求解。
3. **合并**：将子问题的解合并成原问题的解。

分治策略的应用场景包括但不限于：
- 归并排序（Merge Sort）算法是分治法最典型的例子。
- 快速排序（Quick Sort）也采用了分治的思想。
- 在解决某些几何问题，如最近点对问题时，分治法也可以发挥其优势。
- 分析复杂数据结构的性质，例如在使用快速傅立叶变换（Fast Fourier Transform, FFT）进行大整数乘法时。

分治法的一个重要考量是子问题的分解是否能够有效减少问题的规模，并保证解的合并过程相对简单。因此，在设计分治算法时，需要仔细考虑如何划分问题以及如何有效地合并解。

### 3.1.2 分治与动态规划结合的基本思路
在动态规划问题中，分治策略可以用来加速寻找最优子结构的过程。分治的基本思路可以和动态规划相结合，特别是在那些可以将大问题分解为互相独立或相对独立子问题的场景下。

分治与动态规划结合的思路通常有以下步骤：
1. **问题分解**：首先将原问题根据某种规则分解为若干子问题。子问题的选择是关键，它们应当更容易解决，同时又要保持足够的信息以方便最终问题的求解。
2. **子问题解决**：使用动态规划的方法递归地解决这些子问题。这可能涉及到子问题的进一步分解，直到达到简单到可以直接求解的情况。
3. **信息合并**：利用子问题的解，通过某种策略合并信息以求解原问题。

结合分治策略的动态规划通常能够在某些问题上提供更好的性能，尤其是当动态规划的标准表格方法或记忆化搜索方法在时间或空间复杂度上存在瓶颈时。然而，找到合适的分解方法和合并策略是设计这些算法时的主要挑战。

## 3.2 分治与动态规划的实例解析
### 3.2.1 经典分治问题与动态规划的结合
让我们以一个经典的分治问题——归并排序为例，展示如何将其与动态规划结合。

在归并排序算法中，我们将数组分为两半，对每个子数组递归地进行排序，然后将排序后的子数组合并。这个合并过程实质上就是动态规划中的信息合并阶段。在动态规划中，合并操作类似于构建最优解的过程。

**实现归并排序的Python代码如下：**

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])