【Python数据结构与算法进阶】：从零基础到算法思维构建必学技巧

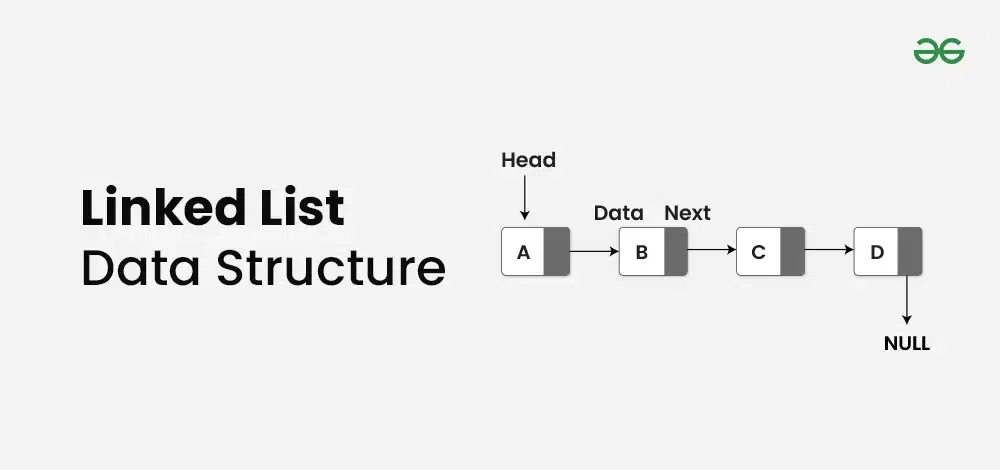
# 1. Python编程基础回顾

Python语言自从20世纪90年代初诞生以来，已经成为全球最受欢迎的编程语言之一。它不仅简洁易读，而且功能强大，应用领域广泛，包括Web开发、数据分析、人工智能等。本章节将重点回顾Python的基础知识，为之后深入探讨数据结构和算法打下坚实的基础。

## 1.1 Python语法基础
Python的语法非常接近英语，易于学习，尤其适合初学者。本节将复习变量定义、数据类型（包括整型、浮点型、字符串、布尔型）、以及控制流（如if-else、for和while循环）等基础知识。理解这些基础知识对后续章节的内容至关重要。

## 1.2 函数和模块使用
函数是组织好的、可重复使用的代码块，用于执行特定任务。Python中定义函数使用关键字`def`，而模块则是一种组织Python代码的方式，其中可以包含函数定义、变量和类等。本节将详细介绍如何定义和使用函数，以及如何导入和使用Python标准库中的模块。

## 1.3 面向对象编程基础
面向对象编程（OOP）是一种编程范式，Python作为一门支持OOP的语言，提供了类和对象来支持面向对象编程。本节将解释类和对象的概念，以及封装、继承、多态等OOP的基本原则。掌握这些概念对于理解和实现更复杂的数据结构和算法非常重要。

通过以上几个小节的回顾，我们可以确保读者对Python的基础知识有一个全面的理解，为后面深入学习数据结构和算法做好充分的准备。

# 2. 数据结构深入解析

## 2.1 基本数据结构

### 2.1.1 列表、元组、字典和集合的特点与用法

Python 提供了多种内置的数据结构，每一种都有其独特的特性和适用场景。列表（List）是一种有序的集合，可以随时添加和删除其中的元素。元组（Tuple）则是一种不可变的有序列表，适用于存储一个固定大小的异构数据集。字典（Dictionary）是一种通过键值对（key-value pairs）存储数据的数据结构，适用于需要通过键快速访问数据的场景。集合（Set）则是一个无序的不重复元素集，适合于执行成员关系测试和消除重复元素。

在实际应用中，选择合适的数据结构将直接影响程序的性能。例如，在需要频繁修改数据集时，使用列表或集合是较好的选择。若数据集大小固定且需要保证元素的唯一性，元组或集合是理想的选择。字典则适合于需要快速查找和关联数据的场景。

### 2.1.2 数据结构的选择依据和应用场景

在选择数据结构时，需考虑以下几个因素：

- 数据类型和大小：数据结构应能高效地支持数据类型并能适应数据规模。
- 数据操作：包括访问、插入、删除和查找等操作的频率和效率。
- 内存使用：数据结构使用的内存是否与数据大小成线性关系。
- 实现复杂度：从代码可读性和维护性角度考虑，应尽量选择简单直观的数据结构。

例如，当需要频繁地进行元素的增加和删除操作时，列表和集合可能是较好的选择。而如果需要快速检索数据，字典的使用可能更为高效。元组则适用于只需要一次性读取且无需修改数据的场景。

## 2.2 高级数据结构

### 2.2.1 栈、队列、堆和树的概念与实现

除了基本的数据结构外，高级数据结构在处理复杂数据问题时显得尤为重要。

- 栈（Stack）是一种后进先出（LIFO）的数据结构。在Python中，列表的append()和pop()方法可以用来实现栈的功能。

# Python 栈的实现
stack = []
stack.append(1)
stack.append(2)
print(stack.pop())  # 输出: 2

- 队列（Queue）是一种先进先出（FIFO）的数据结构，列表的insert()和pop()方法可以模拟队列的操作，但效率不高。使用collections.deque可以更高效地实现队列。

from collections import deque
queue = deque()
queue.append(1)
queue.append(2)
print(queue.popleft())  # 输出: 1

- 堆（Heap）是一种特殊的完全二叉树，Python的heapq模块提供了对堆的支持。堆通常用于实现优先队列。

import heapq
heap = [5, 7, 9, 1, 3]
heapq.heapify(heap)
print(heapq.heappop(heap))  # 输出: 1

- 树（Tree）是由n（n≥0）个节点组成的有限集合，每个节点有0个或多个子节点。树的实现和应用在算法设计中非常重要，尤其是在处理层次化数据和实现高效搜索操作时。

### 2.2.2 字符串与文件的高级操作技巧

字符串和文件操作在处理大量文本数据时非常有用。Python提供了丰富的方法来操作字符串和读写文件。

- 字符串操作技巧中，常见的方法包括字符串拼接、分割、替换等。使用join()方法可以有效地拼接字符串序列，split()方法则用于根据特定分隔符分割字符串。replace()方法可以替换字符串中的子串。

# 字符串拼接
a = "Hello"
b = "World"
result = " ".join([a, b])  # 使用空格分隔
print(result)  # 输出: Hello World

# 字符串分割
text = "apple,banana,cherry"
fruits = text.split(',')  # 按逗号分隔
print(fruits)  # 输出: ['apple', 'banana', 'cherry']

# 字符串替换
original_text = "I like apples"
modified_text = original_text.replace("apples", "oranges")
print(modified_text)  # 输出: I like oranges

- 文件操作涉及到读取和写入数据。Python的open()函数用于打开文件，读写模式（'r', 'w', 'a'）确定了文件的操作方式。文件操作是数据持久化的重要手段。

# 文件读写操作
with open("example.txt", "w") as ***
    ***"Hello, Python!\n")

with open("example.txt", "r") as ***
    ***
    *** 输出: Hello, Python!

## 2.3 数据结构的算法效率分析

### 2.3.1 时间复杂度与空间复杂度

算法效率分析的核心是时间复杂度和空间复杂度。

- 时间复杂度是衡量算法执行时间的相对量度。它通常表示为一个函数，描述了算法执行时间与输入数据大小之间的关系。
- 空间复杂度则是衡量算法在运行过程中临时占用存储空间大小的相对量度。

二者都是以最坏情况下的计算步数来定义的。常见的复杂度类型有O(1)（常数时间复杂度）、O(log n)（对数时间复杂度）、O(n)（线性时间复杂度）、O(n log n)（线性对数时间复杂度）、O(n^2)（平方时间复杂度）等。

### 2.3.2 常见操作的时间复杂度对比

不同操作在不同的数据结构上的时间复杂度有所不同。

- 在列表中访问一个元素的操作是O(1)，而在列表中插入一个元素在最坏情况下的时间复杂度是O(n)。
- 字典提供了O(1)的平均时间复杂度来访问一个元素，这比使用列表访问更快。
- 栈和队列的操作通常有O(1)的时间复杂度。
- 二叉树的搜索操作具有O(log n)的时间复杂度，而在未排序的列表中搜索则需要O(n)的时间复杂度。

理解这些复杂度对比可以帮助我们在面对不同问题时选择更合适的数据结构和算法。

# 3. 算法思想的掌握与应用

## 3.1 算法基础概念

### 3.1.1 算法的定义、特性及其重要性

算法是解决特定问题的一系列定义明确的计算步骤，可以视为一组规则，用于完成任务或达到某种目的。算法的定义可围绕以下几个特性进行阐述：

- **有限性**：算法中的步骤数量是有限的。
- **明确性**：算法中的每一步骤都是明确且无歧义的。
- **输入**：算法具有零个或多个输入。
- **输出**：算法至少有一个输出。
- **有效性**：算法的每一步骤必须足够基本，可以被精确地执行。

算法的重要性体现在其能够为复杂问题提供高效且可靠的解决方案。在计算机科学中，算法是构建软件和系统的基础。良好的算法不仅能够提高代码的执行效率，还能够减少资源消耗，从而在实际应用中产生巨大的经济价值。

### 3.1.2 常见算法问题类型和解题步骤

常见的算法问题类型包括但不限于：

- **排序问题**：将一组数据按照特定顺序排列。
- **搜索问题**：在一组数据中查找特定项。
- **优化问题**：寻找最优解，如旅行商问题。
- **图论问题**：涉及图的遍历、连接性、最短路径等。
- **组合问题**：涉及组合数学，如排列组合、子集和等。

解题步骤通常包括以下几点：

- **问题分析**：理解并清晰定义问题。
- **解决方案**：提出多个可能的解决方案。
- **算法设计**：选择合适的算法设计方法（如贪心、动态规划、回溯等）。
- **复杂度分析**：估计算法的时间复杂度和空间复杂度。
- **编码实现**：将算法逻辑转化为可执行的代码。
- **测试验证**：对算法进行测试，确保其正确性和效率。

## 3.2 常用算法策略

### 3.2.1 分治算法、动态规划与贪心算法

这些策略是解决复杂问题的高级算法思想，每一个都对应着一类特定的问题：

- **分治算法**：将一个复杂的问题分解成两个或多个同类的子问题，解决这些子问题后再合并结果。例如，归并排序和快速排序都是基于分治思想。
下面是归并排序的一个简单实现：

  def merge_sort(arr):
      if len(arr) <= 1:
          return arr
      # 分割数组
      mid = len(arr) // 2
      left_half = merge_sort(arr[:mid])
      right_half = merge_sort(arr[mid:])
      # 合并排序后的子数组
      return merge(left_half, right_half)
  def merge(left, right):
      result = []
      while left and right:
          if left[0] <= right[0]:
              result.append(left.pop(0))
          else:
              result.append(right.pop(0))
      result.extend(left or right)
      return result

  arr = [3, 1, 4, 1, 5, 9, 2, 6]
  sorted_arr = merge_sort(arr)
  print(sorted_arr)

- **动态规划**：将复杂问题分解为简单子问题，并存储这些子问题的解以避免重复计算。动态规划常用于最优化问题，如背包问题。

- **贪心算法**：在对问题求解时，总是做出在当前看来是最好的选择。这意味着它并不从整体最优解出发，因此有可能得到非全局最优解。

### 3.2.2 回溯法和分支限界法

- **回溯法**：通过递归来逐个探索问题的所有可能解。在找到一个解时，如果这个解要通过继续递归求解能够改进，则继续递归下去，否则就回溯到上一步寻找其他可能的解。经典的回溯算法例子有八皇后问题和迷宫求解。

- **分支限界法**：在回溯的基础上，加入剪枝操作以减少搜索空间。分支限界法一般用于求解优化问题，如旅行商问题。

## 3.3 算法的实战演练

### 3.3.1 实际案例分析与代码实现

实际案例分析是将理论知识转化为实践能力的关键步骤。例如，我们可以考虑一个典型的算法问题——最小生成树问题。一个广泛使用的算法是Prim算法，它从任意一个顶点开始构建最小生成树，并不断选择连接已选顶点与未选顶点中权重最小的边。

以下是使用Prim算法的一个代码示例，我们用一个简单的图来表示顶点和它们之间的权重：

import heapq

def prim(graph):
    selected = set()  # 已选择的顶点
    edge_heap = [(0, 'A', 'A')]  # (边的权重, 起点, 终点)，用堆存储边
    mst_weight = 0  # 最小生成树的总权重

    while edge_heap:
        weight, start, end = heapq.heappop(edge_heap)
        if end not in selected:
            selected.add(end)
            mst_weight += weight
            for next_node, next_weight in graph[end].items():
                if next_node not in selected:
                    heapq.heappush(edge_heap, (next_weight, end, next_node))
    return mst_weight

graph = {
    'A': {'B': 2, 'C': 3},
    'B': {'A': 2, 'C': 1, 'D': 1, 'E': 4},
    'C': {'A': 3, 'B': 1, 'F': 5},
    'D': {'B': 1, 'E': 3},
    'E': {'B': 4, 'D': 3, 'F': 1},
    'F': {'C': 5, 'E': 1}
}

print(prim(graph))  # 输出最小生成树的总权重

### 3.3.2 算法面试题的解题思路与技巧

算法面试题通常要求在有限的时间内解决具有挑战性的问题，展示解题思路和技巧尤为重要。面试官不仅关注最终的答案，而且更看重解题的过程和思路。一些常见的解题技巧包括：

- **问题分解**：将复杂问题分解为若干子问题。
- **边界条件**：清晰定义算法的边界条件。
- **问题转化**：将问题转化为已知问题来解决。
- **绘图分析**：通过图示来帮助理解问题和寻找解题思路。
- **代码优化**：编写清晰、高效的代码，注意性能和内存的优化。

在面试中，如果遇到自己不太熟悉的算法问题，可以通过提出问题来引导思路，展示自己的思维过程。同时，对所使用的算法给出时间复杂度和空间复杂度的分析，说明其优势和可能的改进方向。

# 4. Python中的算法实现

## 4.1 排序与搜索算法

### 4.1.1 各类排序算法的原理与Python实现

排序算法是算法学习中不可或缺的一部分，它在计算机科学与工程领域有着广泛的应用。在Python中，我们可以利用内建的排序方法，也可以通过自定义函数来实现各种排序算法。

常见的排序算法有冒泡排序、选择排序、插入排序、快速排序、归并排序等。下面我们将一一了解它们的原理，并提供Python实现。

#### 冒泡排序
冒泡排序的基本思想是通过重复遍历待排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行的，直到没有再需要交换的元素为止。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

# 测试代码
arr = [64, 34, 25, 12, 22, 11, 90]
sorted_arr = bubble_sort(arr)
print("Sorted array is:", sorted_arr)

#### 快速排序
快速排序使用分治法策略来把一个序列分为较小和较大的两个子序列，然后递归地排序两个子序列。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        less = [x for x in arr[1:] if x <= pivot]
        greater = [x for x in arr[1:] if x > pivot]
    return quick_sort(less) + [pivot] + quick_sort(greater)

# 测试代码
arr = [3, 6, 8, 10, 1, 2, 1]
print("Original array:", arr)
sorted_arr = quick_sort(arr)
print("Sorted array:", sorted_arr)

### 4.1.2 搜索算法及其应用

搜索算法的目标是在一个数据结构中找到特定元素的位置。与排序算法类似，搜索算法也是算法学习的核心内容之一。

#### 顺序搜索
最简单的搜索方法就是顺序搜索，它在未排序的列表中逐个检查每个元素直到找到所需的特定项。

def sequential_search(arr, item):
    pos = -1
    for i in range(len(arr)):
        if arr[i] == item:
            pos = i
            break
    return pos

# 测试代码
arr = [5, 10, 15, 20, 25, 30, 35]
item = 25
print(f"Sequential search for {item} found at index {sequential_search(arr, item)}")

#### 二分搜索
二分搜索算法要求被搜索的数据结构已排序。其基本思想是，首先将目标值与序列的中间元素进行比较，如果目标值与中间元素的相等，则搜索成功；如果目标值小于中间元素，则在左半边序列中继续搜索；如果目标值大于中间元素，则在右半边序列中继续搜索。

def binary_search(arr, item):
    low = 0
    high = len(arr)-1
    while low <= high:
        mid = (low + high) // 2
        guess = arr[mid]
        if guess == item:
            return mid
        if guess > item:
            high = mid - 1
        else:
            low = mid + 1
    return -1

# 测试代码
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
item = 4
print(f"Binary search for {item} found at index {binary_search(arr, item)}")

### 4.2 图算法与网络流

图算法是算法学习的一个重要分支，而网络流问题是一个经典且非常有用的图算法问题。其目的是找到在给定的网络中流的最大量。

#### 图的基本概念和遍历算法

图是由顶点的有穷非空集合和顶点之间边的集合组成。图中顶点通常被称为节点，边通常称为连接节点的弧。

遍历算法主要有深度优先搜索（DFS）和广度优先搜索（BFS）。

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for next in graph[start] - visited:
        dfs(graph, next, visited)
    return visited

# 示例图
graph = {'A': set(['B', 'C']),
         'B': set(['A', 'D', 'E']),
         'C': set(['A', 'F']),
         'D': set(['B']),
         'E': set(['B', 'F']),
         'F': set(['C', 'E'])}
visited = dfs(graph, 'A')
print("Visited nodes:", visited)

#### 网络流问题与算法解法

网络流问题通常可以用最大流算法来解决。最大流问题是指在一个网络中，要找出某源点到汇点的最大流量。

Ford-Fulkerson方法是解决最大流问题的一个经典算法，其基本思想是不断地在残余网络中找到一条增广路，然后沿着这条增广路增加流量，直到不能再找到增广路为止。

def ford_fulkerson(graph, source, sink):
    path = find_path(graph, source, sink)
    while path:
        bottleneck = min([graph[u][v] for u, v in zip(path, path[1:])])
        for u, v in zip(path, path[1:]):
            graph[u][v] -= bottleneck
            graph[v][u] += bottleneck
        path = find_path(graph, source, sink)
    return total_flow

# 辅助函数，用于找到增广路
def find_path(graph, source, sink):
    # ... 实现细节略 ...
    return path  # 返回从source到sink的路径

# 测试代码
graph = ...  # 图的构建代码
source = ... # 源点
sink = ...   # 汇点
max_flow = ford_fulkerson(graph, source, sink)
print(f"The maximum flow is: {max_flow}")

### 4.3 字符串匹配与模式识别

字符串匹配是计算机科学中的一个基本问题，它的目的是在一个文本串S内查找一个词W的出现位置。而模式识别关注的是对特定模式的数据进行分析、分类和理解。

#### 字符串处理技巧与KMP算法

KMP（Knuth-Morris-Pratt）算法是一种高效的字符串匹配算法，其基本思想是当出现不匹配时，它能利用已经部分匹配的有效信息，将模式串向右滑动更长的距离，继续进行匹配。

def kmp_table(pattern):
    # 构建KMP的部分匹配表
    table = [0] * len(pattern)
    j = 0
    for i in range(1, len(pattern)):
        while j > 0 and pattern[j] != pattern[i]:
            j = table[j-1]
        if pattern[j] == pattern[i]:
            j += 1
        table[i] = j
    return table

def kmp_search(s, pattern):
    table = kmp_table(pattern)
    j = 0
    for i in range(len(s)):
        while j > 0 and s[i] != pattern[j]:
            j = table[j-1]
        if s[i] == pattern[j]:
            j += 1
        if j == len(pattern):
            return i - j + 1
    return -1

# 测试代码
s = "ABC ABCDAB ABCDABCDABDE"
pattern = "ABCDABD"
print("Text:", s)
print("Pattern:", pattern)
print("KMP Search index:", kmp_search(s, pattern))

#### 正则表达式与模式匹配的高级应用

正则表达式（Regular Expression）是一种文本模式匹配工具，它定义了复杂的文本模式，用于文本搜索、替换等操作。

import re

def regex_match(text, pattern):
    # 使用Python的re模块进行正则表达式匹配
    match = re.match(pattern, text)
    if match:
        print(f"Pattern {pattern} matches at index {match.start()}")
    else:
        print(f"Pattern {pattern} does not match.")

# 测试代码
text = "The rain in Spain"
pattern = r"([A-Z][a-z]*)\s+([A-Z][a-z]*)"
regex_match(text, pattern)

## 总结

在第四章中，我们深入探讨了Python中的算法实现，涵盖了排序与搜索算法、图算法与网络流问题、以及字符串匹配与模式识别。我们学习了各类排序和搜索算法的原理，并通过Python代码实现了冒泡排序、快速排序、顺序搜索和二分搜索。同时，我们对图算法进行了初步探索，包括图的基本概念、遍历算法、网络流问题及解决算法。在字符串匹配部分，我们通过KMP算法和正则表达式展示了如何高效地处理字符串模式匹配问题。这些算法是数据结构与算法应用的核心，并在实际开发中发挥重要作用。

# 5. 数据结构与算法的实际案例分析

## 5.1 实际问题的数据结构选择

在解决复杂问题时，选择合适的数据结构对于提高效率和实现优化至关重要。本章节将深入探讨在不同问题场景下，如何选择合适的数据结构，并对其进行优化。

### 5.1.1 数据量大时的结构选择和优化

当处理大量数据时，数据结构的选择对于性能的影响尤为显著。以社交媒体平台的用户信息存储为例，这里将探讨在数据量大时如何选择和优化数据结构。

首先，当数据量达到亿级时，关系型数据库（如MySQL）可能会遇到性能瓶颈。这时，可以考虑使用NoSQL数据库如MongoDB，它提供了更灵活的文档存储模型，能够更高效地处理大数据。

其次，为了进一步优化性能，可以将数据结构的选择与具体的应用场景结合起来。例如，如果需要处理大量读写操作，可以使用哈希表（HashMap）进行优化，因为哈希表提供了平均常数时间复杂度（O(1)）的查找、插入和删除操作。

下面是使用Python中字典（实现了哈希表的数据结构）进行数据快速存取的代码示例：

# 示例代码：使用字典进行数据快速存取
user_data = {}
def update_user_data(user_id, data):
    user_data[user_id] = data  # O(1)的时间复杂度

def get_user_data(user_id):
    return user_data.get(user_id)  # O(1)的时间复杂度

### 5.1.2 问题复杂度分析与结构适用性评估

问题复杂度的分析对于选择合适的数据结构至关重要。例如，在处理网络请求时，如果需要频繁地查找最近的操作记录，可以考虑使用平衡二叉树（如红黑树），因为它可以在对数时间内完成查找、插入和删除操作。

以下是一个平衡二叉树的实现示例，并展示了如何进行基本操作：

# 示例代码：平衡二叉树的节点定义和基本操作
class Node:
    def __init__(self, key, val):
        self.key = key
        self.val = val
        self.left = None
        self.right = None
        self.height = 1  # 初始高度

class AVLTree:
    def insert(self, root, key, val):
        # 递归插入节点并更新高度
        pass
        # 重新平衡树并返回根节点
        pass
    def search(self, root, key):
        # O(log n)时间复杂度内查找节点
        pass

在设计系统时，除了时间复杂度之外，空间复杂度也是需要考虑的因素。例如，如果系统对内存消耗有严格限制，可以考虑使用链表代替数组来减少内存占用。

## 5.2 算法在项目中的应用

在软件开发过程中，算法不仅用于解决理论问题，更是解决实际问题的利器。本节将通过两个案例分析，展示排序算法和搜索算法在项目中的具体应用。

### 5.2.1 项目案例分析：排序算法的应用

在电子商务平台上，商品价格排序是常见的需求。为了应对不同的排序需求（如按价格升序或降序），可以使用快速排序、归并排序等高效的排序算法。

例如，使用Python的内置排序方法`sorted()`对商品列表进行排序：

# 示例代码：使用内置排序方法对商品列表进行排序
def sort_products_by_price(products):
    return sorted(products, key=lambda product: product['price'])

在某些情况下，为了实现更高效的排序，可以结合具体的数据分布特点选择合适的算法。例如，当数据量非常大时，可以考虑使用外部排序或并行排序。

### 5.2.2 项目案例分析：搜索算法的应用

在在线教育平台中，查找课程资源是一项核心功能。为了提高查找效率，可以采用二分搜索算法或哈希表搜索。

例如，当课程资源按难度排序后，可以使用二分搜索快速定位用户请求的课程：

# 示例代码：使用二分搜索算法快速定位课程
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

在实践中，搜索算法的选择往往需要结合数据的存储方式和访问模式。例如，在数据库中进行文本搜索时，可以使用索引结构来加速查找。

## 5.3 优化思路与技巧分享

针对数据结构和算法的优化，不仅可以通过选择更高效的数据结构和算法实现，还可以在代码层面和系统层面上进一步优化。

### 5.3.1 代码层面的优化策略

在代码层面，优化可以从减少不必要的数据结构操作和选择合适的数据结构两个方面入手。

例如，如果频繁进行列表的扩展操作，可以使用数组的`append`方法代替列表连接操作，因为后者会创建新的列表并复制元素：

# 示例代码：优化列表扩展操作
items = []
for item in new_items:
    items.append(item)  # O(1)的平均时间复杂度
    # items += [item]  # 不推荐，会创建新列表并复制元素

在选择数据结构时，如果需要频繁更新集合中的元素，集合（set）操作比列表更快，因为集合在内部通过哈希表实现，提供了更快的查找和更新效率。

### 5.3.2 系统层面的优化方法

在系统层面，优化可以通过并行计算、缓存机制和负载均衡等策略来实现。

例如，在处理大量并发请求时，可以使用多进程或多线程来分散请求负载。Python中的多线程受限于全局解释器锁（GIL），此时可以使用`multiprocessing`模块实现并行处理：

# 示例代码：使用多进程模块实现并行处理
import multiprocessing

def process_data(data):
    # 处理数据
    return result

if __name__ == '__main__':
    data = [...]
    with multiprocessing.Pool(processes=4) as pool:
        results = pool.map(process_data, data)

此外，缓存机制可以显著提高系统性能。通过缓存热点数据，可以避免重复计算，减少数据库的访问压力。在Python中，可以使用`functools.lru_cache`装饰器来实现简单的函数调用缓存：

from functools import lru_cache

@lru_cache(maxsize=128)
def compute_heavy_task(param):
    # 执行复杂的计算任务
    return result

在实际应用中，系统优化可能需要综合多种策略，针对不同问题场景制定个性化解决方案。通过不断的实践和经验积累，开发者可以逐步提升系统性能，优化用户体验。

# 6. 进阶话题与未来展望

随着技术的不断进步，Python在算法竞赛和人工智能领域的应用愈发广泛。掌握进阶话题不仅能够提升我们解决复杂问题的能力，还能够帮助我们洞察数据结构与算法在未来的发展趋势。

## 6.1 Python算法竞赛介绍

### 6.1.1 算法竞赛的意义与准备

算法竞赛如ACM ICPC、Google Code Jam等是测试程序员编程能力的极佳平台。参加算法竞赛不仅能够锻炼选手的思维敏捷度，还能够加深对数据结构和算法的理解。准备过程中，选手需要掌握各类经典算法，并在有限的时间内快速设计出解决方案。此外，熟悉各种在线评测系统的使用也是必不可少的。

### 6.1.2 竞赛中的经典题目与思路

在算法竞赛中，通常会遇到如下几个领域的经典题目：

- 动态规划：经常用于解决优化问题，例如找零钱问题、背包问题。
- 图论：图的遍历和最短路径问题，如Dijkstra算法、Floyd算法。
- 数学问题：组合数学、数论等领域的应用，例如素数筛选、组合数计算。

针对这些经典题目，解题思路通常包括：

- 定义状态：明确问题的状态表示，如DP中的子问题。
- 状态转移：分析状态之间的转换关系。
- 边界条件：处理初始状态和结束状态。
- 计算方法：确定最优子结构，应用贪心、动态规划等方法。

## 6.2 人工智能中的数据结构与算法

### 6.2.1 机器学习的算法基础

机器学习中数据结构和算法的应用主要体现在模型构建和数据处理上。树结构如决策树、随机森林在分类和回归问题中有着广泛的应用。而图结构的深度神经网络则在图像识别和自然语言处理领域展现了强大的能力。此外，数据预处理和特征工程中，高效的数据结构如哈希表、堆结构、并查集等也是不可或缺的。

### 6.2.2 深度学习中的数据结构应用

在深度学习中，算法的高效性往往依赖于特定的数据结构。例如，卷积神经网络（CNN）中的卷积操作可以视为一种特殊的乘法累加操作，它利用了图像数据的空间局部性。循环神经网络（RNN）和长短期记忆网络（LSTM）处理序列数据时，需要考虑时间维度上的连贯性。为了加快计算速度和减少内存消耗，GPU编程中使用了多种数据结构来优化矩阵运算。

## 6.3 未来数据结构与算法的发展趋势

### 6.3.1 新兴技术对数据结构的影响

随着量子计算、边缘计算等新兴技术的发展，传统的数据结构和算法面临着新的挑战与机遇。量子计算机的并行性和概率性为解决某些问题提供了全新的途径。同时，大数据和云计算的兴起也促进了对分布式数据结构和算法的研究，如分布式哈希表（DHT）和一致性哈希等。

### 6.3.2 算法的伦理与社会责任

算法不仅是一门技术，也涉及到伦理和社会责任。在设计和实现算法时，开发者需要考虑算法的公平性、透明度和隐私保护。例如，在机器学习领域，避免算法偏见成为了重要的研究课题。数据结构和算法的设计者应当积极采取措施，确保技术的公正性和有益性。

通过深入分析和讨论进阶话题，我们可以看到数据结构与算法在未来技术发展中的核心地位。无论是参加算法竞赛，还是从事人工智能项目，都需要不断地学习、实践和创新。在这个过程中，我们不仅要追求技术上的突破，还应该关注技术应用背后的社会责任和伦理问题。