【Python排序算法优化】：从基础到高级，实现与优化全攻略

# 1. 排序算法基础与Python实现

排序是计算机科学的核心主题之一，贯穿了软件开发的许多方面。在本章中，我们将探讨排序算法的基础知识，并用Python语言演示它们的实现方法。

## 1.1 排序算法概念
排序算法用于将一系列元素按照一定的顺序（通常是升序或降序）进行排列。它是最基本的计算机操作之一，几乎所有的重要算法和数据处理流程都依赖于排序。

## 1.2 排序算法的分类
排序算法通常分为两类：比较排序和非比较排序。比较排序依赖于比较两个元素的大小，而非比较排序利用元素的其他属性进行排序。比较排序的效率通常受限于比较次数，而非比较排序（如计数排序、基数排序）则不受此限制。

## 1.3 Python中的排序实现
Python提供了一些内置的排序方法，例如列表的`sort()`方法和`sorted()`函数。这些方法内部可以使用高效的排序算法（如Timsort算法），为Python程序提供快速可靠的排序能力。

在接下来的章节中，我们将深入探讨不同类型的排序算法，并通过Python代码示例展示它们的使用和实现过程。我们会关注算法的时间复杂度和空间复杂度，并对它们在不同场景下的表现进行比较分析。

# 示例：Python内置的sorted()函数使用
items = [3, 1, 4, 1, 5, 9]
sorted_items = sorted(items)
print(sorted_items)  # 输出: [1, 1, 3, 4, 5, 9]

通过实际编码和分析，我们不仅能理解排序算法的原理，还能掌握如何高效地应用这些算法解决问题。

# 2. 常见排序算法的Python实现与比较

## 2.1 基础排序算法

### 2.1.1 冒泡排序和选择排序
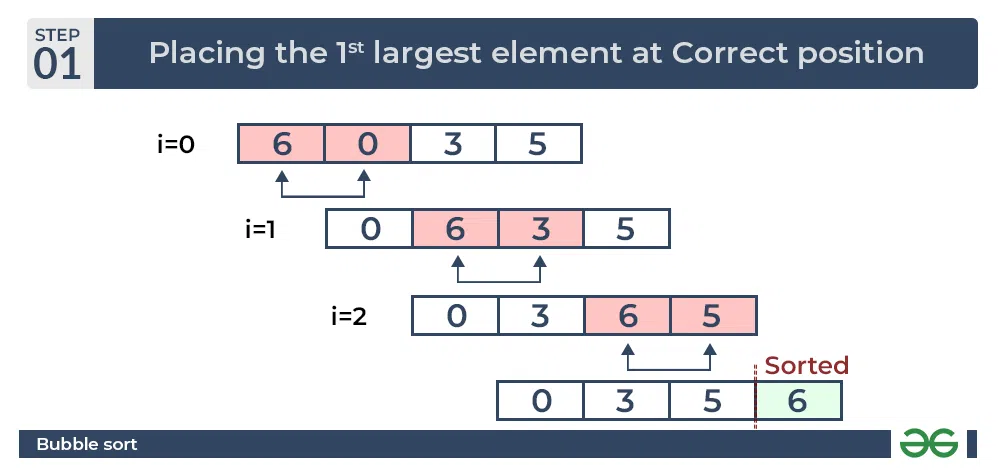
冒泡排序是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。选择排序的基本思想是：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

下面是冒泡排序和选择排序的Python代码示例：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

def selection_sort(arr):
    for i in range(len(arr)):
        min_idx = i
        for j in range(i+1, len(arr)):
            if arr[min_idx] > arr[j]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

在冒泡排序中，我们逐个比较相邻的元素，如果顺序不对就交换它们。选择排序则是在每一次迭代中选择出一个未排序部分的最小值，并将其放在已排序部分的末尾。尽管它们都是简单易懂的排序方法，但效率通常较低。

### 2.1.2 插入排序和归并排序
插入排序的工作方式像是打扑克牌时整理手中的牌，它逐个将未排序的元素插入到已排序的合适位置。归并排序是将已拆分的数列，从最小的单位开始，两两排序合并，不断重复直到整个数列排序完成。

以下是插入排序和归并排序的Python代码实现：

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

插入排序的时间复杂度依赖于数列的初始顺序，最佳情况下（已经有序）的时间复杂度为O(n)，但平均和最坏情况下的时间复杂度为O(n^2)。归并排序无论对于何种情况，都能保持稳定的O(nlogn)时间复杂度。

### 性能对比表格

| 排序算法 | 最佳时间复杂度 | 平均时间复杂度 | 最差时间复杂度 | 空间复杂度 |
|------------|------------|------------|------------|--------|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) |

## 2.2 高级排序算法

### 2.2.1 快速排序和堆排序
快速排序是一种分而治之的算法，通过选择一个元素作为“基准”(pivot)，然后将数组分为两个子数组，所有比基准小的元素放在基准的左边，所有比基准大的元素放在基准的右边，然后递归地对子数组进行快速排序。堆排序利用堆这种数据结构所设计的一种排序算法，它利用了大顶堆或小顶堆的性质来对数据进行排序。

快速排序和堆排序的Python实现代码如下：

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

快速排序的平均时间复杂度为O(nlogn)，但最差情况下的时间复杂度会退化到O(n^2)，这通常发生在每次划分选取的基准都是最大或最小值时。堆排序由于要构建堆，最坏时间复杂度也是O(nlogn)，但能保证整体的时间复杂度稳定在O(nlogn)，这使得它在处理大规模数据时更加可靠。

### 2.2.2 希尔排序和计数排序
希尔排序是一种基于插入排序的快速排序算法，通过将原数据分组进行插入排序，使得数据逐渐变得有序，再进行最终的插入排序。计数排序是一种非比较型排序算法，适用于一定范围内的整数排序，在具体实现时，需要先确定数据的范围，并创建相应大小的计数数组，用来统计每个值出现的次数。

希尔排序和计数排序的Python实现代码如下：

def shell_sort(arr):
    n = len(arr)
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2

def counting_sort(arr, min_value, max_value):
    count = [0] * (max_value - min_value + 1)
    output = [0] * len(arr)