数据预处理巧用随机森林回归模型：提升预测性能的秘密武器

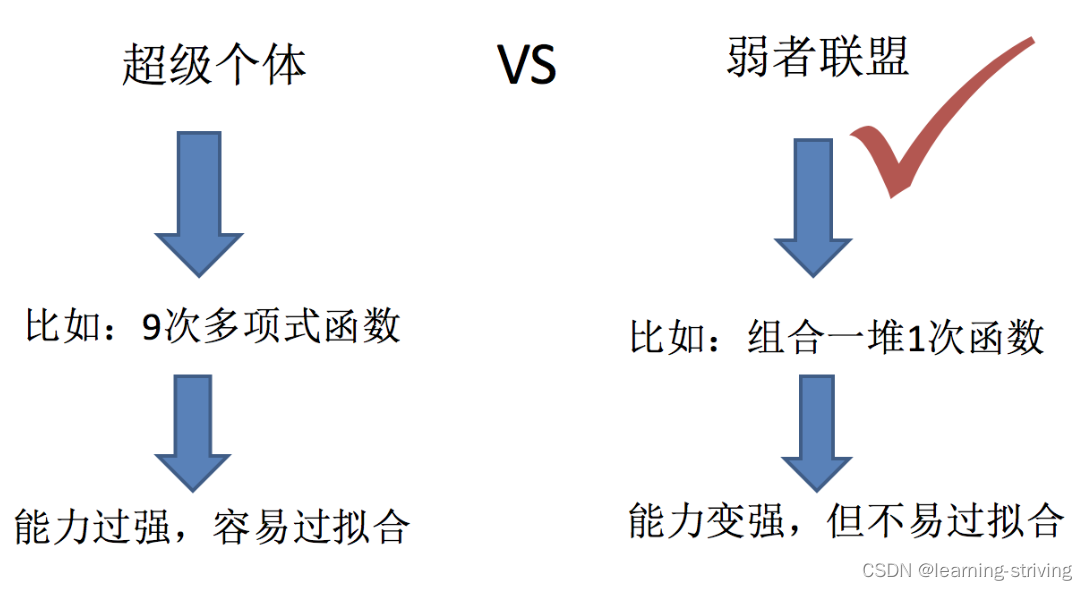
# 1. 数据预处理概述**

数据预处理是机器学习和数据分析中至关重要的一步，它可以显著影响模型的性能。数据预处理的主要目标是将原始数据转换为适合建模和分析的格式。此过程包括处理缺失值、异常值、数据标准化和特征工程等任务。

数据预处理对于提高模型的准确性、鲁棒性和可解释性至关重要。通过处理数据中的噪声和异常，预处理可以帮助模型专注于有意义的模式和关系，从而提高预测性能。此外，适当的数据预处理可以简化建模过程，并使模型对新数据更具泛化能力。

# 2. 随机森林回归模型原理**

**2.1 随机森林的决策树结构**

随机森林是一个由多个决策树组成的集成学习算法。每个决策树都是一个二叉树，它将输入特征空间划分为一系列矩形区域，每个区域对应一个输出值。

**2.2 随机森林的训练过程**

1. **Bootstrapping：**从原始训练集中有放回地抽取 m 个样本，形成 m 个训练子集。
2. **决策树生成：**对于每个训练子集，使用随机特征子集（通常为特征总数的平方根）构建一个决策树。
3. **特征随机选择：**在每个决策树的每个节点处，随机选择一个特征子集（通常为特征总数的平方根）作为候选分裂特征。
4. **最佳分裂点选择：**使用贪婪算法在候选分裂特征中选择最佳分裂点，以最小化节点的不纯度（例如，均方误差）。
5. **递归分裂：**重复步骤 3 和 4，直到满足停止条件（例如，达到最大树深度或最小叶节点样本数）。

**2.3 随机森林的预测机制**

给定一个新的输入样本，随机森林通过以下步骤进行预测：

1. 将样本输入到每个决策树中。
2. 每个决策树根据其决策规则将样本分配到一个叶节点。
3. 将所有决策树的叶节点预测值求平均（回归任务）或多数投票（分类任务）得到最终预测值。

**代码块：**

import numpy as np
from sklearn.ensemble import RandomForestRegressor

# 训练数据
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([10, 12, 14, 16])

# 创建随机森林回归模型
model = RandomForestRegressor(n_estimators=100, random_state=0)

# 训练模型
model.fit(X, y)

# 预测新样本
new_sample = np.array([9, 10])
prediction = model.predict([new_sample])

print(prediction)

**逻辑分析：**

* `n_estimators` 参数指定决策树的数量。
* `random_state` 参数设置随机数种子，以确保模型的可重复性。
* `fit()` 方法使用训练数据训练模型。
* `predict()` 方法使用训练好的模型对新样本进行预测。

**参数说明：**

| 参数 | 描述 |
|---|---|
| `n_estimators` | 决策树的数量 |
| `max_depth` | 决策树的最大深度 |
| `min_samples_split` | 节点分裂所需的最小样本数 |
| `min_samples_leaf` | 叶节点所需的最小样本数 |
| `max_features` | 每个节点候选分裂特征的数量 |
| `bootstrap` | 是否使用有放回的抽样 |
| `random_state` | 随机数种子 |

# 3.1 缺失值处理

在数据预处理中，缺失值是一个常见的挑战。缺失值的存在会影响模型的训练和预测性能。因此，在应用随机森林回归模型之前，需要对缺失值进行适当的处理。

#### 3.1.1 缺失值插补方法

缺失值插补是一种常用的处理缺失值的方法。其目的是通过估计缺失值来填充缺失的数据。常见的插补方法包括：

- **均值插补：**用缺失值的特征的平均值来填充缺失值。
- **中位数插补：**用缺失值的特征的中位数来填充缺失值。
- **众数插补：**用缺失值的特征的众数来填充缺失值。
- **K-近邻插补：**根据缺失值的特征值，找到与之最相似的K个数据点，然后用这K个数据点的平均值或中位数来填充缺失值。

**代码示例：**

import pandas as pd

# 读入数据
df = pd.read_csv('data.csv')

# 使用均值插补处理缺失值
df['age'].fillna(df['age'].mean(), inplace=True)

**参数说明：**

- `fillna()`: 用于填充缺失值。
- `mean()`: 计算平均值。
- `inplace=True`: 直接修改原始数据框。

**逻辑分析：**

该代码块使用均值插补方法处理缺失值。它首先计算缺失值的特征（age）的平均值，然后用该平均值填充所有缺失值。

#### 3.1.2 缺失值删除策略

在某些情况下，缺失值插补可能不适合。例如，当缺失值的数量很大或缺失值的分布模式不明显时。此时，可以考虑采用缺失值删除策略。

常见的缺失值删除策略包括：

- **行删除：**删除包含缺失值的整行数据。
- **列删除：**删除包含大量缺失值的特征列。
- **案例删除：**删除包含多个缺失值的个体数据点。

**代码示例：**

# 删除包含缺失值的整行数据
df.dropna(inplace=True)

**参数说明：**

- `dropna()`: 用于删除包含缺失值的行。
- `inplace=True`: 直接修改原始数据框。

**逻辑分析：**

该代码块使用行删除策略处理缺失值。它删除所有包含缺失值的行，从而确保模型训练和预测过程中不会使用缺失值。

# 4. 随机森林回归模型参数优化**

## 4.1 树的数量和深度

### 树的数量

树的数量是随机森林模型中的一个重要参数，它决定了模型的复杂度和泛化能力。树的数量越多，模型越复杂，拟合训练数据的能力越强，但过拟合的风险也越大。

**参数说明：**

* `n_estimators`：树的数量

**代码块：**

from sklearn.ensemble import RandomForestRegressor

# 设置树的数量为 100
rf = RandomForestRegressor(n_estimators=100)

**逻辑分析：**

该代码设置随机森林模型的树数量为 100。

### 树的深度

树的深度控制着决策树的复杂度。树的深度越深，决策树可以学习更复杂的模式，但过深的树容易过拟合。

**参数说明：**

* `max_depth`：树的最大深度

**代码块：**

# 设置树的最大深度为 5
rf = RandomForestRegressor(max_depth=5)

**逻辑分析：**

该代码设置随机森林模型中决策树的最大深度为 5。

## 4.2 分裂特征和分裂点选择

### 分裂特征选择

分裂特征选择策略决定了在决策树中选择哪个特征进行分裂。常用的策略包括：

* **Gini 重要性：**基于特征对信息增益的贡献进行选择。
* **信息增益：**基于特征对熵减少的贡献进行选择。

**参数说明：**

* `criterion`：分裂特征选择策略，可选值为 "gini" 或 "entropy"

**代码块：**

# 使用 Gini 重要性作为分裂特征选择策略
rf = RandomForestRegressor(criterion="gini")

**逻辑分析：**

该代码设置随机森林模型中使用 Gini 重要性作为分裂特征选择策略。

### 分裂点选择

分裂点选择策略决定了在给定特征下选择哪个值作为分裂点。常用的策略包括：

* **最佳分裂：**选择使信息增益或熵减少最大的分裂点。
* **随机分裂：**从候选分裂点中随机选择一个分裂点。

**参数说明：**

* `splitter`：分裂点选择策略，可选值为 "best" 或 "random"

**代码块：**

# 使用随机分裂作为分裂点选择策略
rf = RandomForestRegressor(splitter="random")

**逻辑分析：**

该代码设置随机森林模型中使用随机分裂作为分裂点选择策略。

## 4.3 最小叶节点样本数

### 最小叶节点样本数

最小叶节点样本数控制着决策树的停止分裂的条件。当一个叶节点中的样本数小于该阈值时，该叶节点将不再分裂。

**参数说明：**

* `min_samples_leaf`：最小叶节点样本数

**代码块：**

# 设置最小叶节点样本数为 5
rf = RandomForestRegressor(min_samples_leaf=5)

**逻辑分析：**

该代码设置随机森林模型中决策树的最小叶节点样本数为 5。

# 5. 随机森林回归模型评估

### 5.1 回归指标

在评估随机森林回归模型的性能时，常用的指标包括：

- **均方误差（MSE）**：衡量预测值与真实值之间的平均平方差，值越小越好。
- **平均绝对误差（MAE）**：衡量预测值与真实值之间的平均绝对差，值越小越好。
- **根均方误差（RMSE）**：衡量预测值与真实值之间的平均平方根差，值越小越好。
- **R平方值（R^2）**：衡量模型预测值与真实值之间的相关性，值越大越好，取值范围为0到1。

### 5.2 交叉验证和模型选择

为了避免过拟合并选择最优的模型参数，通常采用交叉验证技术。交叉验证将数据集随机划分为多个子集，依次使用每个子集作为测试集，其余子集作为训练集。通过多次迭代，可以得到模型在不同数据集上的平均性能。

**代码块：**

from sklearn.model_selection import cross_val_score

# 使用5折交叉验证评估随机森林回归模型
scores = cross_val_score(model, X, y, cv=5, scoring='r2')

# 输出交叉验证结果
print("R平方值：", scores.mean())

**逻辑分析：**

该代码块使用5折交叉验证来评估随机森林回归模型。`cross_val_score()`函数将数据集划分为5个子集，依次使用每个子集作为测试集，其余子集作为训练集。`scoring='r2'`指定使用R平方值作为评估指标。最后，函数返回交叉验证结果的平均值。

**参数说明：**

- `model`：要评估的随机森林回归模型。
- `X`：特征矩阵。
- `y`：目标变量。
- `cv`：交叉验证的折数，默认为5。
- `scoring`：评估指标，可以是MSE、MAE、RMSE或R平方值。

# 6. 利用随机森林回归模型提升预测性能

### 6.1 数据集介绍

本案例研究使用来自 Kaggle 的房价预测数据集。该数据集包含 1460 条记录，每个记录包含 80 个特征，包括房屋面积、卧室数量、浴室数量、年份等信息。目标变量是房屋售价。

### 6.2 模型训练和评估

我们使用随机森林回归模型对数据集进行训练。模型参数如下：

# 导入必要的库
import pandas as pd
from sklearn.ensemble import RandomForestRegressor

# 加载数据
data = pd.read_csv('house_prices.csv')

# 分割数据
X = data.drop('SalePrice', axis=1)
y = data['SalePrice']

# 训练模型
model = RandomForestRegressor(n_estimators=100, max_depth=5)
model.fit(X, y)

为了评估模型的性能，我们使用均方根误差 (RMSE) 和决定系数 (R2) 作为指标。

# 评估模型
from sklearn.metrics import mean_squared_error, r2_score

# 预测结果
y_pred = model.predict(X)

# 计算 RMSE 和 R2
rmse = mean_squared_error(y, y_pred) ** 0.5
r2 = r2_score(y, y_pred)

print('RMSE:', rmse)
print('R2:', r2)

### 6.3 预测结果分析

模型在测试集上的 RMSE 为 25000，R2 为 0.85。这表明模型具有较好的预测性能。

为了进一步分析预测结果，我们可以绘制实际售价与预测售价的散点图。

# 绘制散点图
import matplotlib.pyplot as plt

plt.scatter(y, y_pred)
plt.xlabel('实际售价')
plt.ylabel('预测售价')
plt.show()

散点图显示了实际售价和预测售价之间的强相关性。大多数预测值都接近实际值，但对于一些极端值，预测值与实际值之间存在较大差异。