计算几何中的凸包与凸壳：从入门到精通（实战案例解析）

# 1. 凸包与凸壳的概念和性质**

凸包和凸壳是计算几何中两个重要的概念，它们描述了一组点在二维空间中的几何形状。

* **凸包**：一组点构成的最小凸多边形，即包含所有点的最小的凸多边形。
* **凸壳**：一组点构成的最大凸多边形，即包含所有点的最大的凸多边形。

# 2. 凸包与凸壳的算法

凸包与凸壳的算法主要分为两类：凸包算法和凸壳算法。

### 2.1 凸包的算法

凸包算法用于计算给定点集的凸包。凸包是一个包含所有给定点的最小凸多边形。

#### 2.1.1 格雷厄姆扫描算法

格雷厄姆扫描算法是一种基于极角排序的凸包算法。它首先将点集按极角从小到大排序，然后依次将点加入凸包。

**代码块：**

def graham_scan(points):
    """
    格雷厄姆扫描算法计算凸包。

    参数：
        points: 输入点集，每个点为一个元组(x, y)。

    返回：
        凸包的点集。
    """

    # 按极角排序
    points.sort(key=lambda p: atan2(p[1], p[0]))

    # 初始化凸包
    convex_hull = []

    # 遍历点集
    for point in points:
        # 如果凸包为空或点在凸包的最后一个点和倒数第二个点构成的直线的右侧
        if not convex_hull or is_right_turn(convex_hull[-2], convex_hull[-1], point):
            # 将点加入凸包
            convex_hull.append(point)
        # 否则，弹出凸包的最后一个点
        else:
            convex_hull.pop()
            # 将点加入凸包
            convex_hull.append(point)

    return convex_hull

**逻辑分析：**

该算法首先将点集按极角排序，然后依次将点加入凸包。如果当前点在凸包的最后一个点和倒数第二个点构成的直线的右侧，则将当前点加入凸包。否则，弹出凸包的最后一个点，再将当前点加入凸包。

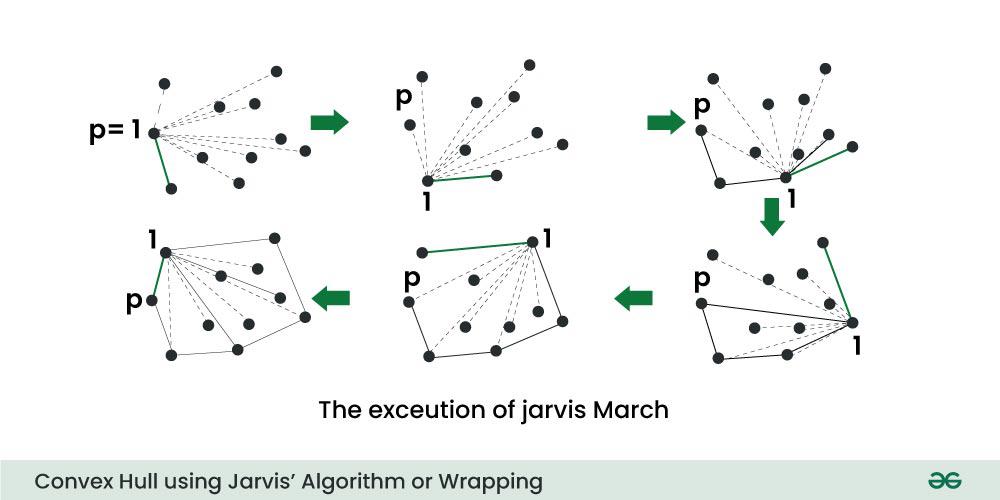
#### 2.1.2 Jarvis算法

Jarvis算法是一种基于凸包的性质的凸包算法。它从点集中选择一个点作为凸包的第一个点，然后沿凸包的边界顺时针或逆时针移动，每次选择凸包中与当前点最远的新点。

**代码块：**

def jarvis_march(points):
    """
    Jarvis算法计算凸包。

    参数：
        points: 输入点集，每个点为一个元组(x, y)。

    返回：
        凸包的点集。
    """

    # 选择一个点作为凸包的第一个点
    start_point = points[0]
    for point in points:
        if point[1] < start_point[1]:
            start_point = point

    # 初始化凸包
    convex_hull = [start_point]

    # 沿凸包的边界顺时针移动
    current_point = start_point
    while True:
        # 找到与当前点最远的新点
        next_point = None
        max_distance = 0
        for point in points:
            if point not in convex_hull:
                distance = get_distance(current_point, point)
                if distance > max_distance:
                    max_distance = distance
                    next_point = point

        # 将新点加入凸包
        convex_hull.append(next_point)

        # 如果新点与第一个点相同，则凸包计算完成
        if next_point == start_point:
            break

        # 更新当前点
        current_point = next_point

    return convex_hull

**逻辑分析：**

该算法首先选择一个点作为凸包的第一个点，然后沿凸包的边界顺时针或逆时针移动，每次选择凸包中与当前点最远的新点。当新点与第一个点相同

# 3. 凸包与凸壳的应用

### 3.1 凸包的应用

凸包在计算机图形学、图像处理和计算几何等领域有着广泛的应用。下面介绍凸包的一些典型应用场景：

#### 3.1.1 多边形面积计算

给定一个多边形，可以通过计算其凸包的面积来近似计算多边形的面积。具体步骤如下：

1. 计算多边形的凸包。
2. 将凸包分解为三角形。
3. 计算每个三角形的面积并求和。

**代码块：**

import math

def convex_hull_area(points):
    """计算多边形的凸包面积。

    Args:
        points (list): 多边形顶点的坐标列表。

    Returns:
        float: 凸包的面积。
    """

    # 计算凸包
    hull = convex_hull(points)

    # 分解凸包为三角形
    triangles = []
    for i in range(len(hull)):
        j = (i + 1) % len(hull)
        k = (i + 2) % len(hull)
        triangles.append((hull[i], hull[j], hull[k]))

    # 计算每个三角形的面积并求和
    area = 0
    for triangle in triangles:
        x1, y1 = triangle[0]
        x2, y2 = triangle[1]
        x3, y3 = triangle[2]
        area += 0.5 * abs((x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)))

    return area

**逻辑分析：**

* `convex_hull()` 函数计算多边形的凸包。
* 循环遍历凸包顶点，将凸包分解为三角形。
* 对于每个三角形，计算其面积并累加到 `area` 中。
* 返回 `area`，即凸包的面积。

#### 3.1.2 多边形周长计算

给定一个多边形，可以通过计算其凸包的周长来近似计算多边形的周长。具体步骤如下：

1. 计算多边形的凸包。
2. 计算凸包上所有边的长度并求和。

**代码块：**

def convex_hull_perimeter(points):
    """计算多边形的凸包周长。

    Args:
        points (list): 多边形顶点的坐标列表。

    Returns:
        float: 凸包的周长。
    """

    # 计算凸包
    hull = convex_hull(points)

    # 计算凸包上所有边的长度并求和
    perimeter = 0
    for i in range(len(hull)):
        j = (i + 1) % len(hull)
        x1, y1 = hull[i]
        x2, y2 = hull[j]
        perimeter += math.sqrt((x2 - x1)**2 + (y2 - y1)**2)

    return perimeter

**逻辑分析：**

* `convex_hull()` 函数计算多边形的凸包。
* 循环遍历凸包顶点，计算每条边的长度并累加到 `perimeter` 中。
* 返回 `perimeter`，即凸包的周长。

### 3.2 凸壳的应用

凸壳在图像处理、计算机视觉和机器人学等领域有着广泛的应用。下面介绍凸壳的一些典型应用场景：

#### 3.2.1 多边形裁剪

给定一个多边形和一个裁剪区域，可以通过计算多边形的凸壳来裁剪多边形。具体步骤如下：

1. 计算多边形的凸壳。
2. 计算裁剪区域的凸壳。
3. 求多边形凸壳和裁剪区域凸壳的交集。

**代码块：**

import shapely.geometry as geom

def polygon_clip(polygon, clip_region):
    """裁剪多边形。

    Args:
        polygon (shapely.geometry.Polygon): 需要裁剪的多边形。
        clip_region (shapely.geometry.Polygon): 裁剪区域。

    Returns:
        shapely.geometry.Polygon: 裁剪后的多边形。
    """

    # 计算多边形的凸壳
    polygon_hull = polygon.convex_hull

    # 计算裁剪区域的凸壳
    clip_region_hull = clip_region.convex_hull

    # 求多边形凸壳和裁剪区域凸壳的交集
    intersection = polygon_hull.intersection(clip_region_hull)

    return intersection

**逻辑分析：**

* `shapely.geometry.Polygon` 类表示多边形。
* `convex_hull` 属性返回多边形的凸壳。
* `intersection()` 方法返回两个多边形的交集。

#### 3.2.2 点集最近点对查找

给定一个点集，可以通过计算点集的凸壳来查找点集中最近的点对。具体步骤如下：

1. 计算点集的凸壳。
2. 凸壳上的点按顺时针顺序排列。
3. 对于凸壳上的每个点，计算其与相邻两个点的距离。
4. 返回距离最小的点对。

**代码块：**

import math

def closest_pair(points):
    """查找点集中最近的点对。

    Args:
        points (list): 点集。

    Returns:
        tuple: 最近的点对。
    """

    # 计算点集的凸壳
    hull = convex_hull(points)

    # 凸壳上的点按顺时针顺序排列
    hull.sort(key=lambda point: math.atan2(point[1], point[0]))

    # 对于凸壳上的每个点，计算其与相邻两个点的距离
    min_dist = float('inf')
    closest_pair = None
    for i in range(len(hull)):
        j = (i + 1) % len(hull)
        k = (i + 2) % len(hull)
        dist = math.sqrt((hull[i][0] - hull[j][0])**2 + (hull[i][1] - hull[j][1])**2)
        if dist < min_dist:
            min_dist = dist
            closest_pair = (hull[i], hull[j])

    return closest_pair

**逻辑分析：**

* `convex_hull()` 函数计算点集的凸壳。
* 凸壳上的点按顺时针顺序排列。
* 循环遍历凸壳上的每个点，计算其与相邻两个点的距离。
* 返回距离最小的点对。

# 4. 凸包与凸壳的实战案例解析

### 4.1 凸包的实战案例

#### 4.1.1 计算多边形面积

**问题描述：**

给定一个多边形，求其面积。

**凸包应用：**

凸包可以用来计算多边形的面积。凸包是多边形的所有顶点的凸包络，它是一个凸多边形。凸多边形的面积可以通过以下公式计算：

def polygon_area(points):
    """
    计算多边形的面积。

    参数：
        points: 多边形的顶点列表，按逆时针顺序排列。

    返回：
        多边形的面积。
    """
    n = len(points)
    area = 0.0

    for i in range(n):
        x1, y1 = points[i]
        x2, y2 = points[(i + 1) % n]
        area += (x1 * y2 - x2 * y1)

    return abs(area) / 2.0

**代码逻辑分析：**

* 首先计算多边形的顶点数 `n`。
* 初始化面积 `area` 为 0.0。
* 遍历多边形的顶点，计算相邻两条边的叉积，并累加到 `area` 中。
* 最后返回 `area` 的绝对值除以 2.0，得到多边形的面积。

#### 4.1.2 计算多边形周长

**问题描述：**

给定一个多边形，求其周长。

**凸包应用：**

凸包可以用来计算多边形的周长。凸包的周长等于其所有边的长度之和。

def polygon_perimeter(points):
    """
    计算多边形的周长。

    参数：
        points: 多边形的顶点列表，按逆时针顺序排列。

    返回：
        多边形的周长。
    """
    n = len(points)
    perimeter = 0.0

    for i in range(n):
        x1, y1 = points[i]
        x2, y2 = points[(i + 1) % n]
        perimeter += math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)

    return perimeter

**代码逻辑分析：**

* 首先计算多边形的顶点数 `n`。
* 初始化周长 `perimeter` 为 0.0。
* 遍历多边形的顶点，计算相邻两条边的长度，并累加到 `perimeter` 中。
* 最后返回 `perimeter`，得到多边形的周长。

### 4.2 凸壳的实战案例

#### 4.2.1 多边形裁剪

**问题描述：**

给定一个多边形和一个裁剪窗口，裁剪多边形，只保留在裁剪窗口内的部分。

**凸壳应用：**

凸壳可以用来裁剪多边形。凸壳是多边形的所有顶点的凸包络，它是一个凸多边形。裁剪多边形时，只需要裁剪凸壳的部分即可。

def clip_polygon(polygon, window):
    """
    裁剪多边形。

    参数：
        polygon: 多边形的顶点列表，按逆时针顺序排列。
        window: 裁剪窗口的顶点列表，按逆时针顺序排列。

    返回：
        裁剪后的多边形的顶点列表。
    """
    # 计算多边形的凸壳
    convex_hull = convex_hull(polygon)

    # 计算裁剪窗口的凸壳
    window_hull = convex_hull(window)

    # 计算凸壳的交集
    intersection = convex_hull_intersection(convex_hull, window_hull)

    # 返回交集的顶点列表
    return intersection

**代码逻辑分析：**

* 首先计算多边形和裁剪窗口的凸壳。
* 然后计算凸壳的交集。
* 最后返回交集的顶点列表，即裁剪后的多边形的顶点列表。

#### 4.2.2 点集最近点对查找

**问题描述：**

给定一个点集，查找最近的点对。

**凸壳应用：**

凸壳可以用来查找点集中的最近点对。凸壳上的点一定是点集中最远的点，因此，凸壳上的点对一定是最远的点对。

def closest_pair(points):
    """
    查找点集中的最近点对。

    参数：
        points: 点集。

    返回：
        最近点对。
    """
    # 计算点集的凸壳
    convex_hull = convex_hull(points)

    # 查找凸壳上的最近点对
    closest_pair = None
    min_distance = float('inf')

    for i in range(len(convex_hull)):
        for j in range(i + 1, len(convex_hull)):
            distance = math.sqrt((convex_hull[i][0] - convex_hull[j][0]) ** 2 + (convex_hull[i][1] - convex_hull[j][1]) ** 2)
            if distance < min_distance:
                min_distance = distance
                closest_pair = (convex_hull[i], convex_hull[j])

    return closest_pair

**代码逻辑分析：**

* 首先计算点集的凸壳。
* 然后遍历凸壳上的所有点对，计算点对之间的距离。
* 最后返回距离最小的点对。

# 5. 凸包与凸壳的高级话题

### 5.1 凸包的拓展

#### 5.1.1 三维凸包

**概念：**

三维凸包是指三维空间中的一组点，其中任何两点之间的连线段都包含在凸包内。

**算法：**

计算三维凸包的算法与二维凸包类似，但复杂度更高。常用的算法包括：

- **快速凸包算法：**与二维凸包中的快速凸包算法类似，但需要对三维空间进行三角剖分。
- **分治算法：**将点集递归地分成较小的子集，并分别计算子集的凸包，然后合并这些凸包得到整个点集的凸包。

#### 5.1.2 动态凸包

**概念：**

动态凸包是指随着点集的动态变化而不断更新的凸包。

**算法：**

维护动态凸包的算法需要考虑点集的增删改。常用的算法包括：

- **增量算法：**当新点加入点集时，逐步更新凸包，保证凸包的性质。
- **减量算法：**当点从点集中删除时，逐步更新凸包，保证凸包的性质。

### 5.2 凸壳的拓展

#### 5.2.1 半平面交

**概念：**

半平面交是指求解一组半平面相交部分的算法。

**算法：**

常用的半平面交算法包括：

- **扫描线算法：**沿垂直于半平面法向量的扫描线进行扫描，维护当前扫描线上的半平面交。
- **分治算法：**将半平面集递归地分成较小的子集，并分别计算子集的半平面交，然后合并这些半平面交得到整个半平面集的半平面交。

#### 5.2.2 沃罗诺伊图

**概念：**

沃罗诺伊图是一种将平面或空间划分为多个区域的结构，每个区域包含到该区域内某一点最近的所有点。

**算法：**

计算沃罗诺伊图的算法包括：

- **增量算法：**逐步添加点到点集中，并更新沃罗诺伊图。
- **分治算法：**将点集递归地分成较小的子集，并分别计算子集的沃罗诺伊图，然后合并这些沃罗诺伊图得到整个点集的沃罗诺伊图。

# 6. 凸包与凸壳的总结与展望

**6.1 凸包与凸壳的总结**

凸包和凸壳是计算几何中两个重要的概念，它们在许多领域都有着广泛的应用。通过本章的学习，我们对凸包和凸壳的算法、性质和应用有了深入的理解。

**6.2 凸包与凸壳的展望**

随着计算几何的发展，凸包和凸壳的研究也在不断深入。目前，凸包和凸壳的研究主要集中在以下几个方面：

* **算法的优化：**不断探索更有效率的凸包和凸壳算法，以应对大规模数据集的处理。
* **拓展应用：**将凸包和凸壳应用到更多的领域，例如计算机图形学、机器人学和数据分析等。
* **理论研究：**深入研究凸包和凸壳的理论性质，探索新的算法和优化技术。

**6.3 凸包与凸壳的未来发展**

凸包和凸壳在计算几何领域具有重要的地位，随着技术的不断发展，它们在未来将发挥越来越重要的作用。我们可以期待在以下几个方面取得突破：

* **实时处理：**开发能够实时处理大规模凸包和凸壳的算法，满足实时应用的需求。
* **分布式计算：**探索分布式计算技术，将凸包和凸壳算法应用到分布式系统中，提高计算效率。
* **人工智能：**将人工智能技术与凸包和凸壳相结合，开发新的算法和优化技术，增强凸包和凸壳的处理能力。

总之，凸包和凸壳的研究和应用前景广阔，相信在未来将取得更多的突破，为计算几何领域的发展做出更大贡献。