一文读懂笛卡尔坐标系中的直线方程：公式、性质、应用

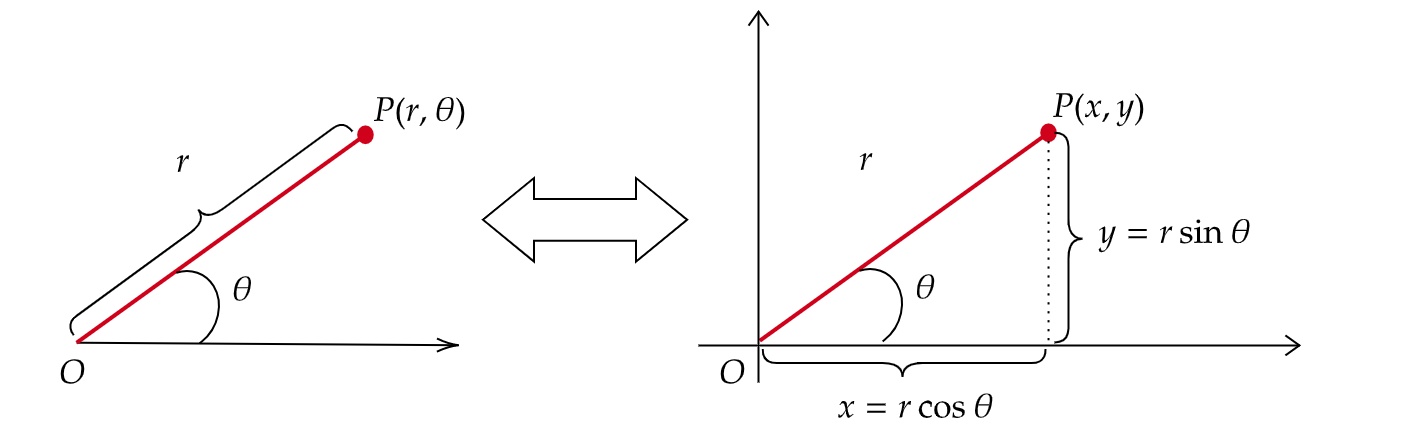
# 1. 笛卡尔坐标系中的直线基本概念

在笛卡尔坐标系中，一条直线可以由其斜率和截距来唯一确定。

**斜率**表示直线与水平轴所成的夹角的正切值。斜率为正时，直线从左向右上升；斜率为负时，直线从左向右下降；斜率为零时，直线平行于水平轴。

**截距**表示直线与垂直轴的交点。截距为正时，直线在垂直轴上方；截距为负时，直线在垂直轴下方；截距为零时，直线经过原点。

# 2. 直线方程的求解

直线方程是描述直线的一种数学表达式，它可以用来确定直线的位置、斜率和截距。在笛卡尔坐标系中，直线方程通常有四种基本形式：点斜式、两点式、斜截式和截距式。

### 2.1 点斜式方程

点斜式方程的表达式为：

y - y1 = m(x - x1)

其中，`(x1, y1)` 是直线上已知的一点，`m` 是直线的斜率。

**参数说明：**

* `(x1, y1)`：直线上已知点的坐标
* `m`：直线的斜率

**代码示例：**

import matplotlib.pyplot as plt

# 已知点 (1, 2) 和斜率 m = 2
x1 = 1
y1 = 2
m = 2

# 点斜式方程
y = y1 + m * (x - x1)

# 绘制直线
plt.plot([0, 5], [y(0), y(5)], color='blue')
plt.show()

**逻辑分析：**

代码首先定义了直线上已知点的坐标和斜率。然后，它使用点斜式方程计算了直线上其他点的坐标。最后，它使用 matplotlib 绘制了直线。

### 2.2 两点式方程

两点式方程的表达式为：

(y - y1)(x2 - x1) = (y2 - y1)(x - x1)

其中，`(x1, y1)` 和 `(x2, y2)` 是直线上已知的两点。

**参数说明：**

* `(x1, y1)` 和 `(x2, y2)`：直线上已知的两点坐标

**代码示例：**

import matplotlib.pyplot as plt

# 已知两点 (1, 2) 和 (3, 6)
x1 = 1
y1 = 2
x2 = 3
y2 = 6

# 两点式方程
y = ((y2 - y1) / (x2 - x1)) * (x - x1) + y1

# 绘制直线
plt.plot([0, 5], [y(0), y(5)], color='red')
plt.show()

**逻辑分析：**

代码首先定义了直线上已知的两点坐标。然后，它使用两点式方程计算了直线上其他点的坐标。最后，它使用 matplotlib 绘制了直线。

### 2.3 斜截式方程

斜截式方程的表达式为：

y = mx + b

其中，`m` 是直线的斜率，`b` 是直线的截距。

**参数说明：**

* `m`：直线的斜率
* `b`：直线的截距

**代码示例：**

import matplotlib.pyplot as plt

# 斜率 m = 2，截距 b = 1
m = 2
b = 1

# 斜截式方程
y = m * x + b

# 绘制直线
plt.plot([0, 5], [y(0), y(5)], color='green')
plt.show()

**逻辑分析：**

代码首先定义了直线的斜率和截距。然后，它使用斜截式方程计算了直线上其他点的坐标。最后，它使用 matplotlib 绘制了直线。

### 2.4 截距式方程

截距式方程的表达式为：

x = a

或

y = b

其中，`a` 是直线的 x 截距，`b` 是直线的 y 截距。

**参数说明：**

* `a`：直线的 x 截距
* `b`：直线的 y 截距

**代码示例：**

import matplotlib.pyplot as plt

# x 截距 a = 2
a = 2

# 截距式方程
x = a

# 绘制直线
plt.plot([a, a], [0, 5], color='black')
plt.show()

**逻辑分析：**

代码首先定义了直线的 x 截距。然后，它使用截距式方程计算了直线上其他点的坐标。最后，它使用 matplotlib 绘制了直线。

# 3.1 直线的斜率与截距

**斜率**

直线斜率表示直线与 x 轴所成的角的正切值，反映了直线在 y 轴方向上的变化率。斜率记作 k，其计算公式为：

k = (y2 - y1) / (x2 - x1)

其中，(x1, y1) 和 (x2, y2) 是直线上任意两点。

**截距**

直线截距表示直线与 y 轴的交点纵坐标，反映了直线在 y 轴方向上的位置。截距记作 b，其计算公式为：

b = y - kx

其中，(x, y) 是直线上任意一点，k 是直线斜率。

**斜率与截距的几何意义**

* 斜率 k 表示直线每向右移动一个单位，向上的变化量。
* 截距 b 表示直线与 y 轴的交点，即当 x = 0 时的 y 值。

**斜率与截距的应用**

斜率和截距在直线方程的求解、直线性质的判断以及直线方程的应用中都有着重要的作用。例如，通过斜率和截距可以判断直线是平行、垂直还是相交，还可以求出直线与其他图形的交点。

### 3.2 直线的平行与垂直

**平行直线**

两条直线平行当且仅当它们的斜率相等。即：

k1 = k2

其中，k1 和 k2 分别是两条直线的斜率。

**垂直直线**

两条直线垂直当且仅当它们的斜率互为负倒数。即：

k1 * k2 = -1

其中，k1 和 k2 分别是两条直线的斜率。

**判断直线平行或垂直的步骤**

1. 求出两条直线的斜率 k1 和 k2。
2. 根据上述条件判断两条直线是否平行或垂直。

### 3.3 直线的交点与夹角

**交点**

两条直线的交点是它们同时满足的坐标点。求解两条直线的交点可以采用以下步骤：

1. 将两条直线方程化为斜截式：

   y = k1x + b1
   y = k2x + b2

2. 令两条直线方程相等：

   k1x + b1 = k2x + b2

3. 解出 x：

   x = (b2 - b1) / (k1 - k2)

4. 将求出的 x 值代入任意一条直线方程，求出 y：

   y = k1x + b1

**夹角**

两条直线的夹角是它们所成角的度数。求解两条直线的夹角可以采用以下公式：

θ = arctan(|(k2 - k1) / (1 + k1 * k2)|)

其中，k1 和 k2 分别是两条直线的斜率，θ 是两条直线的夹角。

# 4. 直线方程的应用

### 4.1 直线与圆的交点

#### 4.1.1 问题描述

求直线与圆的交点坐标。

#### 4.1.2 解法

**步骤 1：** 将直线方程化简为斜截式方程：`y = mx + b`

**步骤 2：** 将直线方程代入圆方程：`x^2 + y^2 = r^2`

**步骤 3：** 解得二次方程：`x^2 + (mx + b)^2 = r^2`

**步骤 4：** 根据判别式求出交点个数：

* 若判别式大于 0，则有 2 个交点。
* 若判别式等于 0，则有 1 个交点（切点）。
* 若判别式小于 0，则没有交点。

**步骤 5：** 求出交点坐标：

* 将求得的 x 值代入直线方程，求出 y 值。
* 将求得的 y 值代入圆方程，求出 x 值。

#### 4.1.3 代码示例

import sympy

# 定义直线方程
m = sympy.Symbol("m")
b = sympy.Symbol("b")
line_eq = sympy.Eq(sympy.Symbol("y"), m * sympy.Symbol("x") + b)

# 定义圆方程
r = sympy.Symbol("r")
circle_eq = sympy.Eq(sympy.Symbol("x")**2 + sympy.Symbol("y")**2, r**2)

# 求解交点
result = sympy.solve([line_eq, circle_eq], (sympy.Symbol("x"), sympy.Symbol("y")))

# 输出交点坐标
print("交点坐标：", result)

**代码逻辑分析：**

* 使用 `sympy` 库定义直线和圆的方程。
* 使用 `sympy.solve()` 函数求解方程组，得到交点坐标。
* 输出交点坐标。

### 4.2 直线与抛物的交点

#### 4.2.1 问题描述

求直线与抛物的交点坐标。

#### 4.2.2 解法

**步骤 1：** 将直线方程化简为斜截式方程：`y = mx + b`

**步骤 2：** 将直线方程代入抛物线方程：`y = ax^2 + bx + c`

**步骤 3：** 解得二次方程：`ax^2 + (b + m)x + (c - b) = 0`

**步骤 4：** 根据判别式求出交点个数：

* 若判别式大于 0，则有 2 个交点。
* 若判别式等于 0，则有 1 个交点（切点）。
* 若判别式小于 0，则没有交点。

**步骤 5：** 求出交点坐标：

* 将求得的 x 值代入直线方程，求出 y 值。
* 将求得的 y 值代入抛物线方程，求出 x 值。

#### 4.2.3 代码示例

import sympy

# 定义直线方程
m = sympy.Symbol("m")
b = sympy.Symbol("b")
line_eq = sympy.Eq(sympy.Symbol("y"), m * sympy.Symbol("x") + b)

# 定义抛物线方程
a = sympy.Symbol("a")
b = sympy.Symbol("b")
c = sympy.Symbol("c")
parabola_eq = sympy.Eq(sympy.Symbol("y"), a * sympy.Symbol("x")**2 + b * sympy.Symbol("x") + c)

# 求解交点
result = sympy.solve([line_eq, parabola_eq], (sympy.Symbol("x"), sympy.Symbol("y")))

# 输出交点坐标
print("交点坐标：", result)

**代码逻辑分析：**

* 使用 `sympy` 库定义直线和抛物线的方程。
* 使用 `sympy.solve()` 函数求解方程组，得到交点坐标。
* 输出交点坐标。

### 4.3 直线与椭圆的交点

#### 4.3.1 问题描述

求直线与椭圆的交点坐标。

#### 4.3.2 解法

**步骤 1：** 将直线方程化简为斜截式方程：`y = mx + b`

**步骤 2：** 将直线方程代入椭圆方程：`(x^2 / a^2) + (y^2 / b^2) = 1`

**步骤 3：** 解得二次方程：`(x^2 / a^2) + ((mx + b)^2 / b^2) = 1`

**步骤 4：** 根据判别式求出交点个数：

* 若判别式大于 0，则有 2 个交点。
* 若判别式等于 0，则有 1 个交点（切点）。
* 若判别式小于 0，则没有交点。

**步骤 5：** 求出交点坐标：

* 将求得的 x 值代入直线方程，求出 y 值。
* 将求得的 y 值代入椭圆方程，求出 x 值。

#### 4.3.3 代码示例

import sympy

# 定义直线方程
m = sympy.Symbol("m")
b = sympy.Symbol("b")
line_eq = sympy.Eq(sympy.Symbol("y"), m * sympy.Symbol("x") + b)

# 定义椭圆方程
a = sympy.Symbol("a")
b = sympy.Symbol("b")
ellipse_eq = sympy.Eq((sympy.Symbol("x")**2 / a**2) + (sympy.Symbol("y")**2 / b**2), 1)

# 求解交点
result = sympy.solve([line_eq, ellipse_eq], (sympy.Symbol("x"), sympy.Symbol("y")))

# 输出交点坐标
print("交点坐标：", result)

**代码逻辑分析：**

* 使用 `sympy` 库定义直线和椭圆的方程。
* 使用 `sympy.solve()` 函数求解方程组，得到交点坐标。
* 输出交点坐标。

# 5. 直线方程的拓展

### 5.1 参数方程

**定义：**

参数方程是一种用参数表示直线方程的方式，其中参数通常用 t 表示。直线上的任意一点都可以用参数 t 的值来表示。

**形式：**

x = x0 + at
y = y0 + bt

其中，(x0, y0) 是直线上一点的坐标，a 和 b 是直线的斜率和截距。

**参数方程与其他直线方程之间的关系：**

* 点斜式方程：当 t = 0 时，x = x0，y = y0，因此点斜式方程可以看作是参数方程在 t = 0 时的特殊情况。
* 斜截式方程：当 t = 1 时，x = x0 + a，y = y0 + b，因此斜截式方程可以看作是参数方程在 t = 1 时的特殊情况。

**代码示例：**

import matplotlib.pyplot as plt

# 定义直线参数方程
x0 = 1
y0 = 2
a = 3
b = 4

# 创建参数值范围
t = np.linspace(0, 10, 100)

# 计算直线上点的坐标
x = x0 + a * t
y = y0 + b * t

# 绘制直线
plt.plot(x, y)
plt.show()

**逻辑分析：**

* `matplotlib.pyplot` 模块用于绘制图形。
* `np.linspace` 函数创建了一个参数值范围，从 0 到 10，间隔为 0.1。
* 使用参数方程计算直线上点的坐标。
* `plt.plot` 函数绘制直线。

### 5.2 向量方程

**定义：**

向量方程是一种用向量表示直线方程的方式。直线上的任意一点都可以用一个向量表示，该向量从直线上的一个固定点指向该点。

**形式：**

r = r0 + tv

其中，r0 是直线上一点的坐标向量，v 是直线的方向向量，t 是参数。

**向量方程与其他直线方程之间的关系：**

* 点斜式方程：向量方程中 r0 是直线上一点的坐标，v 是直线的斜率向量。
* 斜截式方程：向量方程中 r0 是直线的截距点，v 是直线的斜率向量。

**代码示例：**

import numpy as np

# 定义直线向量方程
r0 = np.array([1, 2])
v = np.array([3, 4])

# 创建参数值范围
t = np.linspace(0, 10, 100)

# 计算直线上点的坐标
r = r0 + t * v

# 输出直线上点的坐标
print(r)

**逻辑分析：**

* `numpy` 模块用于处理向量和矩阵。
* 创建直线向量方程中使用的向量。
* 使用参数方程计算直线上点的坐标。
* 输出直线上点的坐标。

### 5.3 一般式方程

**定义：**

一般式方程是一种用 Ax + By + C = 0 的形式表示直线方程的方式。

**形式：**

Ax + By + C = 0

其中，A、B 和 C 是常数。

**一般式方程与其他直线方程之间的关系：**

* 点斜式方程：可以将点斜式方程化为一般式方程，方法是将方程两边同时乘以 B。
* 斜截式方程：可以将斜截式方程化为一般式方程，方法是将方程两边同时乘以 A。

**代码示例：**

# 定义直线一般式方程
A = 3
B = 4
C = 5

# 计算直线上一点的坐标
x = -C / A
y = -C / B

# 输出直线上一点的坐标
print(x, y)

**逻辑分析：**

* 创建直线一般式方程中使用的常数。
* 使用一般式方程计算直线上一点的坐标。
* 输出直线上一点的坐标。

# 6. 直线方程在实际中的应用

直线方程在实际生活中有着广泛的应用，从物理学到经济学再到工程学，它都能发挥重要的作用。

### 6.1 物理学中的运动直线

在物理学中，直线方程可以用来描述物体的运动轨迹。例如，一个以恒定速度运动的物体，其运动轨迹是一条直线。直线方程可以用来计算物体的位置、速度和加速度。

# 物体运动直线方程
position = initial_position + velocity * time

### 6.2 经济学中的供求曲线

在经济学中，直线方程可以用来表示供求曲线。供求曲线描述了商品或服务在不同价格水平下的供给量和需求量。通过分析供求曲线，经济学家可以预测市场价格和产量。

# 供求曲线方程
supply = a + b * price
demand = c + d * price

### 6.3 工程学中的设计图纸

在工程学中，直线方程可以用来表示设计图纸中的直线。直线方程可以用来计算直线的长度、斜率和截距。这些信息对于设计和制造产品至关重要。

# 设计图纸直线方程
y = mx + b