笛卡尔坐标系与极坐标系转换：公式、性质、应用

# 1. 笛卡尔坐标系与极坐标系的定义和基本概念

### 1.1 笛卡尔坐标系

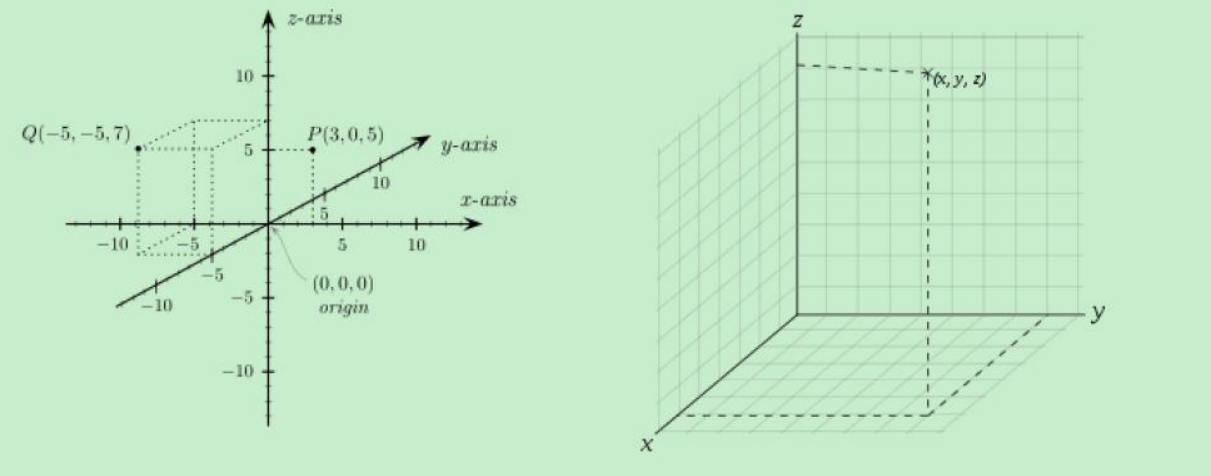
笛卡尔坐标系是一种二维坐标系，由两条相互垂直的直线轴组成，称为 x 轴和 y 轴。每个点由其在 x 轴和 y 轴上的投影距离表示，称为 x 坐标和 y 坐标。

### 1.2 极坐标系

极坐标系是一种二维坐标系，由一个原点和一条从原点射出的射线（极轴）组成。每个点由其到原点的距离（极径）和它与极轴之间的夹角（极角）表示。

# 2. 笛卡尔坐标系与极坐标系之间的转换公式

笛卡尔坐标系和极坐标系是两种不同的坐标系，它们在不同的应用场景中具有各自的优势。笛卡尔坐标系使用一对直角轴来表示点的位置，而极坐标系使用一个原点、一个角度和一个距离来表示点的位置。在某些情况下，需要在笛卡尔坐标系和极坐标系之间进行转换。

### 2.1 从笛卡尔坐标系到极坐标系的转换

从笛卡尔坐标系到极坐标系的转换公式如下：

r = √(x² + y²)
θ = arctan(y / x)

其中：

* `r` 是极坐标系中的距离
* `θ` 是极坐标系中的角度
* `x` 是笛卡尔坐标系中的横坐标
* `y` 是笛卡尔坐标系中的纵坐标

**代码块：**

import math

def cartesian_to_polar(x, y):
    """
    从笛卡尔坐标系转换到极坐标系。

    参数：
        x: 笛卡尔坐标系中的横坐标
        y: 笛卡尔坐标系中的纵坐标

    返回：
        极坐标系中的距离和角度元组
    """

    r = math.sqrt(x**2 + y**2)
    theta = math.atan2(y, x)
    return r, theta

**代码逻辑分析：**

* `math.sqrt(x**2 + y**2)` 计算笛卡尔坐标系中点到原点的距离。
* `math.atan2(y, x)` 计算笛卡尔坐标系中点与 x 轴之间的角度。

### 2.2 从极坐标系到笛卡尔坐标系的转换

从极坐标系到笛卡尔坐标系的转换公式如下：

x = r * cos(θ)
y = r * sin(θ)

其中：

* `x` 是笛卡尔坐标系中的横坐标
* `y` 是笛卡尔坐标系中的纵坐标
* `r` 是极坐标系中的距离
* `θ` 是极坐标系中的角度

**代码块：**

import math

def polar_to_cartesian(r, theta):
    """
    从极坐标系转换到笛卡尔坐标系。

    参数：