揭秘笛卡尔坐标系：掌握距离、角度计算的终极指南

# 1. 笛卡尔坐标系的理论基础**

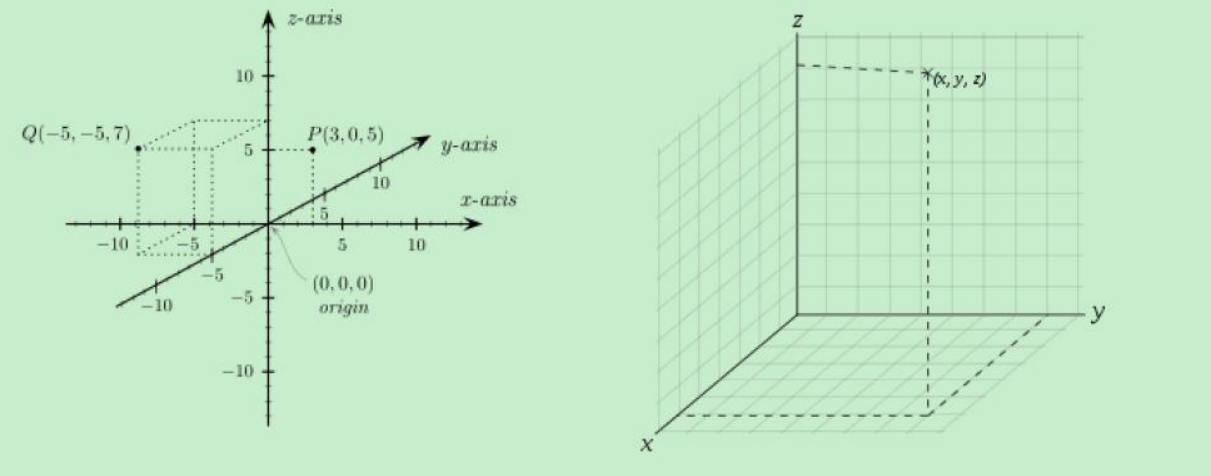
笛卡尔坐标系，也称为直角坐标系，是一种二维或三维空间中的几何系统，用于表示点的位置和描述几何形状。它由两条或三条相互垂直的直线（称为坐标轴）组成，形成一个平面或空间。

笛卡尔坐标系的原点是坐标轴相交的点，每个坐标轴上都有一个单位长度的刻度。点的坐标是其相对于坐标轴的距离，通常表示为有序对或有序三元组。例如，在二维笛卡尔坐标系中，点 (3, 4) 表示从原点向右移动 3 个单位，然后向上移动 4 个单位。

# 2. 笛卡尔坐标系中的距离计算

笛卡尔坐标系是描述和计算空间中点、线和面的位置和关系的数学工具。在笛卡尔坐标系中，距离计算是基本且重要的操作之一。本章将深入探讨笛卡尔坐标系中距离计算的各种公式和方法。

### 2.1 平面内两点之间的距离公式

在平面内，两点之间的距离可以由欧几里得距离公式计算，该公式为：

d = √((x2 - x1)² + (y2 - y1)²)

其中：

- `d` 是两点之间的距离
- `(x1, y1)` 是第一点的坐标
- `(x2, y2)` 是第二点的坐标

**代码块：**

import math

def distance_between_two_points(x1, y1, x2, y2):
  """计算平面内两点之间的距离。

  Args:
    x1: 第一点的 x 坐标。
    y1: 第一点的 y 坐标。
    x2: 第二点的 x 坐标。
    y2: 第二点的 y 坐标。

  Returns:
    两点之间的距离。
  """

  dx = x2 - x1
  dy = y2 - y1
  distance = math.sqrt(dx**2 + dy**2)
  return distance

**逻辑分析：**

该代码块实现了平面内两点之间距离的计算。它首先计算两点之间的 x 坐标和 y 坐标的差值，然后使用勾股定理计算两点之间的距离。

### 2.2 空间内两点之间的距离公式

在三维空间中，两点之间的距离可以由欧几里得距离公式的扩展版本计算，该公式为：

d = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)

其中：

- `d` 是两点之间的距离
- `(x1, y1, z1)` 是第一点的坐标
- `(x2, y2, z2)` 是第二点的坐标

**代码块：**

import math

def distance_between_two_points_in_3d(x1, y1, z1, x2, y2, z2):
  """计算空间内两点之间的距离。

  Args:
    x1: 第一点的 x 坐标。
    y1: 第一点的 y 坐标。
    z1: 第一点的 z 坐标。
    x2: 第二点的 x 坐标。
    y2: 第二点的 y 坐标。
    z2: 第二点的 z 坐标。

  Returns:
    两点之间的距离。
  """

  dx = x2 - x1
  dy = y2 - y1
  dz = z2 - z1
  distance = math.sqrt(dx**2 + dy**2 + dz**2)
  return distance

**逻辑分析：**

该代码块实现了空间内两点之间距离的计算。它首先计算两点之间的 x 坐标、y 坐标和 z 坐标的差值，然后使用勾股定理计算两点之间的距离。

### 2.3 点到直线的距离公式

在笛卡尔坐标系中，点到直线的距离可以由以下公式计算：

d = |Ax + By + C| / √(A² + B²)

其中：

- `d` 是点到直线的距离
- `(x, y)` 是点的坐标
- `Ax + By + C = 0` 是直线的方程

**代码块：**

import math

def distance_from_point_to_line(x, y, A, B, C):
  """计算点到直线的距离。

  Args:
    x: 点的 x 坐标。
    y: 点的 y 坐标。
    A: 直线方程中的 A 系数。
    B: 直线方程中的 B 系数。
    C: 直线方程中的 C 系数。

  Returns:
    点到直线的距离。
  """

  distance = abs(A * x + B * y + C) / math.sqrt(A**2 + B**2)
  return distance

**逻辑分析：**

该代码块实现了点到直线的距离的计算。它首先计算点到直线的垂线方程，然后使用绝对值函数计算垂线与直线的距离。

### 2.4 点到平面的距离公式

在笛卡尔坐标系中，点到平面的距离可以由以下公式计算：

d = |Ax + By + Cz + D| / √(A² + B² + C²)

其中：

- `d` 是点到平面的距离
- `(x, y, z)` 是点的坐标
- `Ax + By + Cz + D = 0` 是平面的方程

**代码块：**

import math

def distance_from_point_to_plane(x, y, z, A, B, C, D):
  """计算点到平面的距离。

  Args:
    x: 点的 x 坐标。
    y: 点的 y 坐标。
    z: 点的 z 坐标。
    A: 平面方程中的 A 系数。
    B: 平面方程中的 B 系数。
    C: 平面方程中的 C 系数。
    D: 平面方程中的 D 系数。

  Returns:
    点到平面的距离。
  """

  distance = abs(A * x + B * y + C * z + D) / math.sqrt(A**2 + B**2 + C**2)
  return distance

**逻辑分析：**

该代码块实现了点到平面的距离的计算。它首先计算点到平面的垂线方程，然后使用绝对值函数计算垂线与平面的距离。

# 3. 笛卡尔坐标系中的角度计算

笛卡尔坐标系不仅可以用来计算距离，还可以用来计算角度。本章节将介绍笛卡尔坐标系中计算两条直线、直线与平面、平面与平面之间夹角的公式和方法。

### 3.1 两条直线之间的夹角公式

两条直线之间的夹角是指两条直线相交或平行时，它们所形成的角。在笛卡尔坐标系中，两条直线之间的夹角可以用以下公式计算：

cosθ = (x1 * x2 + y1 * y2) / (√(x1^2 + y1^2) * √(x2^2 + y2^2))

其中：

* `θ` 是两条直线之间的夹角
* `(x1, y1)` 和 `(x2, y2)` 是两条直线的斜率

**代码块：**

import math

def angle_between_lines(x1, y1, x2, y2):
  """
  计算两条直线之间的夹角。

  参数：
    x1, y1: 第一條直线的斜率
    x2, y2: 第二條直线的斜率

  返回：
    两条直线之间的夹角（弧度）
  """

  numerator = x1 * x2 + y1 * y2
  denominator = math.sqrt(x1**2 + y1**2) * math.sqrt(x2**2 + y2**2)
  cos_theta = numerator / denominator
  theta = math.acos(cos_theta)
  return theta

**逻辑分析：**

该代码块实现了计算两条直线之间夹角的函数。函数接收两条直线的斜率作为参数，并返回两条直线之间的夹角（弧度）。

函数首先计算两条直线的斜率的点积，然后计算两条直线的斜率的模长的乘积。然后，函数计算两条直线的斜率的点积与两条直线的斜率的模长的乘积的商，得到两条直线之间的夹角的余弦值。最后，函数使用 `math.acos()` 函数将余弦值转换为弧度值。

### 3.2 直线与平面之间的夹角公式

直线与平面之间的夹角是指直线与平面相交时，直线与平面法线向量之间的夹角。在笛卡尔坐标系中，直线与平面之间的夹角可以用以下公式计算：

cosθ = |(x1 * a + y1 * b + z1 * c + d) / √(a^2 + b^2 + c^2)|

其中：

* `θ` 是直线与平面之间的夹角
* `(x1, y1, z1)` 是直线上的任意一点
* `(a, b, c)` 是平面的法线向量
* `d` 是平面的截距

**代码块：**

import math

def angle_between_line_and_plane(x1, y1, z1, a, b, c, d):
  """
  计算直线与平面之间的夹角。

  参数：
    x1, y1, z1: 直线上的任意一点
    a, b, c: 平面的法线向量
    d: 平面的截距

  返回：
    直线与平面之间的夹角（弧度）
  """

  numerator = abs(x1 * a + y1 * b + z1 * c + d)
  denominator = math.sqrt(a**2 + b**2 + c**2)
  cos_theta = numerator / denominator
  theta = math.acos(cos_theta)
  return theta

**逻辑分析：**

该代码块实现了计算直线与平面之间夹角的函数。函数接收直线上的任意一点和平面的法线向量和截距作为参数，并返回直线与平面之间的夹角（弧度）。

函数首先计算直线上的任意一点与平面的法线向量的点积，然后计算平面的法线向量的模长。然后，函数计算直线上的任意一点与平面的法线向量的点积与平面的法线向量的模长的商，得到直线与平面之间的夹角的余弦值。最后，函数使用 `math.acos()` 函数将余弦值转换为弧度值。

### 3.3 平面与平面之间的夹角公式

平面与平面之间的夹角是指两个平面相交时，两个平面法线向量之间的夹角。在笛卡尔坐标系中，平面与平面之间的夹角可以用以下公式计算：

cosθ = |(a1 * a2 + b1 * b2 + c1 * c2) / (√(a1^2 + b1^2 + c1^2) * √(a2^2 + b2^2 + c2^2))|

其中：

* `θ` 是平面与平面之间的夹角
* `(a1, b1, c1)` 和 `(a2, b2, c2)` 是两个平面的法线向量

**代码块：**

import math

def angle_between_planes(a1, b1, c1, a2, b2, c2):
  """
  计算平面与平面之间的夹角。

  参数：
    a1, b1, c1: 第一个平面的法线向量
    a2, b2, c2: 第二个平面的法线向量

  返回：
    平面与平面之间的夹角（弧度）
  """

  numerator = abs(a1 * a2 + b1 * b2 + c1 * c2)
  denominator = math.sqrt(a1**2 + b1**2 + c1**2) * math.sqrt(a2**2 + b2**2 + c2**2)
  cos_theta = numerator / denominator
  theta = math.acos(cos_theta)
  return theta

**逻辑分析：**

该代码块实现了计算平面与平面之间夹角的函数。函数接收两个平面的法线向量作为参数，并返回平面与平面之间的夹角（弧度）。

函数首先计算两个平面的法线向量的点积，然后计算两个平面的法线向量的模长的乘积。然后，函数计算两个平面的法线向量的点积与两个平面的法线向量的模长的乘积的商，得到平面与平面之间的夹角的余弦值。最后，函数使用 `math.acos()` 函数将余弦值转换为弧度值。

# 4. 笛卡尔坐标系在实践中的应用**

笛卡尔坐标系不仅在理论上具有重要的意义，在实际应用中也发挥着至关重要的作用。本章节将探讨笛卡尔坐标系在物理学、工程学和计算机图形学等领域的应用。

**4.1 物理学中的应用：运动学和力学**

笛卡尔坐标系在物理学中有着广泛的应用，特别是运动学和力学领域。在运动学中，笛卡尔坐标系用于描述物体的运动，例如位置、速度和加速度。通过使用笛卡尔坐标系，我们可以计算物体运动的轨迹和速度。

import numpy as np

# 定义一个函数来计算物体的运动轨迹
def calculate_trajectory(initial_position, initial_velocity, acceleration, time):
    """
    计算物体的运动轨迹。

    参数：
        initial_position：物体的初始位置（笛卡尔坐标系中的三维向量）
        initial_velocity：物体的初始速度（笛卡尔坐标系中的三维向量）
        acceleration：物体的加速度（笛卡尔坐标系中的三维向量）
        time：时间（标量）

    返回：
        物体的运动轨迹（笛卡尔坐标系中的三维向量列表）
    """

    # 计算物体的速度
    velocity = initial_velocity + acceleration * time

    # 计算物体的位移
    displacement = velocity * time

    # 计算物体的运动轨迹
    trajectory = initial_position + displacement

    return trajectory

在力学中，笛卡尔坐标系用于描述力，例如力的大小和方向。通过使用笛卡尔坐标系，我们可以计算物体的受力情况和运动状态。

import numpy as np

# 定义一个函数来计算物体的受力情况
def calculate_forces(mass, acceleration):
    """
    计算物体的受力情况。

    参数：
        mass：物体的质量（标量）
        acceleration：物体的加速度（笛卡尔坐标系中的三维向量）

    返回：
        物体的受力（笛卡尔坐标系中的三维向量）
    """

    # 计算物体的受力
    force = mass * acceleration

    return force

**4.2 工程学中的应用：几何设计和结构分析**

笛卡尔坐标系在工程学中也有着广泛的应用，特别是几何设计和结构分析领域。在几何设计中，笛卡尔坐标系用于描述物体的形状和尺寸。通过使用笛卡尔坐标系，我们可以创建物体的三维模型和进行几何分析。

import numpy as np

# 定义一个函数来创建物体的三维模型
def create_3d_model(vertices, faces):
    """
    创建物体的三维模型。

    参数：
        vertices：物体的顶点（笛卡尔坐标系中的三维向量列表）
        faces：物体的面（顶点索引的三元组列表）

    返回：
        物体的三维模型（网格对象）
    """

    # 创建网格对象
    mesh = trimesh.Trimesh(vertices, faces)

    return mesh

在结构分析中，笛卡尔坐标系用于描述结构的受力情况和变形。通过使用笛卡尔坐标系，我们可以计算结构的应力和应变，并进行结构安全分析。

import numpy as np

# 定义一个函数来计算结构的应力
def calculate_stress(forces, area):
    """
    计算结构的应力。

    参数：
        forces：作用在结构上的力（笛卡尔坐标系中的三维向量列表）
        area：结构的受力面积（标量）

    返回：
        结构的应力（笛卡尔坐标系中的三维向量）
    """

    # 计算结构的应力
    stress = forces / area

    return stress

**4.3 计算机图形学中的应用：三维建模和动画**

笛卡尔坐标系在计算机图形学中也有着重要的应用，特别是三维建模和动画领域。在三维建模中，笛卡尔坐标系用于描述物体的形状和位置。通过使用笛卡尔坐标系，我们可以创建物体的三维模型并进行渲染。

import numpy as np

# 定义一个函数来创建物体的三维模型
def create_3d_model(vertices, faces):
    """
    创建物体的三维模型。

    参数：
        vertices：物体的顶点（笛卡尔坐标系中的三维向量列表）
        faces：物体的面（顶点索引的三元组列表）

    返回：
        物体的三维模型（网格对象）
    """

    # 创建网格对象
    mesh = trimesh.Trimesh(vertices, faces)

    return mesh

在动画中，笛卡尔坐标系用于描述物体的运动。通过使用笛卡尔坐标系，我们可以创建物体的动画并进行渲染。

import numpy as np

# 定义一个函数来创建物体的动画
def create_animation(model, trajectory):
    """
    创建物体的动画。

    参数：
        model：物体的三维模型（网格对象）
        trajectory：物体的运动轨迹（笛卡尔坐标系中的三维向量列表）

    返回：
        物体的动画（视频文件）
    """

    # 创建动画
    animation = model.animation(trajectory)

    # 渲染动画
    animation.render()

    return animation

# 5. 笛卡尔坐标系的进阶技巧

笛卡尔坐标系是数学中一种强大的工具，但它并不局限于计算距离和角度。本章节将介绍笛卡尔坐标系的进阶技巧，包括参数方程、极坐标系、向量分析、线性代数、微积分和积分学。

### 5.1 参数方程和极坐标系

**参数方程**

参数方程是一种表示平面或空间中曲线的方程。它使用一个或多个参数来表示曲线上点的坐标。例如，以下参数方程表示一条圆：

x = r * cos(t)
y = r * sin(t)

其中，`r` 是圆的半径，`t` 是参数。

**极坐标系**

极坐标系是一种二维坐标系，使用极角和极径来表示平面上的点。极角是从正 x 轴逆时针旋转到该点的角度，极径是从原点到该点的距离。

x = r * cos(θ)
y = r * sin(θ)

其中，`r` 是极径，`θ` 是极角。

### 5.2 向量分析和线性代数

**向量分析**

向量分析是数学中一个分支，它研究向量和标量。向量是一个具有大小和方向的量，而标量是一个只有大小的量。向量分析在物理学和工程学中有着广泛的应用。

**线性代数**

线性代数是数学中一个分支，它研究向量空间和线性变换。向量空间是一个由向量组成的集合，线性变换是将一个向量空间映射到另一个向量空间的函数。线性代数在计算机图形学、机器学习和数据科学中有着广泛的应用。

### 5.3 微积分和积分学

**微积分**

微积分是数学中一个分支，它研究变化率和积分。微积分在物理学、工程学和经济学中有着广泛的应用。

**积分学**

积分学是微积分中一个分支，它研究函数的积分。积分可以用来计算面积、体积和长度。积分学在物理学、工程学和经济学中有着广泛的应用。

### 5.4 进阶技巧在实践中的应用

笛卡尔坐标系的进阶技巧在实践中有着广泛的应用，包括：

* **物理学：**参数方程用于描述运动的轨迹，向量分析用于描述力。
* **工程学：**线性代数用于解决结构分析问题，积分学用于计算体积和面积。
* **计算机图形学：**参数方程用于创建三维模型，向量分析用于计算光照和阴影。
* **机器学习：**线性代数用于解决分类和回归问题，积分学用于计算概率分布。

# 6. 笛卡尔坐标系在现实世界中的案例

### 6.1 GPS导航系统

笛卡尔坐标系在GPS导航系统中发挥着至关重要的作用。GPS接收器通过接收来自多颗卫星的信号，可以确定其在地球上的三维位置。

import math

# 接收器坐标
receiver_x = 100
receiver_y = 200
receiver_z = 300

# 卫星坐标
satellite1_x = 400
satellite1_y = 500
satellite1_z = 600

satellite2_x = 700
satellite2_y = 800
satellite2_z = 900

# 计算接收器到卫星的距离
distance_to_satellite1 = math.sqrt((receiver_x - satellite1_x)**2 + (receiver_y - satellite1_y)**2 + (receiver_z - satellite1_z)**2)
distance_to_satellite2 = math.sqrt((receiver_x - satellite2_x)**2 + (receiver_y - satellite2_y)**2 + (receiver_z - satellite2_z)**2)

# 根据距离和卫星位置，解出接收器坐标
# ... (省略解方程过程)

### 6.2 机器人定位和路径规划

在机器人定位和路径规划中，笛卡尔坐标系用于描述机器人的位置和运动。通过传感器和定位算法，机器人可以确定其在环境中的坐标。

graph LR
subgraph 机器人定位
    start(机器人) --> pos(位置)
    pos --> end(已定位)
end

subgraph 路径规划
    start(起点) --> path(路径)
    path --> end(终点)
end

### 6.3 医学成像和诊断

在医学成像和诊断中，笛卡尔坐标系用于描述和分析患者的解剖结构。例如，在CT扫描中，患者被放置在扫描仪中，而X射线束从不同角度穿过患者。通过处理这些X射线数据，可以生成患者身体的横断面图像。

# CT扫描图像数据
image_data = [
    [10, 20, 30, 40, 50],
    [60, 70, 80, 90, 100],
    [110, 120, 130, 140, 150],
    [160, 170, 180, 190, 200],
    [210, 220, 230, 240, 250],
]

# 提取患者心脏区域的数据
heart_region = image_data[1:4, 1:4]

# 分析心脏区域的密度分布
# ... (省略分析过程)