笛卡尔坐标系中的傅里叶级数：公式、性质、应用，一文掌握

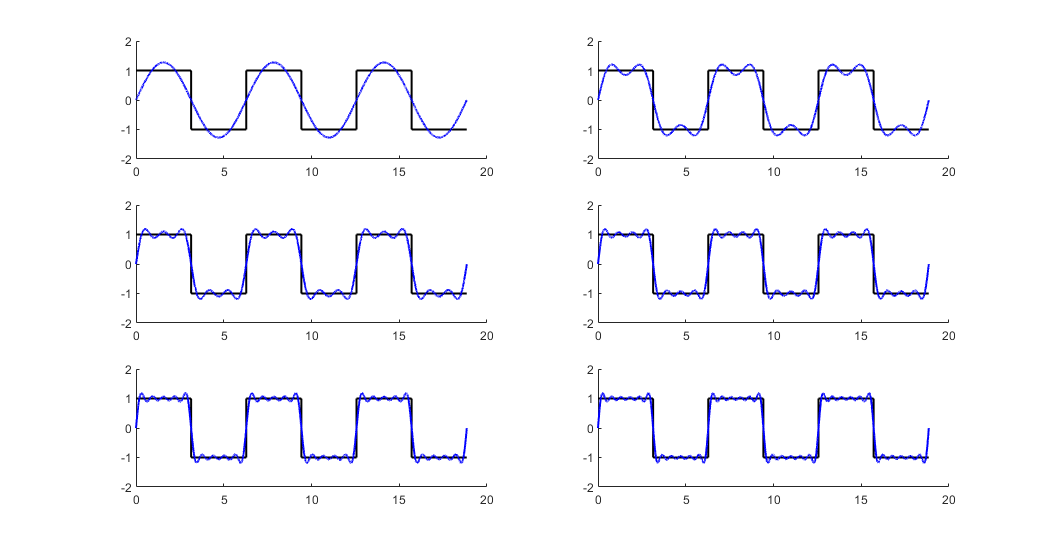
# 1. 笛卡尔坐标系中的傅里叶级数简介

傅里叶级数是数学中一种重要的工具，用于将周期函数分解为正弦和余弦函数的无穷级数。它在信号处理、物理学和许多其他领域都有广泛的应用。

在笛卡尔坐标系中，傅里叶级数可以表示为：

f(x) = a_0/2 + ∑[a_n cos(nπx/L) + b_n sin(nπx/L)]

其中：

* `f(x)` 是要展开的周期函数
* `a_0`、`a_n` 和 `b_n` 是傅里叶系数
* `L` 是函数的周期

# 2. 傅里叶级数的理论基础

### 2.1 傅里叶级数的定义和性质

#### 2.1.1 傅里叶级数的定义

傅里叶级数是一种将周期函数表示为三角函数级数的数学工具。对于一个周期为 `2π` 的函数 `f(x)`，其傅里叶级数表示为：

f(x) = a_0 + Σ[a_n cos(nx) + b_n sin(nx)]

其中，`a_0` 为常数项，`a_n` 和 `b_n` 为傅里叶系数。

#### 2.1.2 傅里叶级数的收敛性

傅里叶级数的收敛性取决于函数 `f(x)` 的性质。对于连续且分段光滑的函数，其傅里叶级数在每个点都收敛到函数值。对于不连续的函数，傅里叶级数可能在不连续点处出现吉布斯现象，即级数收敛到函数的平均值。

### 2.2 正交函数系和傅里叶系数

#### 2.2.1 正交函数系的概念

正交函数系是指一组在指定区间内正交的函数。对于区间 `[0, 2π]` 上的三角函数系，其正交性可以表示为：

∫[0, 2π] cos(mx) cos(nx) dx = 0, m ≠ n
∫[0, 2π] sin(mx) sin(nx) dx = 0, m ≠ n
∫[0, 2π] cos(mx) sin(nx) dx = 0, ∀m, n

#### 2.2.2 傅里叶系数的计算

傅里叶系数可以通过以下公式计算：

a_0 = (1/π) ∫[0, 2π] f(x) dx
a_n = (1/π) ∫[0, 2π] f(x) cos(nx) dx
b_n = (1/π) ∫[0, 2π] f(x) sin(nx) dx

这些公式利用了三角函数系的正交性，将函数 `f(x)` 投影到正交基底上，从而得到傅里叶系数。

# 3.1 傅里叶级数在信号处理中的应用

傅里叶级数在信号处理中有着广泛的应用，它可以将一个时域信号分解成一系列正弦和余弦分量，从而方便地对信号进行分析和处理。

**3.1.1 信号的傅里叶变换**

信号的傅里叶变换是将时域信号转换为频域信号的过程，它通过傅里叶级数来实现。设时域信号为 \(x(t)\)，其傅里叶变换为 \(X(f)\)，则有：

import numpy as np

def fourier_transform(x, fs):
  """
  计算信号的傅里叶变换。

  参数：
    x: 时域信号。
    fs: 采样频率。

  返回：
    X: 频域信号。
  """

  N = len(x)
  k = np.arange(N)
  T = N / fs
  freq = k / T
  X = np.fft.fft(x) / N
  return freq, X

**代码逻辑逐行解读：**

1. 导入NumPy库。
2. 定义傅里叶变换函数，输入参数为时域信号和采样频率。
3. 计算信号长度和采样周期。
4. 计算频率数组。
5. 使用NumPy的傅里叶变换函数计算频域