时间序列分析中的PCA降维：数据降维新利器，预测更精准

# 1. 时间序列分析与PCA降维概述

时间序列分析是处理随时间变化的数据的统计技术。它广泛应用于金融、气象、医疗等领域。然而，高维时间序列数据会带来计算复杂度高、模型难以解释等问题。

PCA（主成分分析）是一种降维技术，它通过线性变换将高维数据投影到低维空间中，同时最大化数据方差。PCA降维可以有效减少数据维度，降低计算复杂度，提高模型可解释性。

# 2. PCA降维理论基础

### 2.1 PCA原理与数学推导

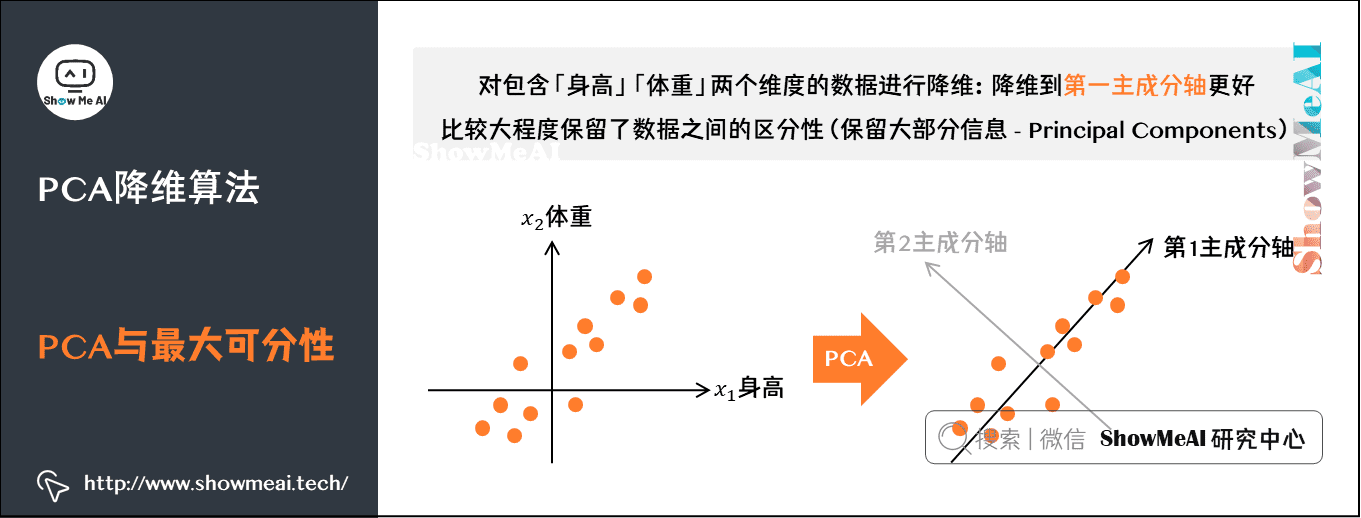
**PCA原理**

主成分分析（PCA）是一种无监督降维技术，其目的是将高维数据投影到低维空间中，同时保留尽可能多的原始数据信息。PCA的原理是通过寻找原始数据中方差最大的方向，并沿这些方向投影数据。

**数学推导**

假设原始数据为`X`，是一个`n x p`矩阵，其中`n`为样本数量，`p`为特征数量。PCA的数学推导如下：

1. **标准化数据：**对数据进行标准化，使每个特征的均值为0，方差为1。
2. **计算协方差矩阵：**计算`X`的协方差矩阵`C`，其元素`C[i, j]`表示特征`i`和`j`之间的协方差。
3. **特征值分解：**对协方差矩阵`C`进行特征值分解，得到特征值`λ`和特征向量`v`。
4. **选择主成分：**选择特征值最大的`k`个特征向量，形成投影矩阵`P`，其中`P`的列向量为`k`个主成分。
5. **投影数据：**将原始数据`X`投影到低维空间，得到降维后的数据`Y`：

Y = X @ P

### 2.2 PCA的优缺点分析

**优点：**

* **信息保留：**PCA可以有效保留原始数据中的重要信息，减少数据维度。
* **计算简单：**PCA的计算过程相对简单，易于实现。
* **可解释性：**PCA的主成分具有物理意义，可以帮助理解数据的结构。

**缺点：**

* **线性假设：**PCA假设数据分布是线性的，对于非线性数据可能效果不佳。
* **方差损失：**PCA会损失原始数据中方差较小的信息，可能影响数据的准确性。
* **主成分选择：**选择主成分的数量需要经验或试错，可能影响降维效果。

# 3. PCA降维实践应用

### 3.1 PCA降维流程与实现

PCA降维的流程主要分为以下几个步骤：

1. **数据标准化：**将原始数据进行标准化处理，消除不同特征量纲的影响，确保各特征处于同一数量级。
2. **计算协方差矩阵：**计算原始数据协方差矩阵，反映各特征之间的相关性。
3. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。特征值代表了各主成分的方差贡献度，特征向量代表了各主成分的方向。
4. **主成分选择：**根据特征值的大小，选择保留的主成分个数。通常选择方差贡献度较大的主成分，以保留原始数据中的大部分信息。
5. **数据投影：**将原始数据投影到选定的主成分上，得到降维后的数据。

在Python中，可以使用`sklearn.decom