经济学中的PCA降维：经济指标降维新视角，预测更准确

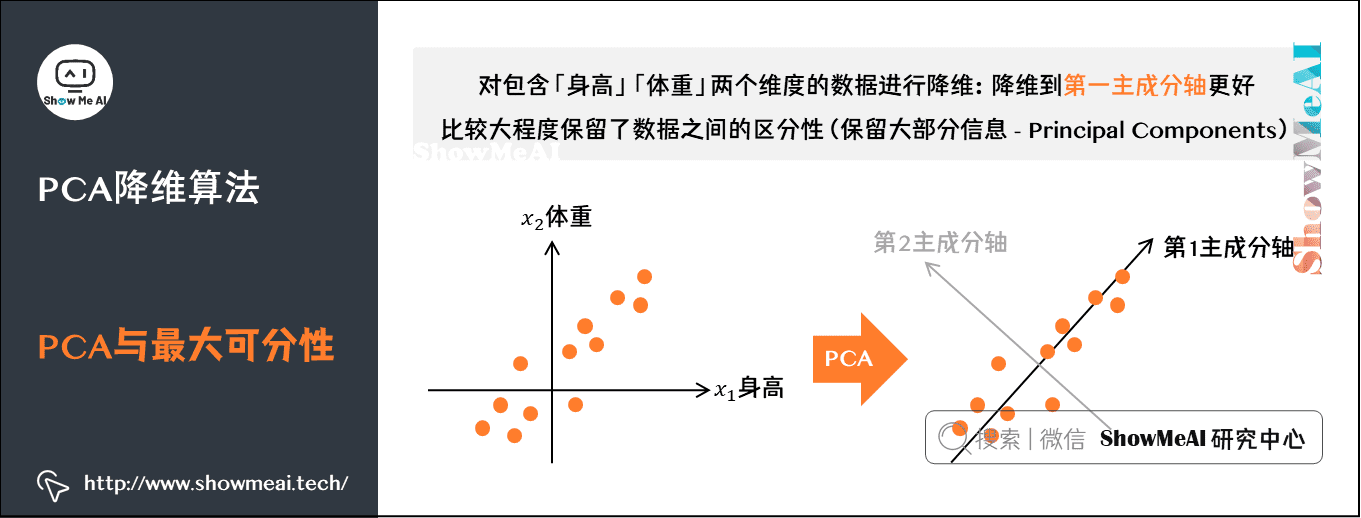
# 1. 经济学中的降维理论

降维理论在经济学中是一种重要的分析工具，它通过将高维数据降维到低维空间，简化数据的复杂性，提取数据的关键特征。降维理论的应用可以帮助经济学家深入理解经济现象，提高经济预测和风险管理的准确性。

降维理论的核心思想是通过线性变换，将高维数据投影到低维空间，使得低维数据保留了高维数据中最重要的信息。降维算法有很多种，其中最常用的算法之一是主成分分析（PCA）。PCA算法通过计算协方差矩阵的特征值和特征向量，提取数据中的主成分，并对主成分进行降维。

# 2. PCA降维算法在经济学中的应用

### 2.1 PCA降维算法原理

#### 2.1.1 协方差矩阵和特征值分解

PCA降维算法的基础是协方差矩阵。协方差矩阵描述了不同变量之间的相关性，元素为各个变量的协方差。对于一个包含n个变量的数据集，其协方差矩阵为：

Cov = 1/(n-1) * (X - X_mean).T * (X - X_mean)

其中，X为原始数据集，X_mean为数据集的均值。

协方差矩阵是一个对称矩阵，其特征值和特征向量可以用来进行降维。特征值表示了协方差矩阵中各个主成分的方差，特征向量表示了主成分的方向。

#### 2.1.2 主成分的提取和降维

PCA降维算法通过特征值分解来提取数据集的主成分。主成分是原始变量的线性组合，其方差最大，并且与其他主成分正交。

提取主成分的步骤如下：

1. 计算协方差矩阵Cov。
2. 对协方差矩阵进行特征值分解，得到特征值和特征向量。
3. 根据特征值的大小对特征向量进行排序。
4. 选择前k个特征向量，其中k为降维后的维度。

前k个特征向量组成的矩阵称为主成分加载矩阵，它将原始数据集投影到主成分空间。原始数据集中的每个样本点都可以表示为：

Z = X * P

其中，Z为降维后的数据集，P为主成分加载矩阵。

### 2.2 PCA降维算法在经济学中的实践

#### 2.2.1 经济指标选择与预处理

在经济学中应用PCA降维算法时，首先需要选择合适的经济指标。这些指标应能反映经济活动的各个方面，并且具有较高的相关性。

常用的经济指标包括：GDP、CPI、PPI、失业率、利率、汇率等。在选择指标时，需要考虑指标的时效性、可靠性和可获得性。

选择指标后，需要对数据进行预处理，包括缺失值处理、异常值处理和标准化。缺失值处理可以通过插值或删除来完成。异常值处理可以通过Winsorize或删除来完成。标准化可以消除不同指标单位和量纲的影响。

#### 2.2.2 PCA降维模型的构建和评估

构建PCA降维模型需要确定降维后的维度。维度选择可以根据以下原则：

* 方差贡献率：选择方差贡献率累积超过85%的维度。
* 奇异值：选择奇异值大于1的维度。
* 业务需求：根据实际业务需求选择维度。

确定维度后，就可以构建PCA降维模型。模型构建步骤如下：

1. 计算协方差矩阵。
2. 对协方差矩阵进行特征值分解。
3. 根据维度选择特征向量。
4. 构建主成分加载矩阵。

模型构建完成后，需要对模型进行评估。评估指标包括：

* 方差贡献率：降维后主成分的方差贡献率。
* 累积方差贡献率：降维后主成分的累积方差贡献率。
* 奇异值：降维后主成分的奇异值