【PCA降维秘籍】：揭秘数据降维的10大实战应用

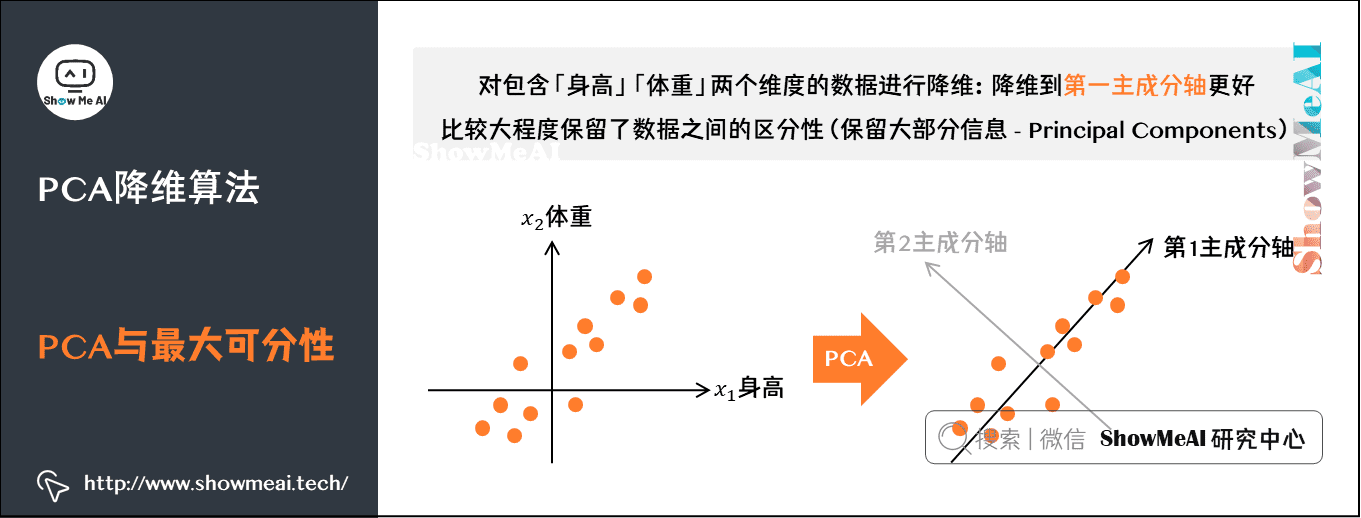
# 1. PCA降维概述

主成分分析（PCA）是一种广泛应用于降维的经典算法。它通过线性变换将高维数据投影到低维空间，同时保留数据的关键信息。PCA的本质是找到数据中方差最大的方向，这些方向称为主成分。

PCA在数据分析和机器学习中有着广泛的应用。它可以用于图像压缩、文本主题提取、数据可视化、机器学习中的特征提取和深度学习中的数据预处理等。

# 2. PCA降维算法原理

PCA降维是一种线性降维技术，其核心思想是将原始数据投影到一个低维子空间中，使得投影后的数据方差最大化。这一过程涉及以下几个关键步骤：

### 2.1 PCA降维的数学基础

#### 2.1.1 协方差矩阵和特征值分解

协方差矩阵是一个对称矩阵，其元素表示不同特征之间协方差的大小。协方差矩阵的特征值分解可以得到一组特征值和特征向量。特征值表示协方差矩阵中方差最大的方向，而特征向量则表示这些方向。

#### 2.1.2 主成分分析的几何解释

主成分分析可以从几何角度理解。原始数据在高维空间中形成一个数据点云。PCA降维的过程就是将数据点云投影到一个低维子空间中，使得投影后的数据点方差最大化。投影后的方向就是主成分。

### 2.2 PCA降维的算法流程

#### 2.2.1 数据标准化和中心化

在进行PCA降维之前，需要对原始数据进行标准化和中心化处理。标准化将数据缩放到一个统一的范围，而中心化将数据平移到原点。这些操作可以提高PCA算法的稳定性和准确性。

#### 2.2.2 协方差矩阵计算

根据标准化和中心化后的数据计算协方差矩阵。协方差矩阵的元素表示不同特征之间协方差的大小。

#### 2.2.3 特征值和特征向量求解

对协方差矩阵进行特征值分解，得到一组特征值和特征向量。特征值表示协方差矩阵中方差最大的方向，而特征向量则表示这些方向。

import numpy as np
from sklearn.decomposition import PCA

# 原始数据
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 数据标准化和中心化
X_std = (X - np.mean(X)) / np.std(X)

# 协方差矩阵计算
cov_matrix = np.cov(X_std.T)

# 特征值和特征向量求解
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

# 特征值排序，降序排列
eigenvalues_sorted = np.argsort(eigenvalues)[::-1]

# 特征向量按特征值排序
eigenvectors_sorted = eigenvectors[:, eigenvalues_sorted]

# 主成分矩阵
principal_components = eigenvectors_sorted[:, :2]

# 数据投影
X_pca = np.dot(X_std, principal_components)

**代码逻辑逐行解读：**

* 第 4 行：导入必要的库。
* 第 6-8 行：生成原始数据。
* 第 10-12 行：对数据进行标准化和中心化处理。
* 第 14-16 行：计算协方差矩阵。
* 第 18-20 行：对协方差矩阵进行特征值分解，得到特征值和特征向量。
* 第 22-24 行：对特征值进行排序，降序排列。
* 第 26 行：对特征向量按特征值排序。
* 第 28 行：得到主成分矩阵，包含前两个主成分。
* 第 30 行：将数据投影到主成分矩阵上，得到降维后的数据。

**参数说明：**

* `X`：原始数据。
* `X_std`：标准化和中心化后的数据。
* `cov_matrix`：协方差矩阵。
* `eigenvalues`：特征值。
* `eigenvectors`：特征向量。
* `eigenvalues_sorted`：排序后的特征值。
* `eigenvectors_sorted`：按特征值排序后的特征向量。
* `principal_components`：主成分矩阵。
* `X_pca`：降维后的数据。

# 3.1 图像降维与压缩

#### 3.1.1 PCA降维在图像处理中的原理

图像降维是利用PCA将高维图像数据投影到低维空间，从而减少图像数据量，同时保留图像的主要特征。其原理如下：

- **数据标准化和中心化：**将图像数据进行标准化和中心化，消除不同像素值之间的差异，使数据分布更均匀。
- **协方差矩阵计算：**计算图像数据的协方差矩阵，反映图像数据各像素之间的相关性。
- **特征值和特征向量求解：**对协方差矩阵进行特征值分解，得到一组特征值和对应的特征向量。特征值代表图像数据各主成分的方差，特征向量代表主成分的方向。
- **降维投影：**将图像数据投影到由前k个特征向量组成的低维空间中，k值代表降维后的维度。

#### 3.1.2 PCA降维的图像压缩示例

使用PCA进行图像压缩的步骤如下：

1. **读取图像：**读取原始图像数据。
2. **数据预处理：**对图像数据进行标准化和中心化。
3. **PCA降维：**计算协方差矩阵，求解特征值和特征向量，将图像数据投影到低维空间中。
4. **图像重建：**使用前k个特征向量将降维后的数据投影回原始空间，得到压缩后的图像。

import numpy as np
from sklearn.decomposition import PCA

# 读取图像
image = cv2.imread('image.jpg')

# 数据预处理
image_data = image.reshape(-1, 3)  # 将图像展平为一维数组
image_data_std = (image_data - np.mean(image_data)) / np.std(image_data)  # 标准化和中心化

# PCA降维
pca = PCA(n_components=100)  # 降维到100维
image_data_pca = pca.fit_transform(image_data_std)

# 图像重建
image_reconstructed = pca.inverse_transform(image_data_pca)

# 保存压缩后的图像
cv2.imwrite('image_compressed.jpg', image_reconstructed.reshape(image.shape))

### 3.2 文本降维与主题提取

#### 3.2.1 PCA降维在文本挖掘中的原理

文本降维是利用PCA将高维文本数据投影到低维空间，从而提取文本的主要主题。其原理与图像降维类似：

- **文本向量化：**将文本数据转换为词频-逆文档频率（TF-IDF）矩阵，每个单词对应一个维度。
- **数据标准化和中心化：**对TF-IDF矩阵进行标准化和中心化。
- **协方差矩阵计算：**计算TF-IDF矩阵的协方差矩阵，反映单词之间的相关性。
- **特征值和特征向量求解：**对协方差矩阵进行特征值分解，得到一组特征值和对应的特征向量。特征值代表文本数据各主成分的方差，特征向量代表主成分的方向。
- **降维投影：**将文本数据投影到由前k个特征向量组成的低维空间中，k值代表降维后的维度。

#### 3.2.2 PCA降维的文本主题提取示例

使用PCA进行文本主题提取的步骤如下：

1. **读取文本：**读取文本数据。
2. **文本向量化：**将文本数据转换为TF-IDF矩阵。
3. **数据预处理：**对TF-IDF矩阵进行标准化和中心化。
4. **PCA降维：**计算协方差矩阵，求解特征值和特征向量，将文本数据投影到低维空间中。
5. **主题提取：**分析低维空间中的特征向量，提取文本的主要主题。

import numpy as np
from sklearn.decomposition import PCA
from sklearn.feature_extraction.text import TfidfVectorizer

# 读取文本
with open('text.txt', 'r') as f:
    text = f.read()

# 文本向量化
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform([text])

# 数据预处理
X_std = (X - np.mean(X)) / np.std(X)

# PCA降维
pca = PCA(n_components=10)
X_pca = pca.fit_transform(X_std)

# 主题提取
print("前10个主成分：")
for i in range(10):
    print(f"主成分{i+1}：{vectorizer.get_feature_names_out()[np.argsort(pca.components_[i])[-10:]]}")

# 4. PCA降维进阶应用

### 4.1 PCA降维与机器学习

#### 4.1.1 PCA降维在机器学习中的原理

PCA降维在机器学习中主要用于特征工程，通过降低特征维数来提升机器学习模型的性能。其原理如下：

1. **数据预处理：**将原始数据标准化和中心化，消除特征之间的量纲差异和均值影响。
2. **协方差矩阵计算：**计算原始数据协方差矩阵，反映特征之间的相关性。
3. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. **主成分选择：**根据特征值的大小，选择具有较高方差的主成分，形成新的低维特征空间。

#### 4.1.2 PCA降维的机器学习应用示例

PCA降维在机器学习中广泛应用于：

- **特征选择：**去除冗余和无关特征，提高模型泛化能力。
- **数据降维：**降低数据维数，减少计算量和存储空间。
- **异常检测：**通过低维特征空间中的异常点识别异常样本。

### 4.2 PCA降维与深度学习

#### 4.2.1 PCA降维在深度学习中的原理

PCA降维在深度学习中主要用于数据预处理和特征提取。其原理与机器学习中类似，但由于深度学习模型的复杂性，PCA降维在深度学习中的应用更为广泛。

1. **数据预处理：**将原始数据标准化和中心化，消除特征之间的量纲差异和均值影响。
2. **协方差矩阵计算：**计算原始数据协方差矩阵，反映特征之间的相关性。
3. **特征值分解：**对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. **主成分选择：**根据特征值的大小，选择具有较高方差的主成分，形成新的低维特征空间。
5. **深度学习模型训练：**将低维特征空间作为深度学习模型的输入，进行模型训练。

#### 4.2.2 PCA降维的深度学习应用示例

PCA降维在深度学习中广泛应用于：

- **图像降维：**降低图像维数，减少计算量和存储空间。
- **文本降维：**降低文本维数，提取文本特征和主题。
- **自然语言处理：**降低自然语言数据的维数，提高模型性能。

# 5. PCA降维的优缺点与适用场景

### 5.1 PCA降维的优点

PCA降维作为一种经典的降维算法，具有以下优点：

- **线性变换：**PCA降维是一种线性变换，它将原始数据投影到一个新的正交基上，从而降低数据的维度。这种线性变换易于理解和实现。
- **信息保留：**PCA降维通过最大化方差来选择主成分，从而最大程度地保留原始数据中的信息。
- **计算效率：**PCA降维算法的计算效率较高，特别是对于大数据集，它可以快速有效地进行降维。
- **可解释性：**PCA降维的主成分具有明确的物理意义，它们代表了原始数据中方差最大的方向，便于理解和解释。

### 5.2 PCA降维的缺点

尽管PCA降维具有诸多优点，但它也存在一些缺点：

- **不适用于非线性数据：**PCA降维是一种线性算法，它假设数据是线性可分的。对于非线性数据，PCA降维可能无法有效地降低维度。
- **维度选择困难：**PCA降维需要选择保留的主成分数目。这个选择过程通常是经验性的，并且没有明确的准则。
- **信息损失：**PCA降维在降低维度时不可避免地会损失一些信息。如果保留的主成分数目太少，可能会导致原始数据中重要信息的丢失。
- **对异常值敏感：**PCA降维对异常值比较敏感。异常值可能会对协方差矩阵的计算产生影响，从而导致主成分分析的结果失真。

### 5.3 PCA降维的适用场景

PCA降维广泛应用于各种领域，包括：

- **图像处理：**图像降维可以减少图像文件的大小，同时保留图像的主要特征。
- **文本挖掘：**文本降维可以提取文本中的主题和关键词，用于文本分类和聚类。
- **数据可视化：**PCA降维可以将高维数据投影到低维空间，便于数据可视化和分析。
- **机器学习：**PCA降维可以作为机器学习算法的预处理步骤，减少特征数目，提高算法的效率和准确性。
- **深度学习：**PCA降维可以作为深度学习模型的输入，减少模型的复杂性和训练时间。

# 6. PCA降维的局限性和发展趋势

### 局限性

尽管PCA降维是一种强大的降维技术，但它也存在一些局限性：

- **线性假设：**PCA降维假设数据在特征空间中呈线性分布。如果数据是非线性的，PCA降维的效果可能会不理想。
- **信息损失：**PCA降维通过投影数据到低维子空间来减少维度。然而，这种投影不可避免地会导致信息损失。
- **主观性：**PCA降维的降维结果取决于所选择的特征。不同的特征选择策略可能会产生不同的降维结果。
- **高计算成本：**对于大型数据集，PCA降维的计算成本可能很高，尤其是当特征数量很大时。

### 发展趋势

为了克服PCA降维的局限性，研究人员正在探索各种改进方法，包括：

- **非线性PCA：**这些方法将非线性映射应用于数据，以将其转换为线性可分的形式，然后应用PCA降维。
- **稀疏PCA：**这些方法通过引入稀疏性约束来选择特征，从而减少信息损失和提高计算效率。
- **局部PCA：**这些方法将数据划分为局部子空间，并在每个子空间上应用PCA降维，从而处理非线性数据。
- **流式PCA：**这些方法允许在数据流式传输时进行实时PCA降维，从而处理大规模数据集。