PCA与因子分析：兄弟相争，各显神通，带你领略降维新境界

# 1. PCA与因子分析：概念与原理**

**1.1 PCA与因子分析概述**

主成分分析（PCA）和因子分析是两种密切相关的多变量统计技术，用于分析高维数据集。PCA旨在通过识别数据集中的主要变异方向来减少数据的维度，而因子分析则旨在识别潜在的潜在变量或因素，这些变量或因素解释了观测变量之间的协方差。

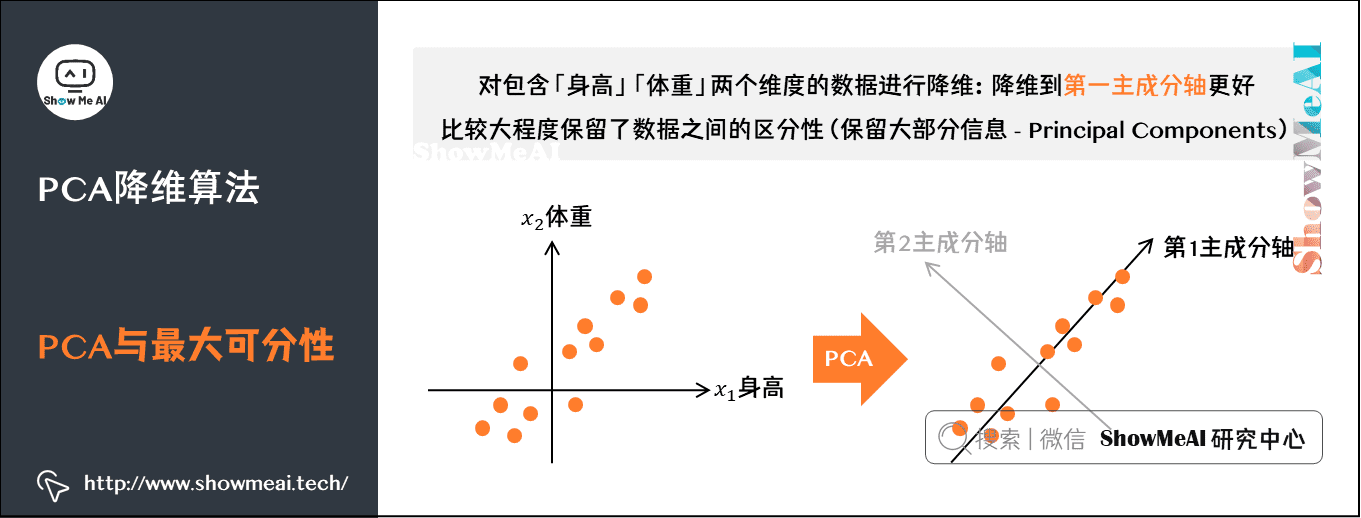
**1.2 PCA的基本原理**

PCA的基本原理是将原始数据集投影到一个新的正交坐标系上，其中前几个主成分捕获了数据集中的最大方差。主成分是原始变量的线性组合，按其方差从大到小排列。

# 2.1 PCA的基本原理和算法

### 2.1.1 主成分分析的数学原理

主成分分析（PCA）是一种无监督降维技术，其目标是将高维数据投影到低维空间中，同时最大化投影数据的方差。PCA的数学原理基于以下步骤：

1. **数据中心化：**将数据集中每个特征减去其均值，以消除特征之间的尺度差异。
2. **协方差矩阵计算：**计算中心化数据的协方差矩阵，该矩阵表示特征之间的相关性。
3. **特征值和特征向量计算：**对协方差矩阵进行特征分解，得到一组特征值和相应的特征向量。
4. **主成分选择：**选择具有最大特征值的特征向量，这些特征向量代表了数据集中最大的方差方向。
5. **数据投影：**将数据投影到由主成分组成的低维空间中。

### 2.1.2 PCA算法的实现和应用

PCA算法的实现通常涉及以下步骤：

import numpy as np
from sklearn.decomposition import PCA

# 数据中心化
data = data - np.mean(data, axis=0)

# 协方差矩阵计算
cov_matrix = np.cov(data)

# 特征值和特征向量计算
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

# 主成分选择
num_components = 2  # 选择前两个主成分
principal_components = eigenvectors[:, :num_components]

# 数据投影
projected_data = np.dot(data, principal_components)

**代码逻辑分析：**

* `data`是需要进行PCA的原始数据。
* `np.mean(data, axis=0)`计算每一列的均值，并从原始数据中减去，实现数据中心化。
* `np.cov(data)`计算协方差矩阵。
* `np.linalg.eig(cov_matrix)`计算特征值和特征向量。
* `eigenvectors[:, :num_components]`选择前`num_components`个特征向量作为主成分。
* `np.dot(data, principal_components)`将数据投影到主成分组成的低维空间。

**参数说明：**

* `num_components`：要提取的主成分的数量。

**应用示例：**

PCA广泛应用于各种领域，包括：

* **图像处理：**图像压缩、人脸识别
* **文本挖掘：**文本分类、主题建模
* **金融分析：**股票市场预测、风险管理
* **生物信息学：**基因表达分析、疾病诊断

# 3. 因子分析的理论与实践

### 3.1 因子分析的基本原理和模型

#### 3.1.1 因子分析的数学模型

因子分析是一种多变量统计技术，旨在从一组观察变量中识别出潜在的、不可观测的因子。其基本数学模型可以表示为：

X = ΛF + ε

其中：

* **X** 是观测变量矩阵，包含了观测到的变量值
* **Λ** 是因子载荷矩阵，