堆排序算法的改进算法：探索堆排序的优化方向，提升算法效率

# 1. 堆排序算法概述

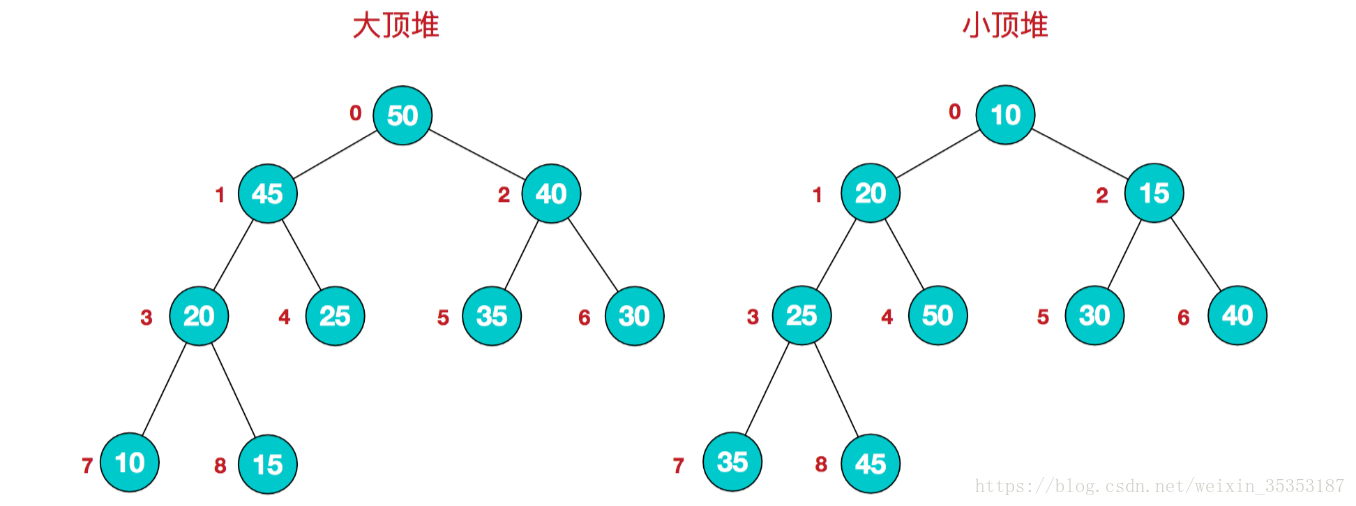
堆排序是一种基于堆数据结构的排序算法。堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆排序通过将输入数组转换为堆，然后通过重复交换堆顶元素和最后一个元素并重新堆化来实现排序。

堆排序算法具有以下优点：

* 时间复杂度为 O(n log n)，无论输入数组的初始顺序如何。
* 空间复杂度为 O(1)，因为它不需要额外的空间来存储中间结果。
* 算法简单易懂，实现起来相对容易。

# 2. 堆排序算法的改进算法

### 2.1 基于堆的高度优化

#### 2.1.1 二叉堆的性质和构建

二叉堆是一种完全二叉树，满足以下性质：

- **堆序性：**每个节点的值都大于或等于其子节点的值。
- **完全性：**除了最后一层之外，所有层都完全填充。

构建二叉堆可以通过自底向上或自顶向下的方法。自底向上方法从最底层开始，逐层向上调整堆序性；自顶向下方法从根节点开始，逐层向下调整堆序性。

#### 2.1.2 堆的高度优化策略

堆的高度直接影响堆排序的时间复杂度。为了优化堆的高度，可以采用以下策略：

- **平衡因子：**对每个节点计算其平衡因子，即左子树的高度减去右子树的高度。如果平衡因子大于 1 或小于 -1，则需要进行旋转操作。
- **旋转操作：**旋转操作可以将不平衡的子树调整为平衡状态。有左旋和右旋两种旋转操作，具体操作如下：

def left_rotate(node):
    """
    对节点 node 进行左旋操作。

    参数：
        node: 需要旋转的节点。

    返回：
        旋转后的节点。
    """
    right_child = node.right_child
    node.right_child = right_child.left_child
    right_child.left_child = node

    return right_child


def right_rotate(node):
    """
    对节点 node 进行右旋操作。

    参数：
        node: 需要旋转的节点。

    返回：
        旋转后的节点。
    """
    left_child = node.left_child
    node.left_child = left_child.right_child
    left_child.right_child = node

    return left_child

### 2.2 基于交换次数优化

#### 2.2.1 堆排序的交换次数分析

堆排序的交换次数与堆的高度和数据分布有关。在最坏情况下，堆排序需要进行 O(n log n) 次交换。

#### 2.2.2 减少交换次数的优化方法

为了减少交换次数，可以采用以下优化方法：

- **堆排序变种：**有几种堆排序变种可以减少交换次数，如霍夫曼堆排序、弗洛伊德堆排序等。
- **局部排序：**在堆排序过程中，可以对局部有序的数据进行局部排序，减少交换次数。
- **插入排序：**当堆的大小较小时，可以使用插入排序来代替堆排序，减少交换次数。

### 2.3 基于数据结构优化

#### 2.3.1 斐波那契堆

斐波那契堆是一种基于斐波那契数列的堆数据结构。与二叉堆相比，斐波那契堆具有以下优点：

- **更低的时间复杂度：**斐波那契堆的合并操作时间复杂度为 O(log n)，而二叉堆的合并操作时间复杂度为 O(n)。
- **更小的常数因子：**斐波那契堆的常数因子比二叉堆更小，因此在实际应用中效率更高。

#### 2.3.2 二项堆

二项堆是一种基于二项树的堆数据结构。与斐波那契堆相比，二项堆具有以下优点：

- **更简单的实现：**二项堆的实现比斐波那契堆更简单，更容易理解和维护。
- **更好的空间效率：**二项堆的空间效率比斐波那契堆更好，在内存受限的场景下更适合使用。

# 3.1 堆排序在数据分析中的应用

#### 3.1.1 数据排序和统计

堆排序在数据分析中的一项重要应用是数据排序和统计。在数据分