堆排序在算法竞赛中的应用：掌握堆排序在竞赛中的制胜法宝，提升算法能力

# 1. 堆排序的理论基础**

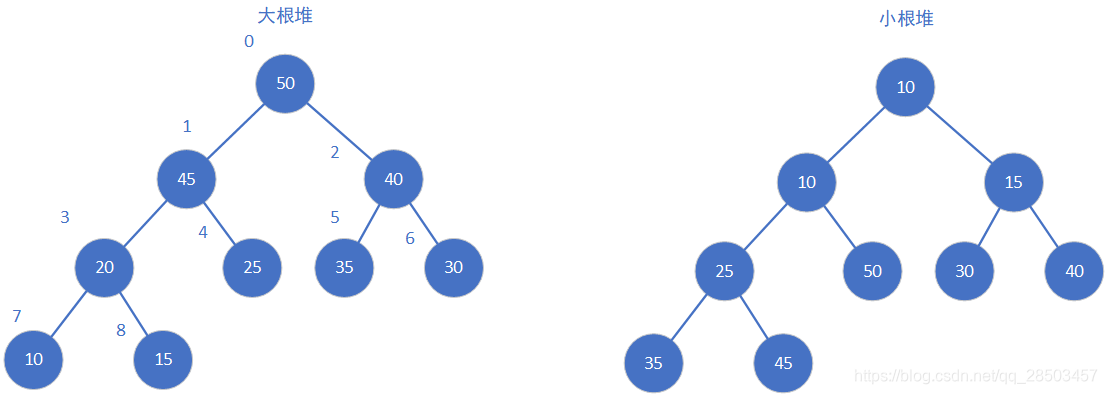
堆排序是一种基于堆数据结构的排序算法。堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆排序的原理是将待排序的数组构建成一个堆，然后依次从堆顶弹出最大（或最小）的元素，直到堆为空。

堆排序的时间复杂度为 O(n log n)，其中 n 为待排序数组的长度。堆排序的优点在于其稳定的时间复杂度，即使对于已经排序或部分排序的数组，其时间复杂度也不会发生变化。

# 2. 堆排序的实践技巧**

堆排序是一种高效的排序算法，在算法竞赛中有着广泛的应用。本章节将深入探讨堆排序的实践技巧，包括堆的构建和维护，以及堆排序的算法流程。

## 2.1 堆的构建和维护

### 2.1.1 最大堆和最小堆的定义

堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值（最大堆）或小于或等于其子节点的值（最小堆）。

### 2.1.2 堆的插入和删除操作

**插入操作：**

1. 将新元素插入到二叉树的最后一个叶子节点。
2. 与其父节点比较，如果满足堆的性质，则停止。
3. 否则，交换新元素与其父节点，并重复步骤 2。

**删除操作：**

1. 将根节点与最后一个叶子节点交换。
2. 删除最后一个叶子节点。
3. 从根节点开始，与左右子节点比较，交换较大的（或较小的）子节点，并重复步骤 3。

## 2.2 堆排序的算法流程

### 2.2.1 堆排序的步骤

1. 将待排序的数组构建成一个最大堆。
2. 将堆顶元素与最后一个元素交换。
3. 将堆顶元素弹出，并重新调整堆的结构。
4. 重复步骤 2 和 3，直到堆中只剩一个元素。

### 2.2.2 堆排序的时间复杂度分析

堆排序的时间复杂度为 O(n log n)，其中 n 为待排序数组的长度。

**代码块：**

def heap_sort(arr):
    """堆排序算法

    Args:
        arr (list): 待排序的数组
    """

    # 构建最大堆
    for i in range(len(arr) // 2 - 1, -1, -1):
        max_heapify(arr, i, len(arr))

    # 堆排序
    for i in range(len(arr) - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        max_heapify(arr, 0, i)

def max_heapify(arr, i, n):
    """维护最大堆性质

    Args:
        arr (list): 待维护的数组
        i (int): 当前节点的索引
        n (int): 数组的长度
    """

    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:
        largest = left

    if right < n and arr[right] > arr[largest]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        max_heapify(arr, largest, n)

**逻辑分析：**

- `heap_sort` 函数接收一个数组 `arr`，并对其进行堆排序。
- `max_heapify` 函数维护最大堆的性质，确保每个节点的值都大于或等于其子节点的值。
- 在堆排序过程中，`max_heapify` 函数不断维护堆的性质，同时将堆顶元素与最后一个元素交换，从而实现排序。

**参数说明：**

- `arr`：待排序的数组。
- `i`：当前节点的索引。
- `n`：数组的长度。

# 3.1 堆排序在数据结构竞赛中的运用

#### 3.1.1 求中位数

在数据结构竞赛中，经常会遇到需要求解数据流中位数的问题。中位数是指一个序列中所有元素按升序排列后的中间值。对于偶数个元素的序列，中位数为中间两个元素的平均值。

使用堆排序可以高效地求解中位数。具体做法是维护两个堆：最大堆和小根堆。最大堆存储序列中较小的元素，小根堆存储序列中较大的元素。当序列中元素个数为偶数时，中位数为两个堆顶元素的平均值；当序列中元素个数为奇数时，中位数为最大堆的堆顶元素。

import heapq

class MedianFinder:

    def __init__(self):
        self.max_heap = []  # 最大堆，存储较小的元素
        self.min_heap = []  # 小根堆，存储较大的元素

    def add_num(self, num):
        # 将 num 插入到最大堆中
        heapq.heappush(self.max_heap, -num)

        # 如果最大堆中的元素个数大于小根堆中的元素个数，则将最大堆的堆顶元素弹出并插入到小根堆中
        if len(self.max_heap) > len(self.min_heap):
            heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap))

    def find_median(self):