堆排序时间复杂度分析：揭示堆排序效率之谜，优化算法性能

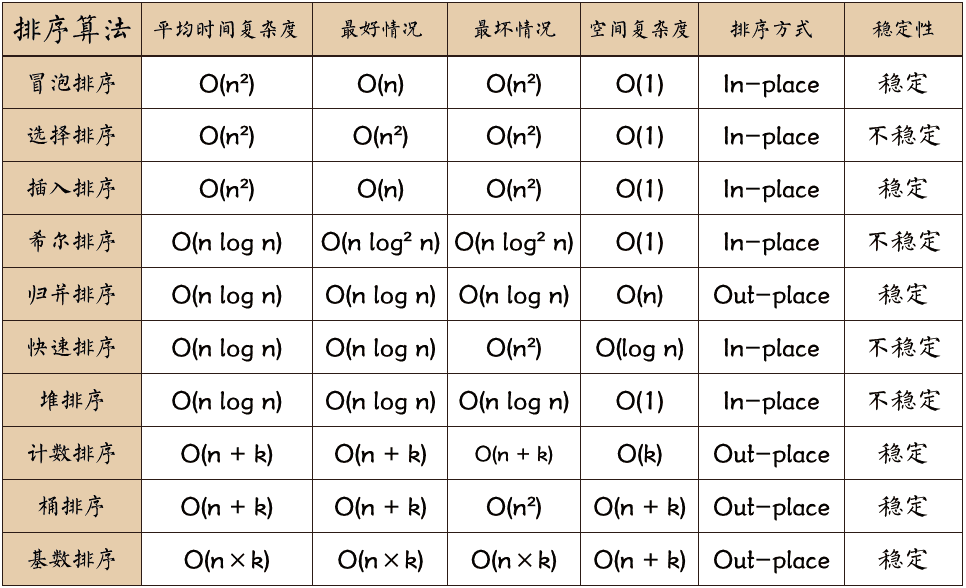
# 1. 堆排序概述**

堆排序是一种基于堆数据结构的排序算法。它将输入数组转换为一个最大堆，然后依次从堆中提取最大元素，从而实现排序。堆排序具有时间复杂度为 O(n log n) 的效率，并且在实际应用中具有较好的性能。

# 2. 堆排序理论基础

### 2.1 堆数据结构

**定义：**
堆是一种完全二叉树数据结构，其中每个节点的值都大于或等于其子节点的值。

**特性：**
- **完全二叉树：**除了最后一层，所有层都完全填充。
- **最大堆：**每个节点的值都大于或等于其子节点的值。
- **最小堆：**每个节点的值都小于或等于其子节点的值。

### 2.2 堆排序算法原理

堆排序是一种基于堆数据结构的排序算法。其基本原理如下：

**步骤：**

1. **构建堆：**将输入数组转换为最大堆。
2. **交换根节点：**将最大堆的根节点与最后一个元素交换。
3. **重建堆：**将剩余的堆重新构建为最大堆。
4. **重复步骤 2 和 3：**重复步骤 2 和 3，直到堆中只剩下一个元素。

**代码示例：**

def heap_sort(arr):
    # 构建最大堆
    build_max_heap(arr)

    # 循环交换根节点和最后一个元素
    for i in range(len(arr) - 1, 0, -1):
        # 交换根节点和最后一个元素
        arr[0], arr[i] = arr[i], arr[0]

        # 重建堆
        max_heapify(arr, 0, i)

# 构建最大堆
def build_max_heap(arr):
    for i in range(len(arr) // 2 - 1, -1, -1):
        max_heapify(arr, i, len(arr))

# 重建堆
def max_heapify(arr, i, n):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    # 找到最大值
    if left < n and arr[left] > arr[largest]:
        largest = left

    if right < n and arr[right] > arr[largest]:
        largest = right

    # 交换最大值和根节点
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]

        # 递归重建堆
        max_heapify(arr, largest, n)

**逻辑分析：**

- `build_max_heap` 函数将输入数组转换为最大堆。
- `max_heapify` 函数重建堆，确保每个节点的值都大于或等于其子节点的值。
- `heap_sort` 函数通过循环交换根节点和最后一个元素，并将剩余的堆重建为最大堆，最终完成排序。

# 3.1 堆排序实现步骤

堆排序的实现步骤可以分为以下几个部分：

1. **构建最大堆：**将输入数组中的元素构建成一个最大堆。最大堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。
2. **交换根节点和最后一个元素：**将最大堆的根节点（最大值）与最后一个元素交换。
3. **重新调整堆：**将交换后的最后一个元素重新调整为最大堆，确保满足最大堆的性质。
4. **重复步骤 2 和 3：**重复步骤 2 和 3，直到堆中只剩下一个元素。

**代码实现：**

def heap_sort(arr):
    """
    堆排序算法

    参数：
        arr：待排序的数组

    返回：
        排序后的数组
    """

    # 构建最大堆
    build_max_heap(arr)

    # 逐个交换根节点和最后一个元素，并重新调整堆
    for i in range(len(arr) - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        max_heapify(arr, 0, i)

    return arr


def build_max_heap(arr):
    """
    构建最大堆

    参数：
        arr：待构建最大堆的数组
    """

    # 从最后一个非叶节点开始，逐个向下调整堆
    for i in range(len(arr) // 2 - 1, -1, -1):
        max_heapify(arr, i, len(arr))


def max_heapify(arr, i, heap_size):
    """
    重新调整堆，确保满足最大堆性质

    参数：
        arr：待调整的数组
        i：当前节点的索引
        heap_size：堆的大小
    """

    # 左子节点的索引
    left = 2 * i + 1
    # 右子节点的索引
    right = 2 * i + 2

    # 找出左右子节点中较大的节点
    largest = i
    if left < heap_size and arr[left] > arr[largest]:
        largest = left
    if right < heap_size and arr[right] > arr[largest]:
        largest = right

    # 如果当前节点不是最大节点，交换当前节点和最大节点，并继续调整
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        max_heapify(arr, largest, heap_size)

### 3.2 时间复杂度分析

堆排序的时间复杂度主要取决于构建最大堆和重新调整堆的次数。

**构建最大堆：**构建最大堆的时间复杂度为 O(n)，其中 n 是数组的长度。这是因为构建最大堆需要对每个元素进行一次调整，而调整操作的时间复杂度为 O(log n)。

**重新调整堆：**重新调整堆的时间复杂度为 O(n log n)。这是因为在重新调整堆的过程中，需要对每个元素进行 log n 次调整操作，而调整操作的时间复杂度为 O(log n)。

因此，堆排序的总时间复杂度为 O(n log n)。

# 4. 堆排序优化技巧

### 4.1 堆的优化策略

**1. 数组表示堆**

传统上，堆是使用二叉树结构表示的。但是，为了提高内存利用率和访问效率，可以采用数组来表示堆。数组表示的堆中，根节点位于数组的第一个元素，其左子节点位于 2 * i，右子节点位于 2 * i + 1，其中 i 为父节点在数组中的索引。

**2. 二叉堆的平衡性**

堆的平衡性是指堆中各子树的高度相近。平衡的堆可以减少排序过程中的比较次数，从而提高排序效率。可以通过旋转操作来维护堆的平衡性。

**3. 懒惰删除**

在堆排序中，删除堆顶元素后，需要重新调整堆的结构。为了提高效率，可以采用懒惰删除策略。即在删除堆顶元素后，不立即调整堆的结构，而是将该元素标记为已删除。在后续操作中，当需要访问该元素时，再进行调整。

### 4.2 算法性能提升方法

**1. 使用小顶堆**

在堆排序中，通常使用大顶堆，即堆顶元素是堆中最大的元素。但是，对于某些应用场景，使用小顶堆（堆顶元素是最小元素）可以提高排序效率。

**2. 分治排序**

堆排序可以与分治排序相结合，以提高大规模数据的排序效率。分治排序将数据分为较小的子集，分别对子集进行堆排序，然后再合并子集的排序结果。

**3. 多线程优化**

对于多核处理器系统，可以采用多线程优化技术来提升堆排序的性能。将数据分为多个子集，并使用多个线程同时对子集进行堆排序，可以有效利用多核处理器的计算能力。

**4. 归并排序优化**

堆排序和归并排序都是稳定的排序算法。将堆排序与归并排序相结合，可以利用堆排序的快速排序能力和归并排序的稳定性，获得更好的排序效果。

**代码示例：**

# 数组表示的堆
class Heap:
    def __init__(self, arr):
        self.arr = arr
        self.size = len(arr)

    # 获取左子节点索引
    def left(self, i):
        return 2 * i + 1

    # 获取右子节点索引
    def right(self, i):
        return 2 * i + 2

    # 调整堆的平衡性
    def heapify(self, i):
        left = self.left(i)
        right = self.right(i)
        largest = i
        if left < self.size and self.arr[left] > self.arr[largest]:
            largest = left
        if right < self.size and self.arr[right] > self.arr[largest]:
            largest = right
        if largest != i:
            self.arr[i], self.arr[largest] = self.arr[largest], self.arr[i]
            self.heapify(largest)

# 堆排序
def heap_sort(arr):
    heap = Heap(arr)
    for i in range(heap.size // 2 - 1, -1, -1):
        heap.heapify(i)
    for i in range(heap.size - 1, 0, -1):
        heap.arr[0], heap.arr[i] = heap.arr[i], heap.arr[0]
        heap.size -= 1
        heap.heapify(0)

**逻辑分析：**

该代码实现了数组表示的堆排序算法。

* `heapify` 函数用于调整堆的平衡性，确保堆满足大顶堆的性质。
* `heap_sort` 函数执行堆排序算法，将数组中的元素从小到大排序。

**参数说明：**

* `arr`：需要排序的数组

# 5. 堆排序应用场景

### 5.1 堆排序在数据结构中的应用

堆排序在数据结构中有着广泛的应用，主要体现在以下几个方面：

- **优先队列实现：**堆是一种天然的优先队列数据结构，可以高效地实现优先级队列的各种操作，如插入、删除和查询最小/最大元素。

- **中位数维护：**通过维护一个最大堆和一个最小堆，可以快速地维护一个集合的中位数。

- **堆树：**堆排序算法可以用来构造堆树，这是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。堆树在各种算法中都有应用，如哈夫曼编码和 Dijkstra 算法。

### 5.2 堆排序在算法竞赛中的应用

堆排序在算法竞赛中也是一种常用的排序算法，主要用于解决以下类型的问题：

- **k 个最大/最小元素：**给定一个数组，快速找到其中的 k 个最大或最小元素。

- **逆序对：**给定一个数组，计算其中逆序对的个数。逆序对是指两个元素 i 和 j，其中 i < j 但 arr[i] > arr[j]。

- **范围查询：**给定一个数组和一个范围 [l, r]，快速找到该范围内的最大或最小元素。

**代码示例：**

# 使用堆排序查找数组中的 k 个最大元素

import heapq

def find_k_largest(arr, k):
    # 创建一个最大堆
    heapq.heapify(arr)

    # 弹出堆顶 k 次，得到 k 个最大元素
    result = []
    for _ in range(k):
        result.append(heapq.heappop(arr))

    return result

**逻辑分析：**

该代码使用 Python 的 `heapq` 模块来实现堆排序。首先，将输入数组 `arr` 转换为一个最大堆。然后，依次弹出堆顶元素 k 次，得到 k 个最大元素。

**参数说明：**

* `arr`：输入数组
* `k`：要查找的最大元素个数

# 6.1 堆排序与快速排序比较

堆排序和快速排序都是经典的排序算法，各有其优缺点。

**时间复杂度：**
- 堆排序：平均时间复杂度为 O(n log n)，最坏时间复杂度也为 O(n log n)。
- 快速排序：平均时间复杂度为 O(n log n)，最坏时间复杂度为 O(n^2)。

**空间复杂度：**
- 堆排序：原地排序，空间复杂度为 O(1)。
- 快速排序：需要额外的空间存储递归栈，空间复杂度为 O(log n)。

**稳定性：**
- 堆排序：不稳定，即相同元素在排序后的顺序可能发生变化。
- 快速排序：稳定，即相同元素在排序后的顺序保持不变。

**平均性能：**
- 堆排序：在大多数情况下，堆排序的性能都优于快速排序。
- 快速排序：当数组元素分布接近有序时，快速排序的性能会更好。

**最坏情况：**
- 堆排序：堆排序的最坏情况发生在数组完全逆序时。
- 快速排序：快速排序的最坏情况发生在数组元素分布接近有序时。

**代码示例：**

# 堆排序
def heap_sort(arr):
    # 构建最大堆
    for i in range(len(arr) // 2 - 1, -1, -1):
        heapify(arr, i, len(arr))

    # 依次弹出堆顶元素
    for i in range(len(arr) - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, 0, i)

# 快速排序
def quick_sort(arr):
    if len(arr) <= 1:
        return

    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]

    quick_sort(left)
    quick_sort(right)

    arr[:] = left + middle + right

**总结：**
堆排序和快速排序都是高效的排序算法，各有其优缺点。堆排序在平均情况下性能更优，而快速排序在最坏情况下性能更优。在实际应用中，需要根据具体场景选择合适的排序算法。