堆排序实战应用场景：探索堆排序在实际中的价值，解决排序难题

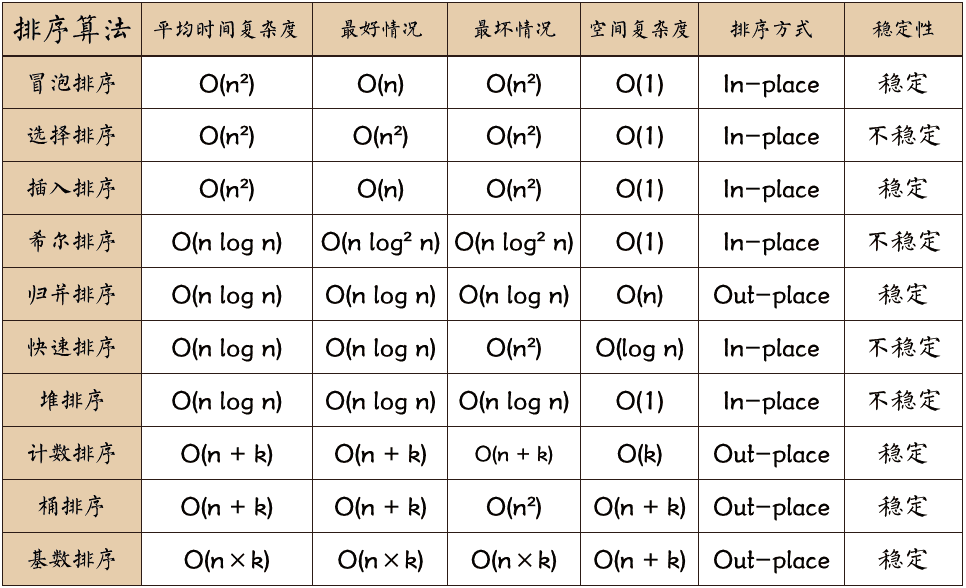
# 1. 堆排序算法原理及实现

堆排序是一种基于堆数据结构的排序算法。它将输入数据构建成一个最大堆，然后依次弹出堆顶元素，即可得到有序序列。

实现堆排序算法需要以下步骤：

1. **构建最大堆：**将输入数据按照最大堆的性质进行调整，即每个节点的值都大于或等于其子节点的值。
2. **弹出堆顶元素：**将堆顶元素（最大值）弹出，并将其放入有序序列中。
3. **调整堆：**将堆顶元素的子节点重新调整为最大堆，并重复步骤 2 和 3，直到堆为空。

# 2. 堆排序算法的性能分析

### 2.1 时间复杂度和空间复杂度

堆排序算法的时间复杂度主要取决于堆的构建和排序过程。

**堆的构建：**
堆的构建需要将无序数组转换为一个最大堆。对于包含 n 个元素的数组，堆的构建时间复杂度为 O(n log n)。

**排序过程：**
排序过程从最大堆中依次取出最大元素，并将其放置在数组的末尾。每取出一个元素，需要重新调整堆的结构以保持最大堆性质。对于包含 n 个元素的数组，排序过程的时间复杂度为 O(n log n)。

因此，堆排序算法的总时间复杂度为 O(n log n)。

堆排序算法的空间复杂度为 O(1)，因为它不需要额外的空间来存储临时数据。

### 2.2 与其他排序算法的比较

| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 堆排序 | O(n log n) | O(1) | 不稳定 |
| 归并排序 | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(log n) | 不稳定 |
| 冒泡排序 | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(1) | 不稳定 |

从表格中可以看出，堆排序算法的时间复杂度与归并排序和快速排序相同，均为 O(n log n)。然而，堆排序算法的空间复杂度为 O(1)，而归并排序和快速排序的空间复杂度分别为 O(n) 和 O(log n)。因此，在需要最小空间复杂度的场景中，堆排序算法是一个不错的选择。

此外，堆排序算法是不稳定的，这意味着它不会保持相等元素的相对顺序。而归并排序算法是稳定的，它会保持相等元素的相对顺序。

# 3.1 数据挖掘和机器学习

堆排序算法在数据挖掘和机器学习领域有着广泛的应用。在这些领域中，数据量通常很大，需要高效的排序算法来处理。堆排序算法的平均时间复杂度为 O(n log n)，这使其非常适合处理大型数据集。

**在数据挖掘中，堆排序算法可用于：**

- 对数据进行预处理，例如排序和分组
- 发现数据中的模式和趋势
- 构建分类和回归模型

**在机器学习中，堆排序算法可用于：**

- 对训练数据进行排序，以提高模型的性能
- 构建决策树和支持向量机等分类模型
- 训练神经网络，其中需要对数据进行排序以进行反向传播

### 3.2 大数据处理

在处理大数据时，堆排序算法也是一个有价值的工具。大数据数据集通常包含数十亿甚至数万亿个数据点，需要高效的排序算法才能在合理的时间内处理。堆排序算法的平均时间复杂度为 O(n log n)，这使其非常适合处理大型数据集。

**在处理大数据时，堆排序算法可用于：**

- 对数据进行排序，以进行分析和可视化
- 查找数据中的异常值和异常情况
- 构建大规模机器学习模型

### 3.3 排序算法竞赛

堆排序算法也是排序算法竞赛中常用的算法。在这些竞赛中，参与者必须在给定的时间限制内对数据集进行排序。堆排序算法的平均时间复杂度为 O(n log n)，