【进阶篇】MATLAB中的图像修复:使用稀疏表示进行图像修复
发布时间: 2024-05-21 18:07:07 阅读量: 88 订阅数: 236 


基于稀疏表示(mp算法)的图像修复算法(含Matlab源码)
1、实现效果:《【毕业设计/Matlab系列】基于稀疏表示(mp算法)的图像修复》见链接:https://blog.csdn.net/SoaringLee_fighting/article/details/124415648 2、内容介绍:基于稀疏表示(mp算法)的图像修复matlab实现,效果很好。 3、适用人群:适用于计算机,电子信息工程等专业的大学生课程设计和毕业设计。 4、支持答疑:有问题可以订阅博主的《实用毕业设计》专栏(附链接 :https://blog.csdn.net/soaringlee_fighting/category_9288245.html)或者直接购买资源后咨询博主。 5、质量保证:完整代码,可直接运行!资源里面包含使用说明文档。
# 1. 图像修复概述**
图像修复是一项计算机视觉技术,旨在修复损坏或退化的图像,使其恢复到原始状态。图像损坏的原因可能是噪声、划痕、丢失像素或其他失真。图像修复算法通过分析图像的局部特征和纹理,重构缺失或损坏的区域,从而恢复图像的完整性。
图像修复在各个领域都有广泛的应用,例如:
* **文物修复:**修复历史图像或文物中的损坏和失真。
* **医学成像:**增强医学图像的质量,提高诊断的准确性。
* **计算机视觉:**提高图像识别和对象检测算法的性能。
* **图像编辑:**移除图像中的瑕疵和不需要的元素,增强图像的视觉效果。
# 2. 稀疏表示理论
### 2.1 稀疏表示的基本原理
稀疏表示理论是一种数学框架,用于将信号或数据表示为仅包含少量非零元素的稀疏向量。它基于这样一个假设:许多自然信号和数据具有内在的稀疏性,这意味着它们可以用少量非零元素来准确表示。
稀疏表示的数学模型如下:
```
x = Φα
```
其中:
* **x** 是原始信号或数据,是一个 n 维向量
* **Φ** 是一个 m × n 的字典矩阵,包含一组基向量
* **α** 是一个 m 维稀疏向量,仅包含少量非零元素
字典矩阵 **Φ** 中的基向量是精心设计的,以捕捉原始信号或数据中的特征。通过求解稀疏向量 **α**,我们可以将原始信号或数据表示为字典中基向量的线性组合。
### 2.2 稀疏表示的算法和优化
求解稀疏向量 **α** 是一个优化问题,目标是找到一个稀疏解,使重构信号 **x** 与原始信号尽可能接近。常用的稀疏表示算法包括:
* **正交匹配追踪 (OMP)**:一种贪婪算法,逐个添加基向量,直到重构信号达到预定义的精度。
* **最小角回归 (LARS)**:一种迭代算法,通过最小化重构信号和原始信号之间的残差来更新稀疏向量。
* **基追踪 (BP)**:一种基于贝叶斯框架的算法,使用概率模型来估计稀疏向量。
这些算法通常需要解决以下优化问题:
```
min ||x - Φα||_2^2 + λ||α||_0
```
其中:
* **||x - Φα||_2^2** 是重构信号和原始信号之间的均方误差
* **||α||_0** 是稀疏向量的非零元素个数
* **λ** 是正则化参数,用于控制稀疏性
该优化问题可以通过各种方法求解,例如凸优化、贪婪算法和贝叶斯
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
0
0
相关推荐
SW_孙维
开发技术专家
知名科技公司工程师,开发技术领域拥有丰富的工作经验和专业知识。曾负责设计和开发多个复杂的软件系统,涉及到大规模数据处理、分布式系统和高性能计算等方面。
专栏简介
MATLAB图像处理合集专栏提供了一系列全面且深入的教程,涵盖了图像处理的各个方面。从基础概念,如图像绘制、读取和格式转换,到高级技术,如图像融合、去噪和特征提取。专栏还包括实战演练,展示了图像处理在实际应用中的应用,例如人脸检测、图像去雾和车牌识别。无论是初学者还是经验丰富的图像处理人员,这个专栏都提供了宝贵的资源,帮助他们掌握MATLAB图像处理的强大功能。
专栏目录
最低0.47元/天 解锁专栏
买1年送3月
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
最新推荐
【AUTOSAR集成秘笈】:调试、诊断与测试,全面掌握Vector工具链
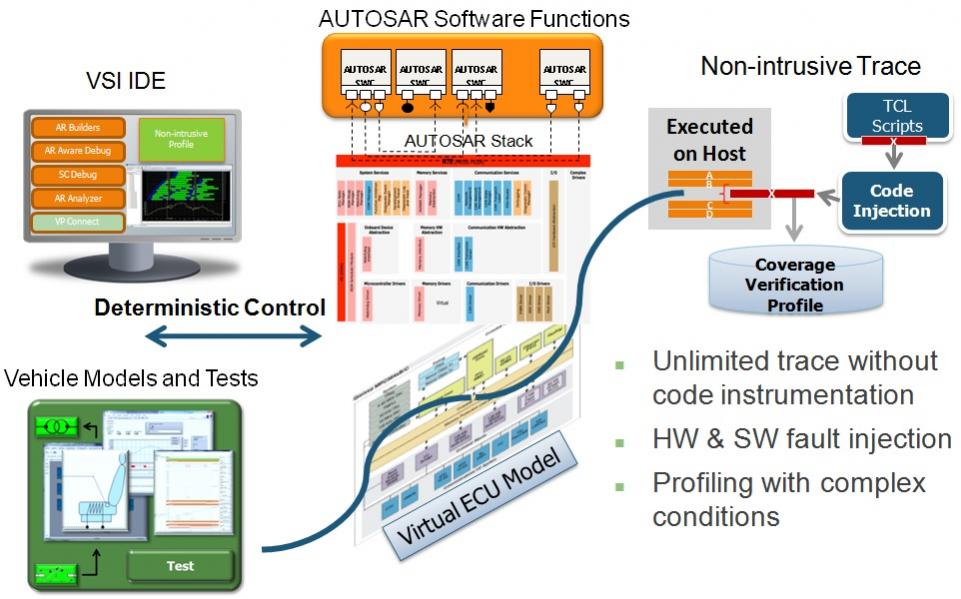
# 摘要
本文详细探讨了AUTOSAR集成的基础知识与Vector工具链的实际应用。首先概述了AUTOSAR标准的历史演变与基础架构,重点分析了模块化原理和集成方法论。接着,深入介绍了Vector工具链在调试、诊断、测试和验证中的应用,提供了详细的实践案例和故障处理策略。此外,文章还探讨了Vector工具链在多ECU系统集成、高级诊断功能开发以及持续集成与持续部署(CI/C
【数据库查询优化】:网上购物系统的用户体验革命
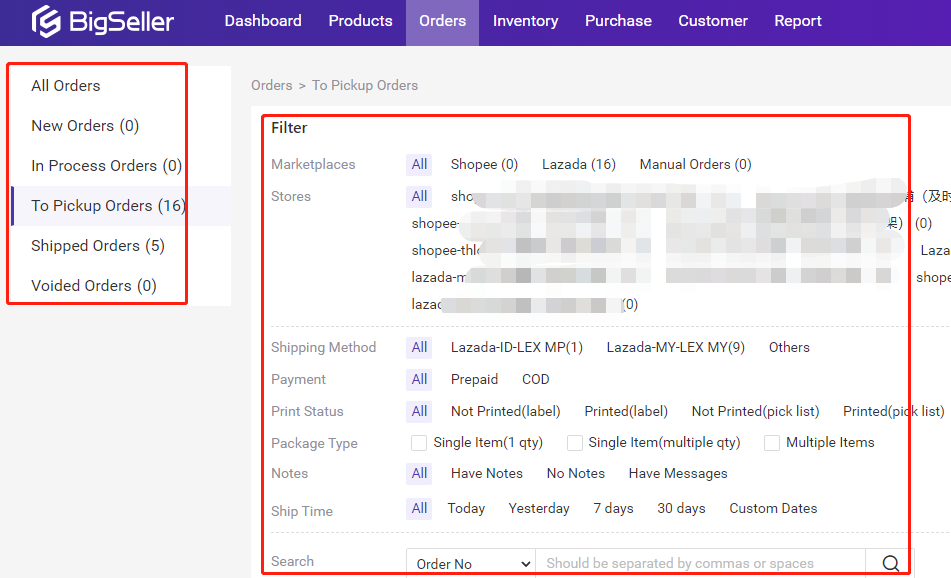
# 摘要
数据库查询优化是确保系统性能和效率的关键环节。本文系统阐述了数据库查询优化的重要性,介绍了性能分析基础、SQL查询优化理论,并探讨了优化策略与最佳实践。此外,本文还分析了数据库设计中的规范化与反规范化,索引优化技术以及查询重写的技巧。通过性能监控工具的介绍和案例分析,本文进一步展示了优化技术在实际应用中的效果。最后,以网上购物系统为例,本文探讨了查询优化如何提高用户体验,评估了优化措施的实际成效。本文旨在为数据库开发者
【移动安全与KNOX】:确保设备应用安全的策略与技巧
# 摘要
随着移动设备使用量的快速增长,移动安全问题日益凸显,安全威胁多样化,对企业和个人用户构成了潜在风险。本文首先概述移动安全的必要性和当前面临的主要威胁,随后介绍KNOX平台的架构、安全核心组件和关键特性,包括企业级安全管理、数据保护与加密以及应用程序安全框架。文中进一步探讨了KNOX安全策略的实施细节,如策略配置、用户身份验证和授权等,并针对移动应用的安全开发与管理提出标准化实践。最后,通过分享KNOX的实战案例与技巧,提供部署和安全管理的洞见,并讨论针对新型威胁的策略调整。
# 关键字
移动安全;KNOX平台;安全策略实施;安全开发管理;数据加密;安全威胁
参考资源链接:[突破三
【十进制调整必要性】:DAS指令在汇编语言中的角色解析

# 摘要
DAS指令作为汇编语言中用于十进制调整的关键指令,对于处理数字数据及转换计算尤为重要。本文首先概述了DAS指令的基本概念和汇编语言基础,随后深入探讨了DAS指令的理论基础,包括十进制与二进制的转换机制及其必要性,以及DAS指令在现代处理器指令集中的功能和位置。通过编程实践章节,本文展示了如何搭建汇编环境、研究指令集,并示范了DAS指令的基本使用
工程仿真数据整合术:TECPLOT高效操作秘籍

# 摘要
本文全面介绍了TECPLOT软件的功能及其在工程仿真中的应用。首先,概述了TECPLOT的基本概念和安装步骤,为用户搭建起使用该软件的基础框架。随后,详细阐述了TECPLOT的基础操作,包括用户界面布局、数据导入、表格管理和变量处理,为进行有效数据可视化打下坚实基础。第三章深入探讨了绘图技术,涵盖了图形绘制、视觉效果提升以及高级操作和样式
【开关电源设计秘籍】:掌握峰值电流模式的7大实战技巧

# 摘要
峰值电流模式作为开关电源控制策略的一种,因其高精度和稳定性在电源管理领域得到广泛应用。本文深入探讨了峰值电流模式的基本概念、理论基础及其工作原理,包括电流感测技术、控制芯片选择与应用等
【CVX与MATLAB混合编程艺术】:整合CVX在工程中的应用技巧

# 摘要
本文全面介绍了CVX与MATLAB混合编程的技术细节和应用实践,旨在帮助研究者和工程师有效地解决优化问题。首先概述了混合编程的基础概念和理论,随后深入探讨了CVX在凸优化问题中的数学建模和求解器选择,以及MATLAB接口的使用和模型构建技巧。接着,分析了CVX在信号处理、金融工程和控制系统设计等多个领域内的具体应用案例
GN25L95-Semtech芯片:生产测试与质量控制的完整流程

# 摘要
本文详细介绍了GN25L95-Semtech芯片的测试与质量控制流程,深入探讨了生产测试的理论基础,包括半导体器件的测试原理、步骤与方法论,以及测试设备与工具的应用。此外,本文还阐述了质量控制体系的构建、持续改进和风险管理策略,以及测试与控制的高级技术。最后,文章展望了未来测试与质量控制的趋势,特别是人工智能技术的应用、可持续性对产业的影响以及行业标准的演变,为提升半导体产业的测试效率和产品质量提供了
【x64dbg注入技术:DLL注入与执行流程实战】
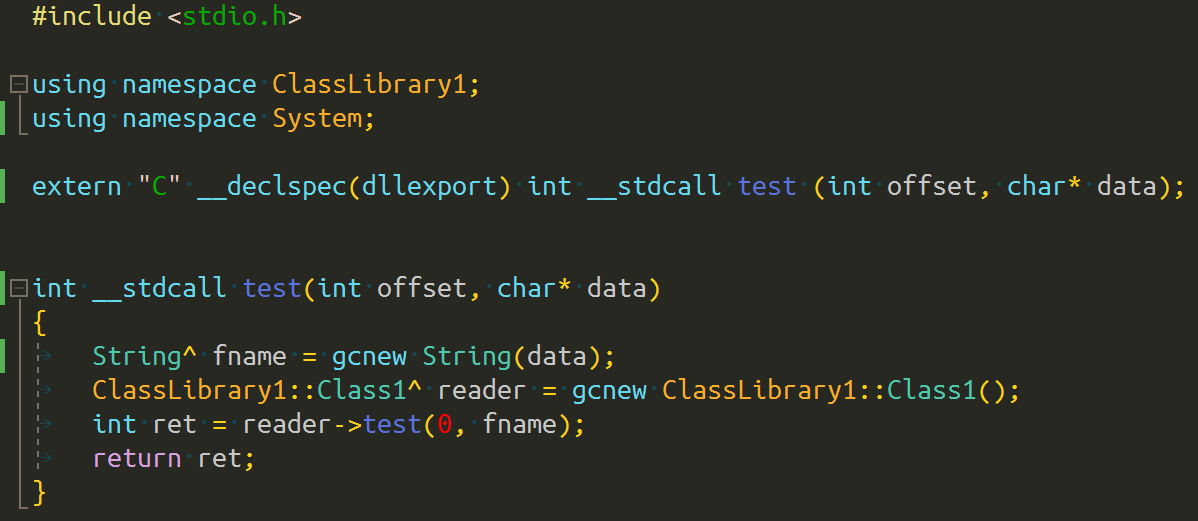
# 摘要
本文深入探讨了x64dbg注入技术的理论与实践,从DLL注入的基础理论到高级技术实现,系统地分析了DLL注入的目的、原理及关键概念。文章详细介绍了DLL注入的主要方法,如API挂钩、CreateRemoteThread和SetWindowsHookEx,并进一步指导如何利用x64dbg工具和手动操作进行DLL注入。深入分析了注入后的执行流程、稳定性和安全性问题,以
【金融模型专家】:从理论到实践,彻底掌握随机过程在金融市场中的应用

# 摘要
随机过程理论为金融市场分析提供了强有力的数学工具,它在定价模型、风险管理和量化策略开发中扮演着核心角色。本文首先回顾了随机过程的理论基础及其在金融市场中的基本应用,然后深入探讨了模拟方法、VaR计算和动量与反转策略等实践应用。高级技术章节着重于GARCH模型、高频交易和机器学习技术的结合,最后通过案例研究分析展示了如何应用随机过程进行市场数据分析、交易策略的开发测试以
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



专栏目录
最低0.47元/天 解锁专栏
买1年送3月
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
