揭秘多层感知器（MLP）：架构、原理和应用，打造高效神经网络

# 1. 多层感知器（MLP）概述

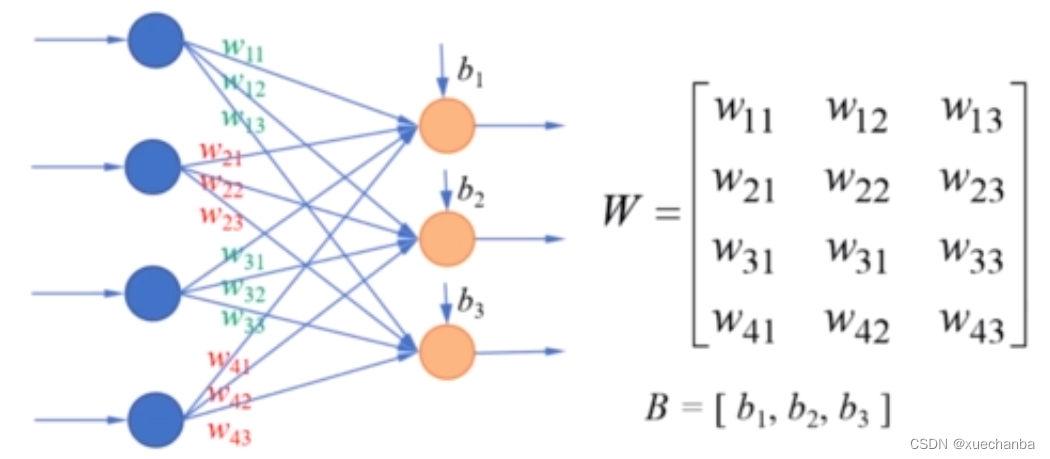
多层感知器（MLP）是一种前馈神经网络，由多层感知器组成，每层感知器都将前一层的输出作为输入。MLP 的结构简单，易于训练，在图像分类、自然语言处理和金融预测等领域有着广泛的应用。

MLP 的基本结构包括输入层、隐藏层和输出层。输入层接收输入数据，隐藏层对输入数据进行非线性变换，输出层输出最终结果。MLP 的前向传播过程从输入层开始，逐层计算，直至输出层。反向传播过程则从输出层开始，逐层计算梯度，直至输入层。

MLP 的激活函数和损失函数是影响其性能的关键因素。常用的激活函数包括 sigmoid、tanh 和 ReLU，而常用的损失函数包括交叉熵损失和均方误差损失。

# 2. MLP的架构与原理

### 2.1 MLP的基本结构

多层感知器（MLP）是一种前馈神经网络，由多个全连接层堆叠而成。其基本结构如下图所示：

graph LR
subgraph 输入层
    A[x1]
    B[x2]
    C[x3]
end
subgraph 隐藏层1
    D[h1]
    E[h2]
    F[h3]
end
subgraph 隐藏层2
    G[h4]
    H[h5]
    I[h6]
end
subgraph 输出层
    J[y]
end
A-->D
B-->D
C-->D
D-->G
E-->G
F-->G
G-->J
H-->J
I-->J

MLP的每一层由神经元组成，神经元接收上一层输出的加权和，并通过激活函数生成输出。

### 2.2 MLP的前向传播和反向传播

**前向传播**

前向传播是MLP计算输出的过程。对于输入向量 `x = [x1, x2, ..., xn]`，MLP的计算过程如下：

1. **隐藏层计算：**
- 计算隐藏层 `l` 的激活值 `h_l`：

     h_l = σ(W_l * x + b_l)

- 其中，`W_l` 是权重矩阵，`b_l` 是偏置向量，`σ` 是激活函数。

2. **输出层计算：**
- 计算输出层激活值 `y`：

     y = σ(W_out * h_L + b_out)

- 其中，`W_out` 是输出层权重矩阵，`b_out` 是输出层偏置向量。

**反向传播**

反向传播是MLP训练的过程。它通过计算损失函数的梯度来更新权重和偏置。

1. **计算误差：**
- 计算输出层误差 `δ_out`：

     δ_out = (y - t) * σ'(W_out * h_L + b_out)

- 其中，`t` 是真实标签，`σ'` 是激活函数的导数。

2. **计算隐藏层误差：**
- 计算隐藏层 `l` 的误差 `δ_l`：

     δ_l = (W_{l+1}^T * δ_{l+1}) * σ'(W_l * x + b_l)

3. **更新权重和偏置：**
- 更新权重矩阵 `W_l`：

     W_l = W_l - α * δ_l * x^T

- 更新偏置向量 `b_l`：

     b_l = b_l - α * δ_l

- 其中，`α` 是学习率。

### 2.3 MLP的激活函数和损失函数

**激活函数**

MLP中常用的激活函数包括：

- sigmoid：`σ(x) = 1 / (1 + e^(-x))`
- tanh：`σ(x) = (e^x - e^(-x)) / (e^x + e^(-x))`
- ReLU：`σ(x) = max(0, x)`

**损失函数**

MLP中常用的损失函数包括：

- 平方损失：`L(y, t) = (y - t)^2`
- 交叉熵损失：`L(y, t) = -t * log(y) - (1 - t) * log(1 - y)`

# 3. MLP的训练与优化

### 3.1 MLP的训练算法

MLP的训练过程是一个迭代优化过程，目的是找到一组最优的权重和偏置，使得MLP模型能够在给定的数据集上达到最小的损失函数值。常用的MLP训练算法包括：

- **梯度下降算法：**梯度下降算法通过迭代地更新权重和偏置，使损失函数值逐渐减小。在每次迭代中，算法计算损失函数关于权重和偏置的梯度，并沿梯度负方向更新权重和偏置。
- **动量法：**动量法在梯度下降算法的基础上，加入了动量项，可以加速收敛速度。动量项记录了权重和偏置的更新历史，并将其与当前的梯度结合，用于更新权重和偏置。
- **RMSprop算法：**RMSprop算法是一种自适应学习率的梯度下降算法。它通过计算梯度的均方根（RMS）来动态调整学习率，可以有效防止过拟合。
- **Adam算法：**Adam算法是RMSprop算法和动量法的结合，它既具有自适应学习率的优点，又可以加速收敛速度。

### 3.2 MLP的超参数调优

MLP的超参数包括学习率、批量大小、激活函数、正则化参数等。超参数调优的目标是找到一组最优的超参数，使得MLP模型在验证集上达到最佳的性能。常用的超参数调优方法包括：

- **网格搜索：**网格搜索是一种穷举搜索的方法，它遍历给定的超参数取值范围，并选择使验证集损失函数值最小的超参数组合。
- **随机搜索：**随机搜索是一种基于概率的方法，它随机抽取超参数组合，并选择使验证集损失函数值最小的超参数组合。
- **贝叶斯优化：**贝叶斯优化是一种基于贝叶斯定理的方法，它通过构建超参数空间的概率模型，指导超参数的搜索过程。

### 3.3 MLP的正则化技术

正则化技术可以防止MLP模型过拟合，提高模型的泛化能力。常用的正则化技术包括：

- **L1正则化：**L1正则化在损失函数中加入权重和偏置的L1范数，可以使权重和偏置稀疏化，从而防止过拟合。
- **L2正则化：**L2正则化在损失函数中加入权重和偏置的L2范数，可以使权重和偏置平滑化，从而防止过拟合。
- **Dropout：**Dropout是一种随机失活技术，它在训练过程中随机失活一部分神经元，可以防止神经元之间过度拟合。
- **数据增强：**数据增强是一种通过对训练数据进行变换（如旋转、裁剪、翻转等）来增加训练数据量的方法，可以防止模型过拟合。

# 4. MLP的应用实践

### 4.1 MLP在图像分类中的应用

MLP在图像分类任务中表现出色，其强大的特征提取能力使其能够从图像中学习复杂的模式。

**应用场景：**

* 物体检测
* 图像识别
* 图像分割

**具体实现：**

1. **数据预处理：**将图像转换为固定大小的数组，并进行归一化处理。
2. **MLP模型构建：**根据图像特征和分类类别，设计MLP网络结构，包括输入层、隐含层和输出层。
3. **训练模型：**使用训练数据集训练MLP模型，调整权重和偏差以最小化损失函数。
4. **评估模型：**使用验证数据集评估模型的性能，包括准确率、召回率和F1分数。

### 4.2 MLP在自然语言处理中的应用

MLP在自然语言处理（NLP）任务中也得到广泛应用，其强大的文本表示能力使其能够理解文本的含义。

**应用场景：**

* 文本分类
* 情感分析
* 机器翻译

**具体实现：**

1. **文本预处理：**对文本进行分词、词性标注和向量化处理。
2. **MLP模型构建：**根据文本特征和分类类别，设计MLP网络结构，包括输入层、隐含层和输出层。
3. **训练模型：**使用训练数据集训练MLP模型，调整权重和偏差以最小化损失函数。
4. **评估模型：**使用验证数据集评估模型的性能，包括准确率、召回率和F1分数。

### 4.3 MLP在金融预测中的应用

MLP在金融预测任务中也发挥着重要作用，其非线性拟合能力使其能够捕捉金融数据的复杂变化。

**应用场景：**

* 股票价格预测
* 外汇汇率预测
* 经济指标预测

**具体实现：**

1. **数据收集：**收集历史金融数据，包括价格、成交量、经济指标等。
2. **特征工程：**提取和处理金融数据的相关特征，如移动平均线、相对强弱指数（RSI）等。
3. **MLP模型构建：**根据金融数据特征和预测目标，设计MLP网络结构，包括输入层、隐含层和输出层。
4. **训练模型：**使用训练数据集训练MLP模型，调整权重和偏差以最小化损失函数。
5. **评估模型：**使用验证数据集评估模型的性能，包括均方根误差（RMSE）、平均绝对误差（MAE）和最大绝对误差（MAE）。

# 5.1 卷积神经网络（CNN）

**简介**

卷积神经网络（CNN）是一种深度神经网络，专门设计用于处理具有网格状数据结构的输入，例如图像和视频。与 MLP 相比，CNN 具有以下主要优势：

* **局部连接性：**CNN 中的神经元只与输入数据的局部区域相连，这有助于提取局部特征。
* **权重共享：**CNN 中的卷积核在整个输入数据上共享权重，这减少了参数数量并促进了平移不变性。
* **池化层：**池化层通过对局部区域中的特征进行聚合，减少特征图的大小并增强鲁棒性。

**CNN 的架构**

CNN 的典型架构包括以下层：

* **卷积层：**卷积层应用卷积核提取输入数据的特征。
* **池化层：**池化层对卷积层的输出进行下采样，减少特征图的大小。
* **全连接层：**全连接层将卷积层的输出展平并连接到输出层。

**CNN 的训练**

CNN 的训练与 MLP 类似，但需要使用专门的优化器和损失函数。常用的优化器包括 Adam 和 RMSProp，而损失函数通常是交叉熵损失或均方误差损失。

**CNN 的应用**

CNN 在图像处理和计算机视觉领域有着广泛的应用，包括：

* 图像分类
* 目标检测
* 语义分割
* 图像生成

**示例**

以下代码示例展示了一个简单的 CNN 架构，用于图像分类：

import tensorflow as tf

# 定义输入数据
input_data = tf.keras.Input(shape=(28, 28, 1))

# 卷积层 1
conv1 = tf.keras.layers.Conv2D(32, (3, 3), activation='relu')(input_data)

# 池化层 1
pool1 = tf.keras.layers.MaxPooling2D((2, 2))(conv1)

# 卷积层 2
conv2 = tf.keras.layers.Conv2D(64, (3, 3), activation='relu')(pool1)

# 池化层 2
pool2 = tf.keras.layers.MaxPooling2D((2, 2))(conv2)

# 展平层
flatten = tf.keras.layers.Flatten()(pool2)

# 全连接层
dense1 = tf.keras.layers.Dense(128, activation='relu')(flatten)

# 输出层
output = tf.keras.layers.Dense(10, activation='softmax')(dense1)

# 定义模型
model = tf.keras.Model(input_data, output)

# 编译模型
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10)

**逻辑分析**

此代码示例定义了一个包含两个卷积层、两个池化层和两个全连接层的 CNN 模型。卷积层提取输入图像的特征，而池化层减少特征图的大小并增强鲁棒性。全连接层将卷积层的输出展平并连接到输出层，输出层使用 softmax 激活函数进行多类分类。

# 6.1 MLP在边缘计算中的应用

随着物联网（IoT）设备和边缘计算的兴起，MLP在边缘计算中的应用越来越受到关注。边缘计算是一种分布式计算范式，它将计算和存储资源部署在靠近数据源的位置，从而减少延迟和提高效率。

MLP在边缘计算中具有以下优势：

- **低延迟：** MLP的计算复杂度相对较低，可以在边缘设备上快速执行，从而实现低延迟的实时决策。
- **低功耗：** MLP的模型规模通常较小，所需计算资源较少，这使其非常适合在功耗受限的边缘设备上部署。
- **适应性强：** MLP可以针对特定的边缘计算任务进行定制，例如图像分类、异常检测和预测。

在边缘计算中，MLP可以用于以下应用：

- **工业物联网（IIoT）：** MLP可以用于监测工业设备，检测异常并预测维护需求。
- **智能家居：** MLP可以用于控制智能家居设备，例如灯光、恒温器和安全系统。
- **自动驾驶：** MLP可以用于处理传感器数据，实时做出决策，例如物体检测和路径规划。

## 6.2 MLP在人工智能中的创新应用

MLP在人工智能（AI）领域不断发展，并被用于各种创新应用中：

- **生成式对抗网络（GAN）：** MLP是GAN中的一个关键组件，用于生成逼真的数据或图像。
- **强化学习：** MLP可以作为价值函数或策略网络，用于指导强化学习代理的行为。
- **神经架构搜索（NAS）：** MLP可以用于自动设计和优化神经网络架构。
- **可解释人工智能（XAI）：** MLP可以用于解释复杂的神经网络模型的预测，提高其透明度和可信度。

随着AI技术的不断进步，MLP有望在未来发挥越来越重要的作用，为各种应用提供强大的学习和决策能力。