损失函数与多层感知器（MLP）：评估指标全解析，选择最优函数，提升模型准确性

# 1. 损失函数概述

损失函数是机器学习模型评估其预测结果与真实值之间差异的函数。它量化了模型在给定数据集上的准确性。常见的损失函数包括均方误差 (MSE)、平均绝对误差 (MAE) 和交叉熵损失。这些函数的理论基础和实践应用将在后续章节中详细讨论。

# 2. 多层感知器（MLP）中的损失函数

在多层感知器（MLP）中，损失函数衡量模型输出与真实标签之间的差异，是模型训练过程中优化目标的关键。本文将介绍 MLP 中常用的三种损失函数：均方误差 (MSE)、平均绝对误差 (MAE) 和交叉熵损失。

### 2.1 MSE（均方误差）

#### 2.1.1 理论基础

均方误差 (MSE) 是最常用的回归任务损失函数，它衡量预测值与真实值之间的平方差的平均值。其公式为：

MSE = (1/n) * ∑(y_i - y_hat_i)^2

其中：

* n 是样本数量
* y_i 是真实标签
* y_hat_i 是模型预测值

#### 2.1.2 实践应用

MSE 适用于预测连续值的目标变量，例如房价或温度。它对离群值敏感，因此当数据中存在极端值时，它可能会产生误导性的结果。

### 2.2 MAE（平均绝对误差）

#### 2.2.1 理论基础

平均绝对误差 (MAE) 是另一种回归任务损失函数，它衡量预测值与真实值之间的绝对差的平均值。其公式为：

MAE = (1/n) * ∑|y_i - y_hat_i|

其中：

* n 是样本数量
* y_i 是真实标签
* y_hat_i 是模型预测值

#### 2.2.2 实践应用

MAE 对离群值不敏感，因此当数据中存在极端值时，它比 MSE 更稳定。它适用于预测连续值的目标变量，例如客户流失率或销售额。

### 2.3 交叉熵损失

#### 2.3.1 理论基础

交叉熵损失是分类任务中常用的损失函数，它衡量预测概率分布与真实概率分布之间的差异。对于二分类问题，其公式为：

Cross-Entropy Loss = - (y_i * log(y_hat_i) + (1 - y_i) * log(1 - y_hat_i))

其中：

* y_i 是真实标签（0 或 1）
* y_hat_i 是模型预测的概率

#### 2.3.2 实践应用

交叉熵损失适用于预测离散值的目标变量，例如图像分类或文本分类。它对概率分布的差异敏感，因此当模型预测的概率与真实概率相差较大时，它会产生较大的损失值。

# 3. 损失函数评估指标

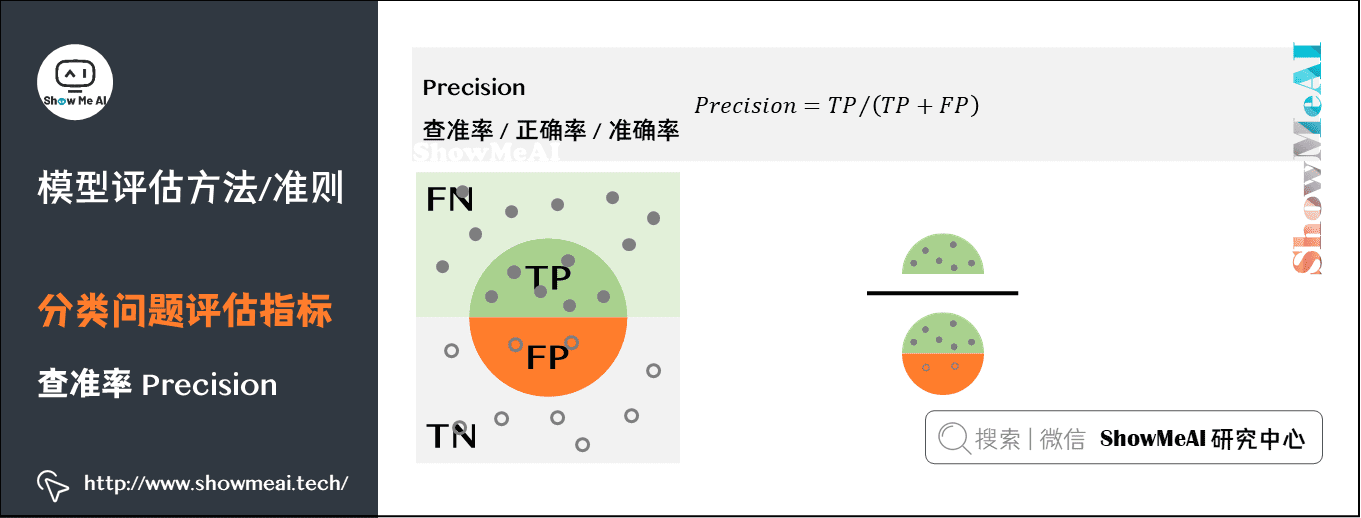
### 3.1 准确率

**3.1.1 定义和计算方法**

准确率是衡量分类模型性能的最基本指标，它表示模型对所有样本进行预测时，正确预测的比例。准确率的计算公式为：

准确率 = 正确预测样本数 / 总样本数

**3.1.2 优缺点**

* **优点：**简单易懂，计算方便。
* **缺点：**当样本分布不平衡时，准确率可能会失真。例如，如果一个数据集中有 90% 的正样本和 10% 的负样本，那么一个总是预测正样本的模型也会有 90% 的准确率，但这并不意味着模型具有良好的性能。