金融领域的多层感知器（MLP）：应用与案例，数据驱动金融决策，创造价值

# 1. 多层感知器（MLP）概述

多层感知器（MLP）是一种前馈神经网络，广泛应用于金融领域。它由多个神经元层组成，每层神经元通过权重和偏置与下一层神经元相连。MLP的层级结构允许它学习复杂的数据模式，使其成为金融预测、风险评估和欺诈检测的有力工具。

MLP的训练过程涉及使用反向传播算法调整权重和偏置，以最小化损失函数。通过迭代训练，MLP可以学习从输入数据中提取特征，并对目标变量进行预测。

# 2. MLP理论基础

### 2.1 神经网络基础

#### 2.1.1 神经元模型

神经元是神经网络的基本组成单元，它模拟了人脑中神经元的行为。每个神经元接收多个输入信号，并通过激活函数生成一个输出信号。激活函数是一个非线性函数，它确定了神经元的输出与输入信号之间的关系。

常用的激活函数包括：

- Sigmoid 函数：`f(x) = 1 / (1 + e^(-x))`
- Tanh 函数：`f(x) = (e^x - e^(-x)) / (e^x + e^(-x))`
- ReLU 函数：`f(x) = max(0, x)`

#### 2.1.2 神经网络的结构和学习算法

神经网络由多层神经元组成，这些神经元以特定方式连接起来。最常见的网络结构是前馈神经网络，其中信息从输入层流向输出层，不涉及循环连接。

神经网络通过学习算法进行训练，以最小化输出信号与目标信号之间的误差。常用的学习算法包括：

- 反向传播算法：通过计算误差梯度并更新网络权重来迭代地优化网络。
- 梯度下降算法：通过沿着误差梯度下降的方向更新网络权重。

### 2.2 MLP的结构和原理

#### 2.2.1 MLP的层级结构

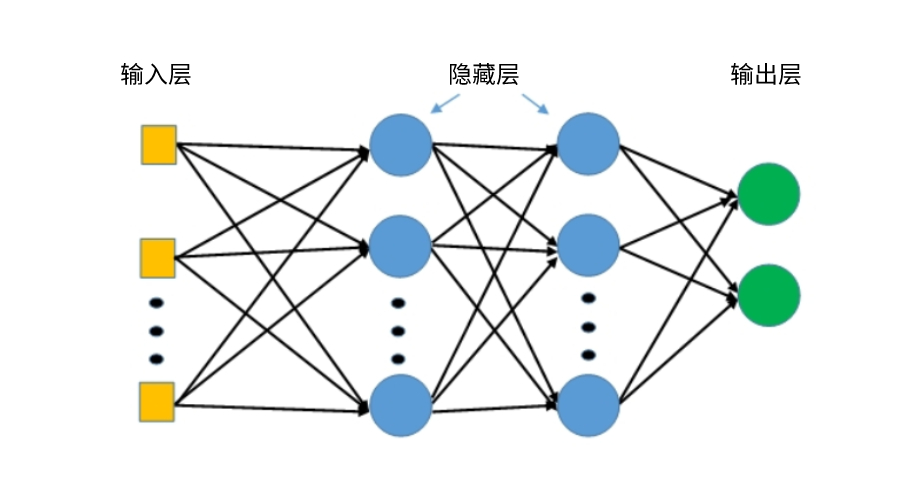
多层感知器（MLP）是一种前馈神经网络，它由输入层、输出层和多个隐藏层组成。输入层接收输入数据，输出层生成预测或分类结果，而隐藏层则在输入和输出之间进行非线性变换。

MLP的层级结构如下：

输入层 -> 隐藏层1 -> 隐藏层2 -> ... -> 隐藏层n -> 输出层

#### 2.2.2 MLP的训练过程

MLP的训练过程涉及以下步骤：

1. **前向传播：**输入数据通过网络从输入层传播到输出层，每个神经元根据其输入和激活函数计算其输出。
2. **误差计算：**输出层的神经元输出与目标值之间的误差被计算出来。
3. **反向传播：**误差通过网络从输出层反向传播到输入层，每个神经元的权重根据其输入、激活函数和误差梯度进行更新。
4. **权重更新：**更新后的权重用于前向传播过程，并重复上述步骤，直到误差达到可接受的水平。

**代码示例：**

import numpy as np

class MLP:
    def __init__(self, layers, activation):
        self.layers = layers
        self.activation = activation
        self.weights = [np.random.randn(n, m) for n, m in zip(layers[:-1], layers[1:])]
        self.biases = [np.zeros((n, 1)) for n in layers[1:]]

    def forward(self, X):
        for layer, weight, bias in zip(self.layers[1:], self.weights, self.biases):
            X = np.dot(X, weight) + bias
            X = self.activation(X)
        return X

    def train(self, X, y, epochs=100, batch_size=32, lr=0.01):
        for epoch in range(epochs):
            for i in range(0, len(X), batch_size):
                batch_X = X[i:i+batch_size]
                batch_y = y[i:i+batch_size]
                # 前向传播
                output = self.forward(batch_X)
                # 误差计算
                error = output - batch_y
                # 反向传播
                for layer in reversed(range(1, len(self.layers))):
                    weight = self.weights[layer-1]
                    bias = self.biases[layer-1]
                    # 计算梯度
                    d_error = error * self.activation.derivative(output)
                    d_weight = np.dot(batch_X.T, d_error)
                    d_bias = np.sum(d_error, axis=0, keepdims=True)
                    # 更新权重和偏置
                    weight -= lr * d_weight
                    bias -= lr * d_bias