残差连接与多层感知器（MLP）：深度网络训练利器，解决梯度消失，提升模型表现

# 1. 深度网络训练中的梯度消失问题

在深度神经网络训练中，随着网络层数的增加，梯度消失问题会变得愈发明显。这是因为在反向传播过程中，梯度会随着网络层数的增加而不断缩小，导致深层网络中的权重更新困难，从而影响模型的训练效果。

梯度消失问题的产生主要有以下几个原因：

* **激活函数的饱和性：**常用的激活函数（如 sigmoid、tanh）在输入较大或较小时会趋于饱和，导致梯度接近于 0。
* **权重初始化：**如果权重初始化不当，例如采用均匀分布或正态分布，可能会导致梯度消失。
* **网络层数过多：**随着网络层数的增加，梯度会经过更多的层，从而被不断缩小。

# 2. 残差连接的理论基础

### 2.1 残差网络的结构和原理

残差网络（ResNet）是一种深度神经网络，通过引入残差连接来解决梯度消失问题。残差连接将网络的输入和输出直接相连，从而允许梯度在网络中更有效地传播。

ResNet 的基本结构如下图所示：

graph LR
subgraph Input
    A[Input]
end
subgraph Hidden Layer
    B[Hidden Layer 1]
    C[Hidden Layer 2]
    D[Hidden Layer 3]
end
subgraph Output
    E[Output]
end
A --> B
B --> C
C --> D
D --> E
A --> E

其中，残差连接用虚线箭头表示，将输入 `A` 直接连接到输出 `E`。

### 2.2 残差连接的数学推导

假设一个残差块的输入为 `x`，输出为 `y`，则残差连接的数学表达式为：

y = x + F(x)

其中，`F(x)` 是残差块的非线性变换，通常由卷积层、激活函数和归一化层组成。

### 2.3 残差连接的优势和局限性

**优势：**

* **解决梯度消失问题：**残差连接允许梯度在网络中更有效地传播，从而缓解了梯度消失问题。
* **提高训练稳定性：**残差连接为网络提供了额外的路径，使训练过程更加稳定。
* **提升模型性能：**残差连接已被证明可以显著提高深度神经网络的性能，尤其是在图像分类和目标检测等任务中。

**局限性：**

* **增加计算成本：**残差连接需要额外的计算，这可能会增加模型的训练和推理时间。
* **可能引入冗余信息：**残差连接可能会引入冗余信息，这可能会降低模型的泛化能力。

# 3. 多层感知器（MLP）简介

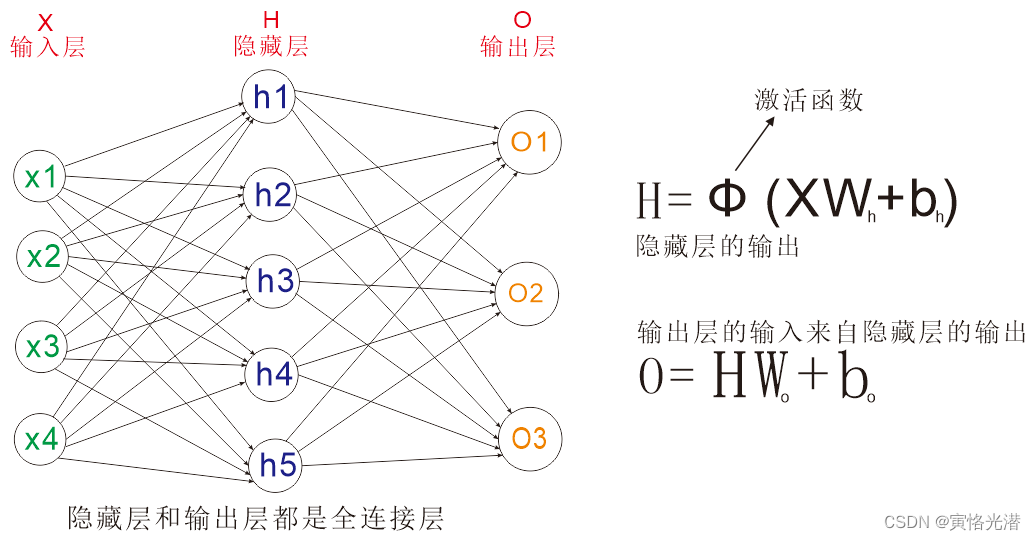
### 3.1 MLP的网络结构和前向传播

多层感知器（MLP）是一种前馈神经网络，由多个全连接层堆叠而成。MLP的网络结构如下图所示：

graph LR
subgraph 输入层
    A[输入层]
end
subgraph 隐含层
    B[隐含层 1]
    C[隐含层 2