并查集java在大规模数据处理中的优化策略

# 1. 简介

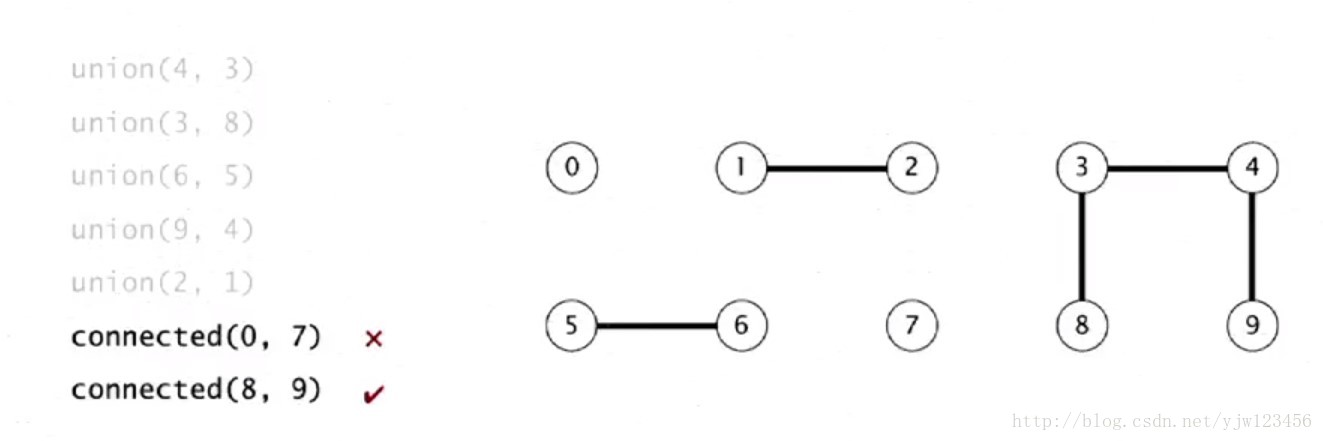
在计算机科学中，并查集（Disjoint Set）是一种数据结构，用于维护元素的分组情况。它提供了两个主要操作：查找（Find）和合并（Union）。在 Java 中，并查集通常通过数组实现，每个元素存储其父节点指针，用于表示元素之间的关系。并查集在解决图论、网络连接、最小生成树等问题中有着广泛的应用。通过查找和合并操作，可以快速判断两个元素是否属于同一组，实现数据的分类与聚合。在本文中，我们将深入探讨并查集的基本原理、操作方法和时间复杂度分析，帮助读者全面理解并查集数据结构在算法设计中的作用和应用场景。

# 2. 并查集的基本原理

#### 2.1 并查集数据结构

并查集（Disjoint Set）是一种用于处理集合合并和查询连通关系的数据结构。在并查集中，每个集合都被表示为一棵树。树的每个节点都存储一个元素，同时维护了指向父节点的指针或者父节点编号。并查集主要有两个关键操作：查找（Find）和合并（Union）。

##### 2.1.1 节点表示

在最简单的情况下，节点可以用整数数组来表示，并查集也可以实现成一个大小为 n 的整数数组，其中下标表示节点编号，数组元素存储该节点的根节点编号。当根节点编号等于节点编号时，这个节点就是一个集合的根节点。

##### 2.1.2 路径压缩

为了优化查找操作的性能，可以实现路径压缩。路径压缩是指在查找时，将搜索路径上的每个节点都直接连接到根节点，从而减少后续查找时需要遍历的路径长度，提高整体性能。

#### 2.2 并查集的基本操作

并查集的基本操作包括查找和合并。这两个操作是并查集维护集合的核心。

##### 2.2.1 查找操作

查找操作通常是通过递归或迭代的方式查找某个节点所在集合的根节点。同时进行路径压缩，将搜索路径上的节点直接连接到根节点，确保后续的查找更快。

int find(int[] parent, int x) {
    if (parent[x] != x) {
        parent[x] = find(parent, parent[x]);
    }
    return parent[x];
}

##### 2.2.2 合并操作

合并操作是将两个元素所在的集合合并为一个集合。通常选择其中一个元素的根节点作为两个集合的根节点。

void union(int[] parent, int x, int y) {
    int rootX = find(parent, x);
    int rootY = find(parent, y);
    if (rootX != rootY) {
        parent[rootX] = rootY;
    }
}

#### 2.3 并查集的时间复杂度分析

在不进行优化时，简单的并查集操作的时间复杂度为 O(n)，其中 n 表示节点的数量。查找操作的平均时间复杂度为 O(logn)，合并操作的时间复杂度也为 O(logn)。通过路径压缩和按秩合并等优化策略