深入探讨并查集java在图论算法中的应用

# 1. 图论算法基础入门

### 1.1 图的定义与基本概念
图是由顶点集合和边集合组成的数学结构。顶点表示图中的节点，边表示节点之间的关系。顶点和边可以携带额外信息，称为权重。图可以分为有向图和无向图，表示边的方向性。图的表示方法有邻接矩阵和邻接表等形式。

### 1.1.1 顶点和边的概念
图的顶点是节点的抽象，通常用数字或字符表示。边是连接顶点的线，可以带有权重。边的两个顶点称为端点。

### 1.1.2 图的类型与表示方法
常见图类型有无向图、有向图、加权图等。邻接矩阵适合稠密图，邻接表适合稀疏图。邻接表由顶点数组和邻接表链表构成。

在实际应用中，图论算法是解决各种问题的重要工具，包括网络路由、社交网络分析等。深入理解图的概念和表示方法有助于更好地应用图论算法解决实际问题。

# 2. 并查集数据结构详解

### 2.1 并查集基本原理

#### 2.1.1 并查集的概念与特点

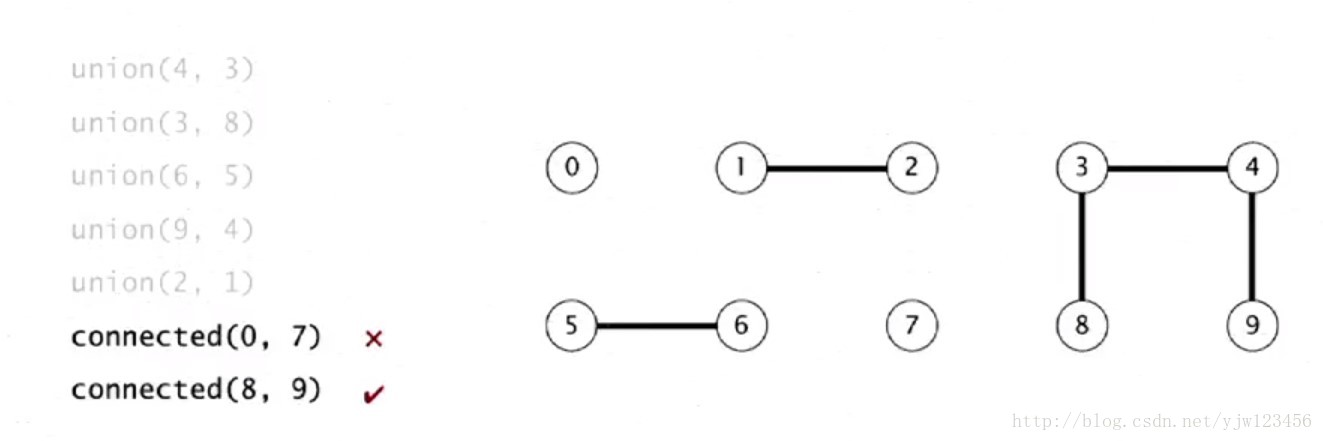
并查集（Disjoint Set）是一种用来处理不相交集合的数据结构。其主要支持两种操作：查找（Find）和合并（Union）。每个集合通过一个代表元（root）来标识，初始时每个元素自成一个集合，合并操作则是将两个集合通过它们的代表元合并为一个集合。并查集可以快速判断两个元素是否属于同一个集合，以及将不相交的集合合并为一个集合。

#### 2.1.2 并查集的实现方式

并查集的常见实现方式有基于树结构和基于数组结构两种。基于树结构的实现中，每个节点指向其父节点，树的根节点即为集合的代表元。在查找操作中通过递归找到根节点来判断两个元素是否属于同一集合；在合并操作中，将一个根节点作为另一个根节点的子节点即可完成合并。

基于数组结构的实现中，数组的索引代表元素，数组值代表父节点索引，即存储了每个元素所在集合的父节点索引。通过路径压缩和按秩合并等优化方式，可以提高并查集操作的效率。

### 2.2 并查集算法应用

#### 2.2.1 并查集在连通性问题中的应用

在连通性问题中，常用并查集来判断网络中节点的连通情况。通过判断两节点是否在同一个集合中，可以判断它们之间是否存在连通路径。这在网络连通性检测、岛屿数量统计等问题中有着广泛的应用。

#### 2.2.2 并查集在最小生成树算法中的应用

在最小生成树算法中，如Kruskal算法正是基于并查集实现的。通过构建初始状态下每个顶点独立的集合，并按边权值递增的顺序依次选择边，判断加入该边后是否形成环来实现最小生成树的构建。

#### 2.2.3 实际场景中的并查集应用案例

在实际应用中，并查集被广泛应用于社交网络中的好友关系判断、网站链接分析中的页面联通性分析、航空管制中的飞机航线优化等领域。通过并查集，可以快速判断元素之间的关系，简化问题的复杂度，提高算法效率。

以上是关于并查集数据结构的详尽解释，接下来，我们将深入探讨在Java语言中如何实现并查集，以及并查集的更多优化与扩展技巧。

# 3. Java语言中的并查集实现

- ### 3.1 Java中并查集的基本实现
- #### 3.1.1 实现并查集的数据结构
并查集是一种用于快速查找集合数据结构的算法，主要包括两个关键操作：查找和合并。在Java中，可以通过数组来表示并查集的数据结构。定义一个数组parent[]来存储每个元素的父节点，初始时父节点指向自身，即parent[i]=i。

    public class UnionFind {
        private int[] parent;
        public UnionFind(int size) {
            parent = new int[size];
            for (int i = 0; i < size; i++