基于并查集java的朋友圈关系问题求解

# 1. 理解并查集及其应用

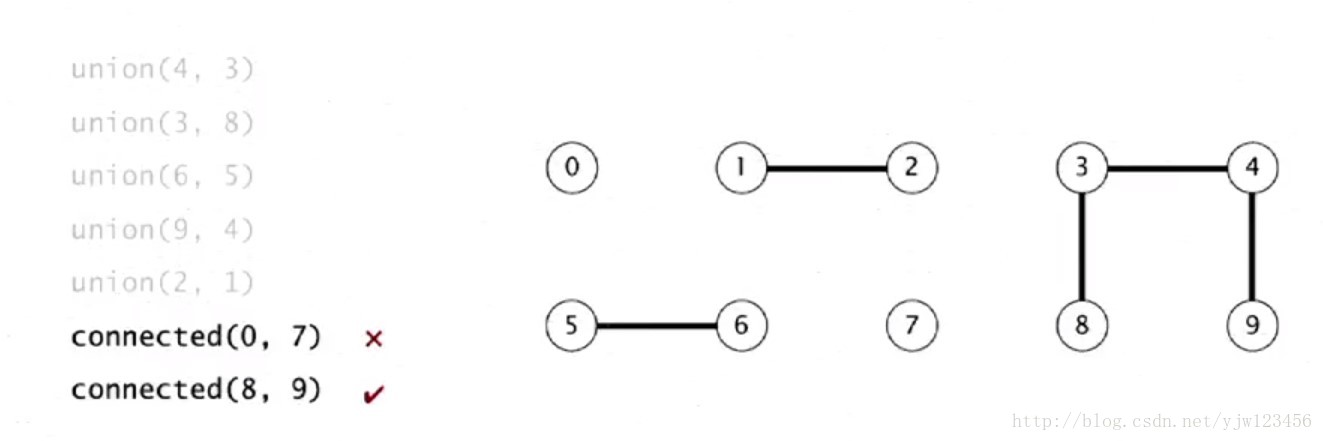
在计算机科学中，并查集（Disjoint Set）是一种数据结构，用于管理元素之间的等价关系。通过并查集，我们可以高效地合并集合、查询集合成员间的关系。其典型应用场景包括连接问题、朋友圈关系等。并查集的数据结构通常由一个数组构成，每个元素存储其父节点信息，通过路径压缩和按秩合并等优化策略，可以提高查询效率。在解决问题时，只需简单的几行代码即可实现并查集的基本功能。在实际应用中，比如在社交网络中维护朋友圈关系，使用并查集可以快速判断两人是否属于同一个朋友圈。深入理解并查集的原理和优化方法，对于解决实际问题具有重要意义。

# 2. 基本并查集算法实现

### 2.1 初始化并查集

在开始实现并查集算法之前，先创建一个数据结构来表示并查集。我们可以用数组来表示每个元素的父节点，初始时每个元素的父节点指向自身，表示各自为一个集合。同时，还需要一个 rank 数组来记录树的深度，用于优化合并操作。

### 2.2 查找根节点的路径压缩

实现查找操作时，需要找到节点的根节点，可以通过递归的方式实现路径压缩。在查找根节点的过程中，将树中所有节点直接连接到根节点上，以减少查找时间。

- **以下是 Java 代码实现：**

private int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

### 2.3 合并两个集合

合并两个集合时，需要找到两个元素的根节点，然后将其中一个根节点的父节点指向另一个根节点，以实现合并操作。在合并过程中，要考虑树的深度，将深度较小的树合并到深度较大的树上，以保持树的平衡。

- **以下是 Java 代码实现：**

private void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;