如何在并查集java中处理不相交集合

# 1. 介绍

- **了解并查集**
- 什么是并查集？
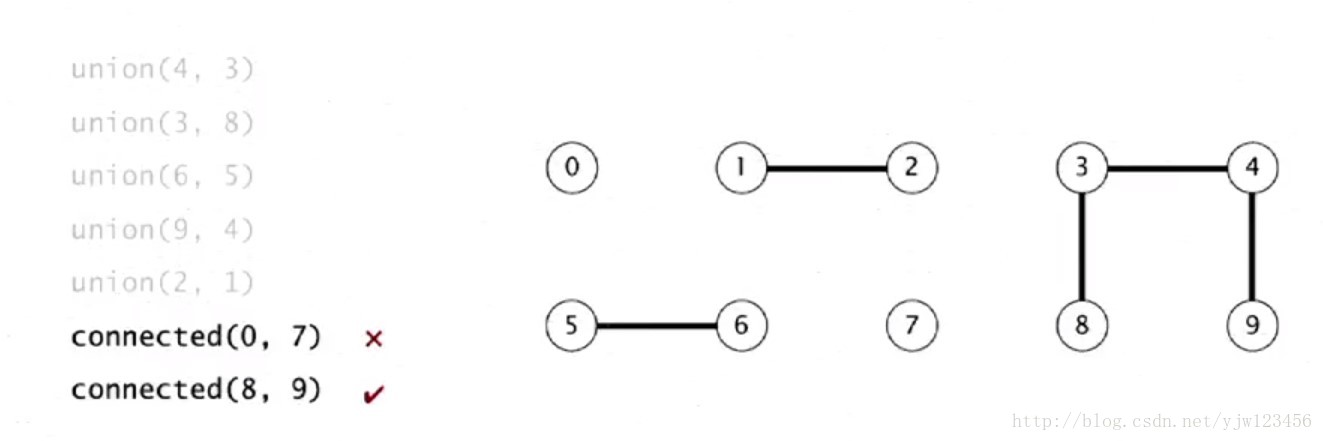
并查集是一种数据结构，用于解决元素分组的问题，主要支持两种操作：查找根节点和合并两个集合。通过跟踪元素之间的关系，可以快速判断它们是否属于同一组。

- 并查集的应用领域
并查集常用于图论、网络连接等领域。在实际应用中，可以用于解决岛屿数量计算、连通分量计算等问题。并查集的路径压缩和按秩合并优化策略也使其在大规模数据处理中具有优势。

# 2. 并查集的基本概念
#### 并查集数据结构
在并查集中，最基本的数据结构是一个节点数组，用来表示各个元素及其所属的集合。节点数组被初始化时，每个元素独立成为一个集合，即每个节点的父节点指向自身，表示该节点为集合的根节点。

#### 查找根节点的方法
要查找某个节点所在集合的根节点，需要沿着该节点的父节点一直向上查找，直到找到根节点，即父节点指向自身的节点。

#### 合并两个集合的方法
当需要合并两个集合时，实际上是将两个集合的根节点连接起来。详细步骤为：找到两个元素所在集合的根节点，然后将其中一个根节点的父节点指向另一个根节点。

#### 路径压缩优化
路径压缩是一种优化技巧，通过在查找根节点的过程中，将沿途经过的所有节点直接指向根节点，减少后续查找路径的长度，从而提高查找效率。

#### 如何实现路径压缩
实现路径压缩的关键在于，在查找根节点的过程中，将每个节点的父节点直接设为根节点，从而缩短后续查找路径的长度。

#### 路径压缩的时间复杂度分析
经过路径压缩优化后，单次查找的时间复杂度近似为 O(1)，因为每个节点的父节点直接指向根节点，快速找到集合的根节点。

#### 按秩合并优化
按秩合并是另一种优化技巧，通过维护每个集合的秩（即树的高度），在合并两个集合时，总是将秩较小的集合连接到秩较大的集合上。

#### 按秩合并的时间复杂度分析
通过按秩合并优化，可以保持树的平衡，避免出现较高的树，从而使得合并操作的时间复杂度近似为 O(1)。在每次合并时，通过比较秩的大小来决定合并方