并查集java在并行计算中的应用

# 1. 理解并查集

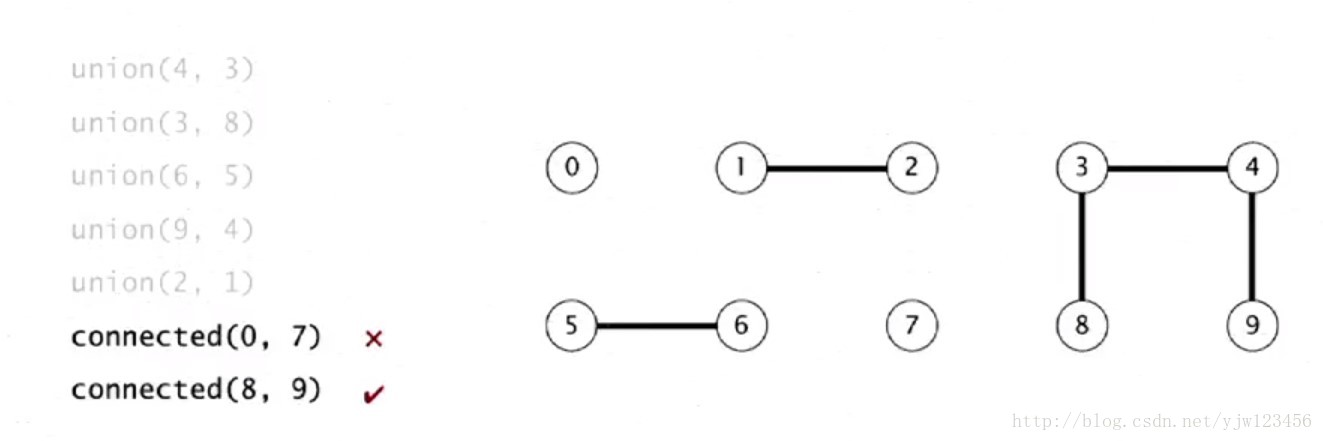
在计算机科学领域，**并查集**（Disjoint Set）是一种数据结构，用于维护元素的分组信息。它支持两种基本操作：**Find**（查找）和**Union**（合并）。通过这两个操作，我们可以快速判断两个元素是否属于同一组，或者将两个组合并为一个整体。

Find操作用于查找元素所属的组，通常通过递归遍历或路径压缩实现。Union操作用于将两个组合并，确保被合并的元素在同一个组内。并查集的应用十分广泛，例如在图论、网络连接、游戏中等领域。

通过理解并查集的基本操作，我们能够更好地解决组合问题，实现优化算法，并发挥其在并行计算中的潜力。

# 2. 并查集在Java中的实现

### 使用数组实现并查集
在Java中，可以使用数组来实现并查集的数据结构。首先，我们需要定义一个大小为N的整型数组来表示N个元素的集合，数组的索引表示元素的编号，数组中的值表示该元素所属的集合标识。初始时，每个元素都是单独的集合，集合标识可以是元素自身或者为-1。

### 优化：使用路径压缩和按秩合并
为了提高并查集的性能，在实现中可以使用路径压缩和按秩合并两种优化方式。路径压缩可以减少查找根节点时的时间复杂度，确保树高度降低到常数级别；按秩合并可以根据集合的深度进行合并，降低整体树的高度，提高查找和合并操作的效率。

public class UnionFind {
    private int[] parent;
    public UnionFind(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY;
        }
    }
}

以上代码演示了简单的并查集实现，包括初始化、查找根节点和合并操作。通过路径压缩和按秩合并的优化，可以大大提升并查集的效率和性能。

### 结论
通过数组实现并查集，并结合路径压缩和按秩合并的优化方式，可以在Java中高效地实现并查集数据结构，用于解决各种相关问题。

# 3. 并查集在并行计算中的基本原理

#### 并行计算的概念
并行计算是一种在同一时间执行多个计算任务的计算方式。这种计算方式通常用于处理大规模数据或执行需要高计算能力的任务。在并行计算中，任务被分解成多个子任务，这些子任务同时执行，提高了整体计算的效率。并行计算可以采用多种方式实现，如任务并行、数据并行、流水线并行等。

#### 并查集与并行计算的结合
并查集在并行计算中起着重要作用，特别是在处理图相关的问题时。并查集的并行性基于任务并行的思想，可以将不同的并查集操作并行执行，提高处理大规模数据集时的效率。通过合理设计并行计算方案，可以充分利用现代多核处理器的优势，加速并查集的运算过程。

#### 如何利用并行计算优