无向图中连通分量的计算与并查集java的关系

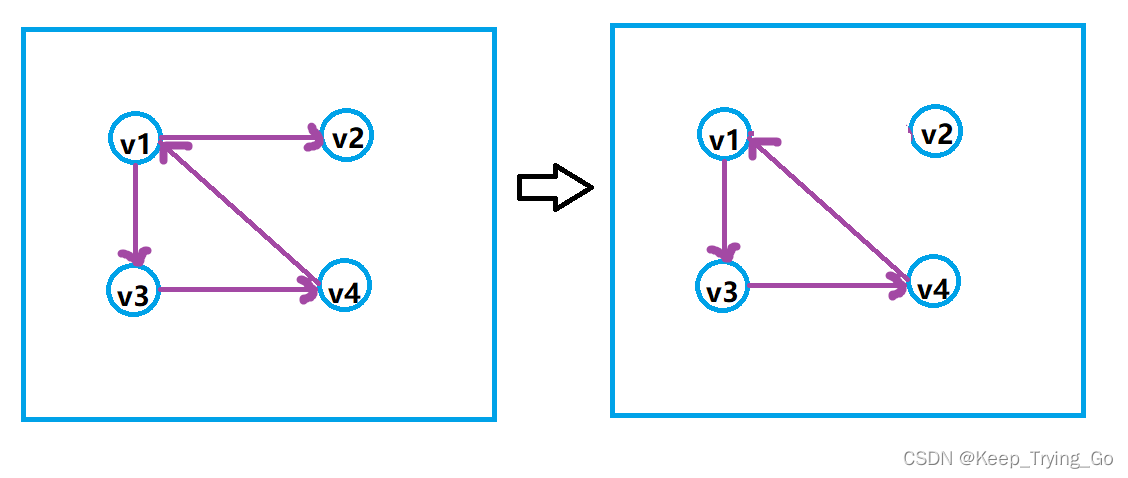
# 1. 图论中的连通性问题

1.1 无向图的基本概念

在图论中，无向图是由若干顶点和边组成的数据结构。顶点之间的边没有方向，因此表示为无序对。无向图可以使用邻接矩阵或邻接表来表示，方便进行遍历算法的实现。

图的遍历算法包括深度优先搜索（DFS）和广度优先搜索（BFS），它们可以用于查找图中的连通分量以及解决各种连通性问题。

1.2 连通图与连通分量

连通图是指图中任意两个顶点之间都存在路径的图。连通分量则是将连通图中相互连通的顶点分为一个集合，每个集合即为一个连通分量。

计算连通分量的方法包括DFS或BFS遍历整个图，并使用并查集来记录顶点之间的关系，以便在查找连通分量时进行快速检索。

# 2. 并查集数据结构

2.1 并查集简介
并查集（Disjoint Set）是一种基于树结构的数据结构，用于处理集合的合并与查询问题。在实际应用中，它通常用于解决元素分组及连通性等问题。并查集的核心操作包括查找（Find）和合并（Union）两种，通过这两种操作可以快速判断元素之间的关联关系，找出所属集合。

**2.1.1 并查集的概念**
并查集中的每个集合都被表示成树结构，其中的每个节点指向其父节点，根节点指向自身。通过路径压缩和按秩合并等优化方式，可以提高并查集的效率，降低树的深度，减少查找操作的时间复杂度。

**2.1.2 并查集的应用场景**
- 社交网络中的好友关系判断
- 电子游戏中的联盟系统
- 区域连通性分析
- 网络中的设备连接状态判断

2.2 并查集的实现
并查集主要有三种实现方式：Quick Find算法、Quick Union算法和加权Quick Union算法。

**2.2.1 Quick Find算法**
Quick Find算法是并查集最简单的实现方式，通过一个数组来维护集合的信息。根据元素所在集合的不同，将数组中对应位置的值进行不同的设置。

    class QuickFind:
        def __init__(self, n):
            self.parent = [i for i in range(n)]

        def find(self, p):
            return self.parent[p]
        def union(self, p, q):
            p_root = self.find(p)
            q_root = self.find(q)
            if p_root == q_root:
                return
            for i in range(len(self.parent)):
                if self.parent[i] == p_root:
                    self.parent[i] = q_root

**2.2.2 Quick Union算法**
Quick Union算法基于树结构实现，并通过节点之间的父子关系来表示集合间的连接情况。这种实现方式在合并操作时，将一个集合的根节点指向另一个集合的根节点。

    class QuickUnion:
        def __init__(self, n):
            self.parent = [i for i in range(n)]

        def find(self, p):
            while p != self.parent[p]:
                p = self.parent[p]
            return p
        def union(self, p, q):
            p_root = self.find(p)
            q_root = self.find(q)
            if p_root == q_root:
                return
            self.parent[p_root] = q_root

**2.2.3 加权Quick Union算法**
加权Quick Union算法在Quick Union基础上进行了优化，通过维护每个根节点的子节点数量（权值），在合并操作时总是将节点少的树合并到节点多的树上，以降低树的深度，提高查找效率。

    class WeightedQuickUnion:
        def __init__(self, n):
            self.parent = [i for i in range(n)]
            self.size = [1] * n

        def find(self, p):
            while p != self.parent[p]:
                p = self.parent[p]
            return p
        def union(self, p, q):
            p_root = self.find(p)
            q_root = self.find(q)
            if p_root == q_root:
                return
            if self.size[p_root] < self.size[q_root]:
                self.parent[p_root] = q_root
                self.size[q_root] += self.size[p_root]
            else:
                self.parent[q_root] = p_root
                self.size[p_root] += self.size[q_root]

2.3 并查集的优