如何处理并查集java中的环路检测

# 1. 介绍

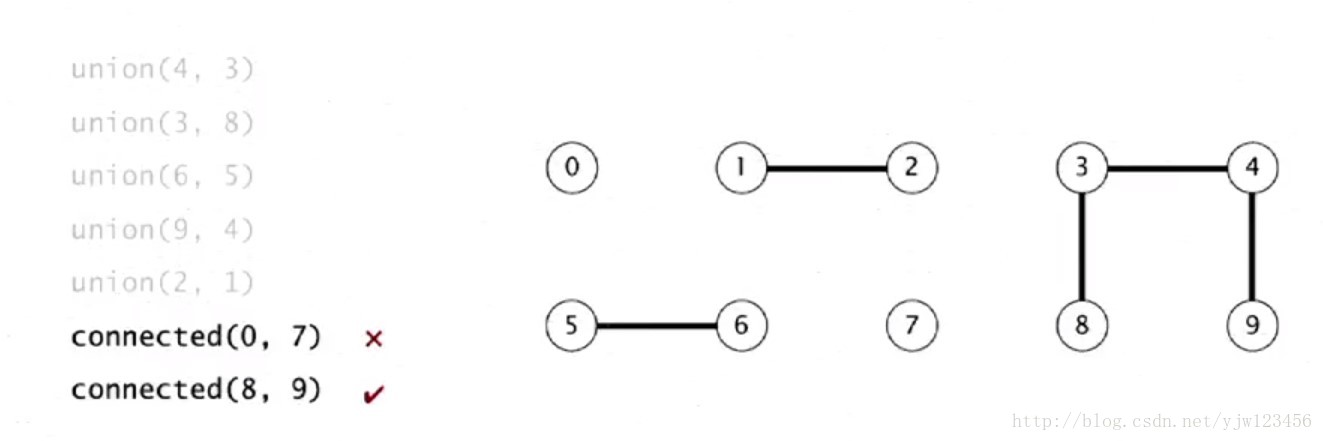
在计算机科学中，**并查集**（Disjoint Set）是一种数据结构，用来维护元素的分组情况。它主要用于解决集合的合并与划分等问题，其中环路检测是其中一个重要的应用场景。通过并查集，我们可以高效地管理元素之间的关系，快速找到它们所属的组别，从而在需要时进行合并操作。环路检测在图论领域中有着广泛的应用，可以帮助我们及时发现图中是否存在环路，避免数据处理过程中出现错误的情况。通过深入理解并查集的基本概念和环路检测算法，我们可以更好地应用这一数据结构，提高程序的效率和准确性。

# 2. 并查集的基本概念

并查集（Disjoint Set）是一种用来管理元素分组的数据结构，常用于解决图论中的连通性问题。在并查集中，每个集合被表示成一棵树，树根表示该集合的标识符。在本章节中，我们将详细介绍并查集的基本概念和关键操作。

#### 树形结构的表示

在并查集中，每个元素都被表示成一个树，其中根结点代表集合的标识符。根结点的特点是指向自身，可以通过不断向上查找父节点，直到根节点来确定所属集合。

- 根结点的确定

在初始化时，每个元素自成一个集合，根据需要，当合并两个集合时，选择其中一个根节点作为另一个的父节点，以确保集合的合并。

- 路径压缩算法

为了提高查询效率，在查找根节点时，可以利用路径压缩算法，使得查找路径上的每个节点都指向根节点，从而降低树的深度，提高后续查找的效率。

#### 合并操作

在并查集中，最重要的操作是合并操作和查找操作。合并操作用于将两个集合合并，而查找操作用于找到一个元素所属的集合。

- `union()` 方法

`union()` 方法用于合并两个集合，即将其中一个集合的根节点指向另一个集合的根节点，从而实现集合的合并。

- `find()` 方法

`find()` 方法用于查找一个元素所属的集合，通过不断向上查找父节点直到根节点来确定。

- 路径压缩的实现

路径压缩是通过在查找时将路径上的每个节点都