快速合并算法在并查集java中的应用

# 1.1 什么是并查集

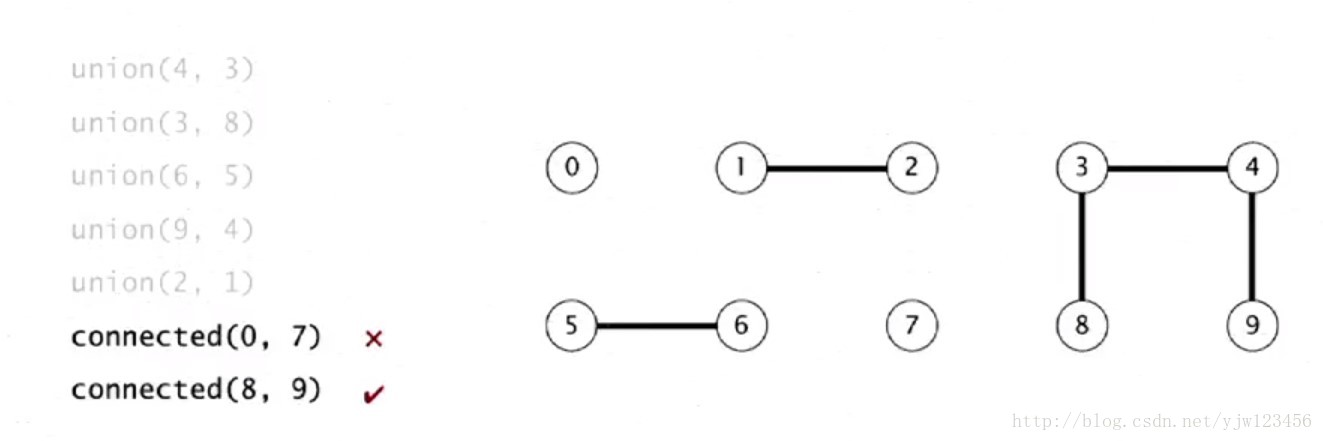
并查集是一种用于处理集合的数据结构，主要用于解决元素的分组问题。其基本概念包括集合的表示和元素之间的关联关系。并查集的特点在于能够快速进行查找和合并操作，使得在处理连通性问题时具有高效性能。

### 1.1.1 并查集的基本概念

在并查集中，每个元素属于一个集合，通过代表元素表示整个集合，同一集合内的元素具有相同的代表元素。通过查找操作可以确定元素所属的集合，合并操作可以将两个集合合并为一个集合。

### 1.1.2 并查集的特点

并查集的特点在于快速的查找和合并操作，通常能够在近乎常数时间内完成。此外，并查集还具有简单易懂的数据结构和操作方式，适用于各种连通性和分组性问题的解决。

# 2. 并查集的经典实现

- **2.1 实现并查集的数据结构**

并查集（Disjoint Set）是一种数据结构，用于处理一些不相交集合的合并及查询问题。它的基本操作包括查找元素属于哪个集合以及合并两个集合。在并查集中，每个集合通常用一棵树来表示，树的每个节点指向其父节点，根节点代表集合的标识。

- **2.1.1 使用数组表示并查集**

在实现并查集时最简单的方式是使用一个数组来表示每个元素所属的集合。我们可以用一个大小为n的数组`parent[]`来保存每个元素的父节点，初始时每个元素的父节点指向自己。

class UnionFind {
    private int[] parent;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
}

- **2.1.2 路径压缩和按秩合并优化**

为了优化并查集的性能，可以使用路径压缩和按秩合并两种优化方式。路径压缩是指在查找根节点的过程中，将沿途经过的所有节点直接连接到根节点上，从而降低树的高度。按秩合并是指将“树”更矮的集合合并到“树”更高的集合上。

class UnionFind {
    private int[] parent;
    private int[] rank;

    public UnionFind(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }
}

- **2.2 并查集的应用**

并查集在各种算法和问题中有广泛的应用，其中一些典型的应用包括连通性问题、最小生成树算法中的应用以及在社交网络中的应用。

- **2.2.1 连通性问题**

在连通性问题中，需要判断两个节点是否连通。通过并查集，可以快速查找节点所属的集合，进而判断它们是否连通。

- **2.2.2 最小生成树算法中的应用**

在最小生成树算法中，如Kruskal算法和Prim算法，需要处理边的连通性以构建最小生成树。并查集可以有效地判断是否存在环路，并用于边的合并操作。

- **2.2.3 社交网络中的应用**

在一个社交网络中，可以用并查集来管理人际关系。通过并查集，可以快速找到一个人的朋友圈，也可以判断两人是否在同一个朋友圈内。

# 3. 快速合并算法详解

- **3.1 Quick Union 算法**
- **3.1.1 算法思路简介**
Quick Union 算法是一种基于树形结构的并查集实现方式，每个节点都指向其父节点，形成一棵树。合并操作时，只需将一个集合的根节点指向另一个集合的根节点即可。
- **3.1.2 实现方式及优缺点**
Quick Union 算法的实现相对简单，主要涉及两个核心操作：查找根节点和合并两个集合。但是在最坏情况下，树的高度可能会达到 n，导致查找操作的时间复杂度为 O(n)。
- **3.2 路