如何有效应对并查集java中的性能问题

# 1. 概述

在计算机科学中，性能优化是一项至关重要的工作，涉及到数据结构、算法复杂度、代码实现等多个方面。对于并查集这种常用的数据结构而言，优化性能尤为关键。本文将深入探讨并查集性能优化的策略与方法。

在研究并查集性能问题时，我们需要理解路径压缩、按秩合并等优化策略的原理，以及它们在实际应用中的效果。此外，对于大规模数据的处理和代码实现的优化也不容忽视。性能测试工具的选择与性能评估也是优化过程中的重要环节。

通过本文的详细探讨，读者将能够更好地理解并查集性能优化的重要性，掌握优化策略的实际应用，进而在实际开发中提升算法效率，提升系统性能。

# 2. 性能问题的根源

在设计和实现一个系统时，性能问题往往是程序员需要面对的挑战之一。了解性能问题的根源对于有效优化系统至关重要。在这一章节中，我们将深入探讨性能问题的根源，包括数据结构选择的重要性以及算法复杂度分析。

#### 2.1 数据结构选择的重要性

数据结构是程序的基础，合适的数据结构可以提高程序的效率。在处理大规模数据时，选择合适的数据结构显得尤为重要。常见的数据结构包括数组、链表、树、图等，它们各自适用于不同的场景。

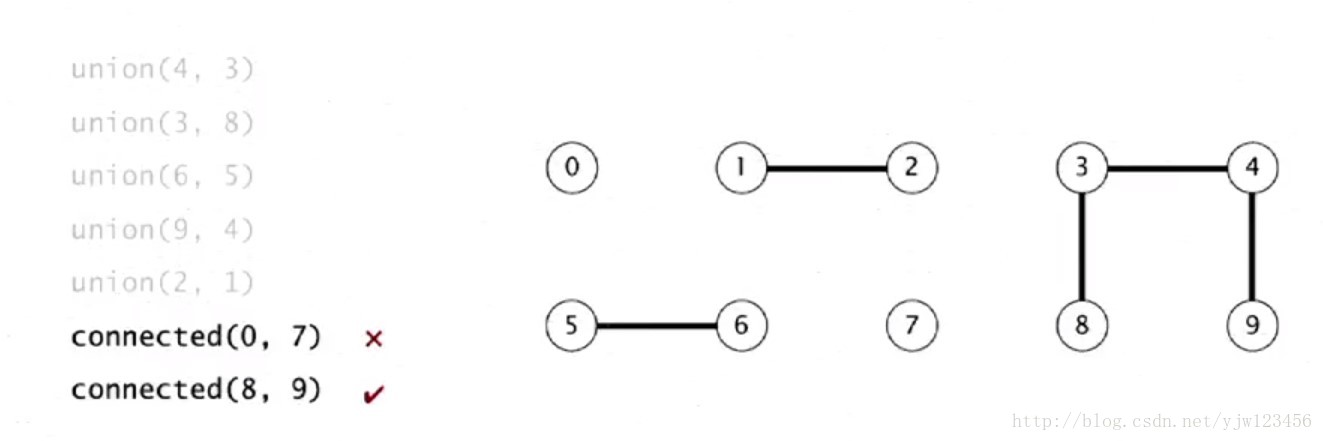
在并查集这样的场景中，选择合适的数据结构能够有效减少时间复杂度，提高系统的性能。并查集通常使用数组或树结构来表示不相交集合，合理选择数据结构能够在查找、连接、合并等操作中实现更高效的性能。

#### 2.2 算法复杂度分析

在解决性能问题时，算法的复杂度是一个至关重要的考量因素。算法复杂度通常包括时间复杂度和空间复杂度两个方面，它们直接影响着程序的执行效率和资源消耗。

##### 2.2.1 时间复杂度

时间复杂度是衡量算法执行效率的一个重要指标，通常用大 O 表示。常见的时间复杂度包括 O(1)、O(logn)、O(n)、O(nlogn)、O(n²) 等，不同时间复杂度的算法在处理大规模数据时表现出不同的效率。

在并查集中，路径压缩和按秩合并等优化方式可以降低算法的时间复杂度，提升系统性能。

##### 2.2.2 空间复杂度

空间复杂度则是评估算法所需存储空间大小的指标，