【神经网络调参攻略】：成为调参大师的不传之秘

# 1. 神经网络调参基础

在神经网络模型的训练过程中，调参是一项至关重要且充满挑战的工作。良好的调参策略能够显著提升模型的性能，而不良的调参则可能导致模型无法有效学习数据特征，甚至无法收敛。本章将从基础出发，为读者展开神经网络调参的世界。

首先，我们探讨调参的必要性。神经网络由大量参数组成，包括权重(weight)、偏差(bias)和学习率(learning rate)，调整这些参数是确保模型能够从数据中学习到有用信息的关键步骤。接着，我们将介绍一些基本的调参原则，包括对模型过拟合与欠拟合的认识、如何设置合适的学习率以及批量大小(batch size)对训练过程的影响。

最后，本章还将提供一些通用的调参技巧，这些技巧来源于实践经验，可以作为读者在面对具体问题时的参考。通过本章内容的学习，读者将对神经网络调参有一个初步的认识，并为深入理解和应用后续章节内容打下坚实的基础。

# 2. 理解神经网络中的权重和偏差

在构建和训练神经网络时，权重（weights）和偏差（biases）是构建模型的基本组件。它们是构成神经网络参数的核心，并在训练过程中不断更新以最小化损失函数。理解这些概念对于优化模型性能至关重要。

## 2.1 权重和偏差的理论基础

### 2.1.1 权重和偏差的数学定义

权重和偏差是线性变换的组成部分，用于在神经网络中进行特征的加权求和。权重决定了输入特征在计算中所占的重要性，而偏差则提供了函数的平移能力。在数学上，权重可以看作是连接两个神经元的边的强度，而偏差则可以看作是神经元激活的阈值。

在矩阵表示中，权重可以表示为一个矩阵W，其中每个元素wij表示从输入单元i到输出单元j的连接权重。偏差通常用向量b来表示，其中每个元素bj是对应于输出单元j的偏差项。

### 2.1.2 权重和偏差在模型中的作用

在神经网络中，权重和偏差共同定义了从输入到输出的映射关系。权重负责捕捉输入特征之间的线性关系，而偏差则帮助调整神经元的激活水平。权重较大的连接意味着模型会更加重视对应的输入特征，而偏差则为模型提供了一定的灵活性，使得即使在没有输入的情况下，神经元也有可能被激活。

## 2.2 初始化权重和偏差的最佳实践

初始化权重和偏差是训练神经网络的第一步。正确的初始化方法可以帮助模型更快地收敛，并可能提高最终的性能。

### 2.2.1 随机初始化的策略

随机初始化是将权重初始化为小的随机数。它帮助确保网络中的每个神经元在开始时都是唯一的，这样可以打破对称性，促进梯度下降过程中权重的差异性更新。Xavier初始化和He初始化是两种常用的随机初始化策略，它们特别适用于不同类型的网络层。

以下是Xavier初始化的伪代码示例：

import numpy as np

def xavier_init(input_dim, output_dim):
    # 计算fan_in和fan_out
    fan_in = input_dim
    fan_out = output_dim
    # 计算Xavier初始化的缩放因子
    scale = np.sqrt(2.0 / (fan_in + fan_out))
    # 随机初始化权重
    W = scale * np.random.randn(input_dim, output_dim)
    return W

这里，权重初始化是基于输入层和输出层的单元数来计算缩放因子的，以保持激活分布的方差在前向和反向传播过程中的一致性。

### 2.2.2 预训练和微调的初始化方法

对于深度神经网络而言，逐层预训练可以帮助解决深层网络的梯度消失或爆炸问题。预训练是一个自底向上的过程，每一层在预训练时都被初始化以捕捉输入数据的复杂特征。

接着，可以使用微调方法，其中预训练模型的权重作为新任务的起点。通过在目标任务上进一步训练，可以调整权重以更好地适应新任务。

在微调时，通常只对最后几层进行训练，因为这些层更可能学习到与特定任务相关的特征。而前几层学习到的低级特征在很多任务中是通用的。

# 假设已经有一个预训练的模型pretrained_model和数据集new_dataset
import copy

# 冻结预训练模型的权重
for param in pretrained_model.parameters():
    param.requires_grad = False

# 新增顶层，用于微调
fine_tuned_model = copy.deepcopy(pretrained_model)
fine_tuned_model.add_module('new_layer', torch.nn.Linear(...))

# 只对新增顶层进行训练
optimizer = torch.optim.Adam(fine_tuned_model.parameters())
for epoch in range(num_epochs):
    optimizer.zero_grad()
    output = fine_tuned_model(new_dataset)
    loss = compute_loss(output)
    loss.backward()
    optimizer.step()

在上述代码中，我们首先复制了一个预训练的模型，并添加了新的顶层。随后，我们只更新这个顶层的参数，以对特定的新任务进行微调。这种策略能够保留预训练模型已学习的知识，并通过新增层来适应新任务。

权重和偏差作为神经网络中的核心参数，通过不同的初始化方法可以有效地影响模型的学习过程。正确地理解这些参数的作用并应用合适的初始化策略，对于设计高效的神经网络模型至关重要。在下一节中，我们将探讨激活函数与损失函数的选择，这些也是构建有效神经网络架构时不可或缺的部分。

# 3. 激活函数与损失函数的选择

激活函数和损失函数是神经网络设计的两个核心组成部分，它们各自扮演着至关重要的角色。激活函数负责引入非线性，使得神经网络能够解决复杂的问题，而损失函数则用于评估模型的性能，指导模型的训练方向。理解它们的类型、特点以及适用场景是进行神经网络调参时不可或缺的环节。

## 3.1 激活函数的类型和适用场景

### 3.1.1 常见激活函数的比较

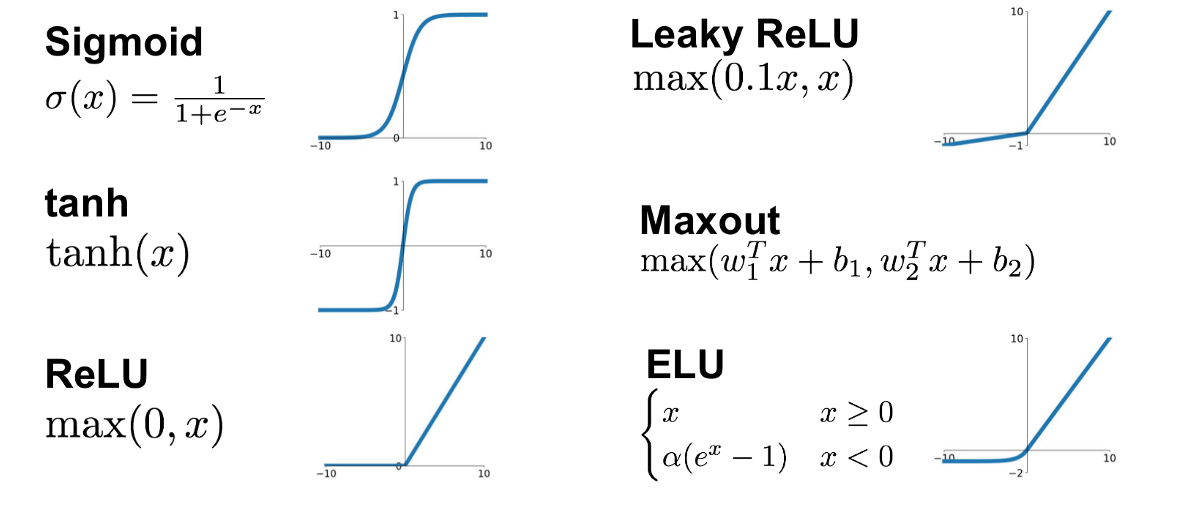
在神经网络中，激活函数的选择对模型的性能有着直接影响。以下是几种常见的激活函数及其特点的比较：

- **Sigmoid函数**：S型的激活函数，输出范围在0到1之间，常用于二分类问题的输出层。然而，由于其梯度消失问题，不建议用于隐藏层。
- **Tanh函数**：与Sigmoid类似，但是输出范围是-1到1，中间的零点对称。Tanh比Sigmoid更适合隐藏层，但同样存在梯度消失的问题。

- **ReLU函数**：线性整流单元（Rectified Linear Unit），如果输入为正则输出为输入本身，否则输出为0。ReL