多元线性回归变量转换技巧：提升模型性能，揭示数据隐藏价值

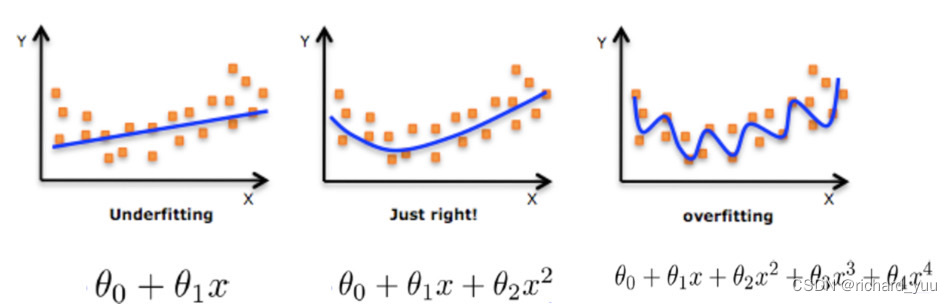
# 1. 多元线性回归简介

多元线性回归是一种统计建模技术，用于预测一个或多个连续型因变量（响应变量）与多个自变量（预测变量）之间的关系。它基于以下线性方程：

y = β0 + β1x1 + β2x2 + ... + βpxp + ε

其中：

* y 是因变量
* x1, x2, ..., xp 是自变量
* β0, β1, ..., βp 是回归系数
* ε 是误差项

多元线性回归通过最小化误差项的平方和来估计回归系数。它是一种强大的工具，可用于识别自变量与因变量之间的关系，并预测因变量的未来值。

# 2. 变量转换的理论基础

### 2.1 变量转换的目的和类型

变量转换是一种数据预处理技术，其目的是通过对原始变量进行数学变换，改善模型的拟合度和预测能力。变量转换的类型主要有：

- **线性转换：**将变量乘以一个常数或加上一个常数，如标准化和中心化。
- **非线性转换：**对变量进行非线性变换，如对数转换、平方根转换和Box-Cox转换。
- **二值化：**将连续变量转换为二元变量，如大于某一阈值则为1，否则为0。
- **独热编码：**将分类变量转换为一组二元变量，每个变量表示一个类别。
- **因子变量编码：**将分类变量转换为一组连续变量，每个变量表示一个类别。

### 2.2 变量转换的数学原理

变量转换的数学原理主要基于以下几个方面：

- **分布变换：**通过转换改变变量的分布，使其更接近正态分布或其他理想分布。
- **线性关系：**通过线性转换消除变量之间的共线性，改善模型的稳定性。
- **非线性关系：**通过非线性转换捕捉变量之间的非线性关系，提高模型的预测能力。
- **变量缩放：**通过缩放转换将变量的取值范围调整到相同水平，避免某些变量对模型的影响过大。

### 代码示例

以下代码示例展示了对数值变量进行对数转换：

import numpy as np
import pandas as pd

# 原始数据
data = pd.DataFrame({
    "age": [20, 30, 40, 50, 60],
    "income": [10000, 20000, 30000, 40000, 50000]
})

# 对 "income" 列进行对数转换
data["log_income"] = np.log(data["income"])

# 打印转换后的数据
print(data)

**代码逻辑分析：**

1. 导入必要的库。
2. 创建一个包含 "age" 和 "income" 列的 DataFrame。
3. 使用 `np.log()` 函数对 "income" 列进行对数转换，并将其存储在新的列 "log_income" 中。
4. 打印转换后的 DataFrame。

**参数说明：**

- `np.log()`: 对输入数组中的每个元素进行自然对数转换。
- `data["income"]`: 要转换的原始 "income" 列。
- `data["log_income"]`: 存储转换后结果的新列。

# 3. 变量转换的实践应用

### 3.1 数值变量的转换

数值变量的转