MATLAB多元线性回归主成分分析详解：降维和特征提取，提升模型效率

# 1. 多元线性回归简介**

多元线性回归是一种统计建模技术，用于预测一个或多个自变量（x）与一个因变量（y）之间的线性关系。它通过拟合一条直线或平面来近似数据，并使用该模型来预测新数据点的因变量值。

多元线性回归模型的数学形式为：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y 是因变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是模型参数
* ε 是误差项

多元线性回归广泛应用于各种领域，包括预测、建模和数据分析。它可以帮助理解自变量和因变量之间的关系，并用于预测未来值。

# 2. 主成分分析理论基础**

**2.1 主成分分析的数学原理**

**2.1.1 协方差矩阵和特征值分解**

主成分分析的核心在于对数据的协方差矩阵进行特征值分解。协方差矩阵衡量了数据集中不同变量之间的相关性。

设数据集包含n个样本，m个变量，则协方差矩阵C定义为：

C = 1/(n-1) * X^T * X

其中，X是数据矩阵，X^T是X的转置。

特征值分解将协方差矩阵分解为一组特征值和特征向量。特征值表示协方差矩阵沿不同方向的方差，而特征向量表示这些方向。

**2.1.2 主成分的计算和解释**

主成分是协方差矩阵特征向量对应的线性组合。第i个主成分由以下公式计算：

PC_i = X * V_i

其中，V_i是协方差矩阵的第i个特征向量。

主成分的方差等于对应的特征值，因此方差最大的主成分捕捉了数据中最大的方差。主成分的解释由其对应的特征向量决定。特征向量中的元素表示不同变量在该主成分中的贡献。

**2.2 主成分分析的降维作用**

**2.2.1 数据可视化和理解**

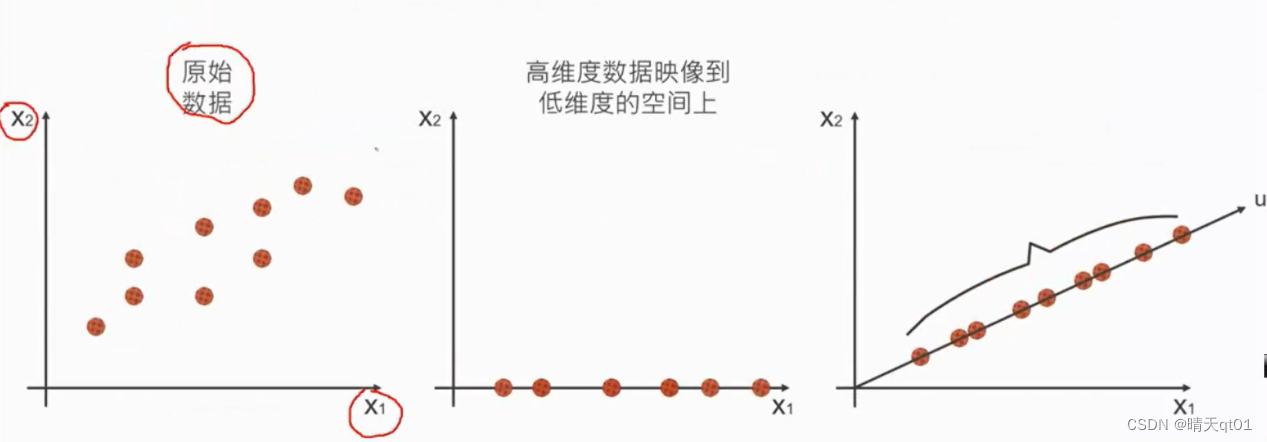
主成分分析可以将高维数据投影到低维空间，从而简化数据可视化和理解。例如，对于一个包含10个变量的数据集，主成分分析可以将数据投影到2维或3维空间，以便于绘制散点图或3D图形。

**2.2.2 冗余信息的去除**

主成分分析可以去除数据中的冗余信息。协方差矩阵的特征值表示数据中不同方向的方差。如果两个变量高度相关，则它们将具有相似的特征向量，并且可以由一个主成分表示。通过去除冗余信息，主成分分析可以减少数据的维度，同时保留最重要的信息。

# 3. MATLAB中主成分分析实践

### 3.1 数据预处理和主成分提取

#### 3.1.1 数据标准化和中心化

在进行主成分分析之前，需要对数据进行预处理，包括标准化和中心化。标准化将数据转换为均值为0、标准差为1的标准正态分布，从而消除不同特征量纲的影响。中心化将数据中心化为0，即减去每个特征的均值。

% 假设 data 为原始数据，特征数量为 p
[n, p] = size(data);

% 标准化
data_std = (data - mean(data)) ./ std(data);

% 中心化
data_centered = data - mean(data);

#### 3.1.2 使用MATLAB函数提取主成分

MATLAB提供了 `pca` 函数用于提取主成分。该函数返回主成分矩阵 `U`，其中每一列对应一个主成分，以及主成分的方差贡献率 `eigvals`。