MATLAB多元线性回归非线性关系处理秘籍：多项式回归和核函数，扩展模型适用范围

# 1. 多元线性回归简介

多元线性回归是一种统计模型，用于预测一个连续的因变量（目标变量）与多个自变量（预测变量）之间的关系。它假设因变量和自变量之间的关系是线性的，即自变量的变化会以恒定的速率影响因变量。

多元线性回归模型的方程为：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y 是因变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是模型系数
* ε 是误差项，表示模型无法解释的因变量的变化

# 2. 多元线性回归非线性关系处理

在现实世界中，许多数据呈现出非线性关系，而多元线性回归模型假设变量之间存在线性关系。为了处理非线性关系，有两种常用的技术：多项式回归和核函数。

### 2.1 多项式回归

#### 2.1.1 多项式回归的原理

多项式回归通过将自变量提升到更高的幂次来拟合非线性关系。假设我们有一个多元线性回归模型：

y = β0 + β1x1 + β2x2 + ... + βnxn

其中，y是因变量，x1、x2、...、xn是自变量，β0、β1、...、βn是模型参数。

多项式回归将自变量提升到d次幂，得到一个d次多项式模型：

y = β0 + β1x1 + β2x1^2 + ... + βd+1x1^d + βd+2x2 + βd+3x2^2 + ... + βd+n+1x2^d + ... + βd+n+1xn^d

通过增加多项式的次数，模型可以拟合更复杂的非线性关系。

#### 2.1.2 多项式回归的模型选择和评估

选择合适的多项式次数至关重要。次数太低可能无法拟合非线性关系，而次数太高可能导致过拟合。

模型选择可以使用以下方法：

- **交叉验证：**将数据集分成训练集和测试集，使用训练集拟合不同次数的多项式模型，然后在测试集上评估模型的性能。
- **AIC（赤池信息准则）：**一种模型选择准则，它考虑了模型的拟合度和复杂度。AIC较小的模型更优。

模型评估可以使用以下指标：

- **均方误差（MSE）：**预测值与真实值之间的平均平方差。
- **决定系数（R^2）：**模型拟合程度的度量，取值范围为0到1，1表示完美拟合。

### 2.2 核函数

#### 2.2.1 核函数的原理

核函数是一种将非线性数据映射到高维特征空间的技术，从而使数据在高维空间中线性可分。

核函数K(x, y)定义了两个数据点x和y在特征空间中的相似度。常用的核函数有：

- **线性核：**K(x, y) = x^T y
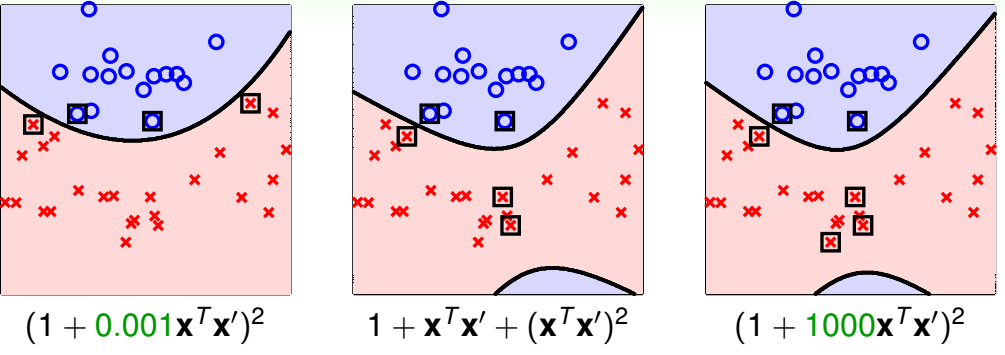
- **多项式核：**K(x, y) = (x^T y + c)^d
- **径向基核：**K(x, y) = exp(-γ||x - y||^2)

其中，c和γ是核函数的参数。

#### 2.2.2 常用核函数的类型和选择

不同的核函数适用于不同的数据类型和任务。

| 核函数 | 优点 | 缺点 |
|---|---|---|
| 线性核 | 计算简单 | 仅适用于线性可分的数据 |
| 多项式核 | 可以拟合复杂非线性关系 | 容易过拟合 |
| 径向基核 | 适用于高维数据 | 参数选择较困难 |

核函数的选择取决于数据的性质和任务的目标。

# 3. MATLAB中多项式回归和核函数的实现

### 3.1 多项式回归的实现

#### 3.1.1 多项式模型的拟合

在MATLAB中，可以使用`polyfit`函数拟合多项式模型。该函数的语法如下：

p = polyfit(x, y, n)

其中：

* `x`：输入特征向量
* `y`：输出目标向量
* `n`：多项式的阶数

`polyfit`函数返回一个包含多项式系数的向量`p`。系数`p(1)`对应于最高阶项，`p(end)`对应于常数项。

例如，拟合一个二次多项式模型：

x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];
p = polyfit(x, y, 2);

拟合后的模型为：

y = 2 + 4x + 8x^2

#### 3.1.2 模型评估和预测

拟合多项式模型后，可以使用`polyval`函数评估模型并进行预测。`polyval`函数的语法如下：

y = polyval(p, x)

其中：

* `p`：多项式系数向量
* `x`：输入特征向量

`polyval`函数返回一个包含预测值`y`的向量。

例如，使用拟合的二次多项式模型预测`x = 6`时的输出：

y_pred = polyval(p, 6);

预测值`y_pred`为50。

### 3.2 核函数的实现

#### 3.2.1 核函数的应用

在MATLAB中，可以使用`fitcknn`函数将核函数应用于分类或回归任务。`fitcknn`函数的语法如下：

mo