LSTM 模型中的正向和反向传播算法原理

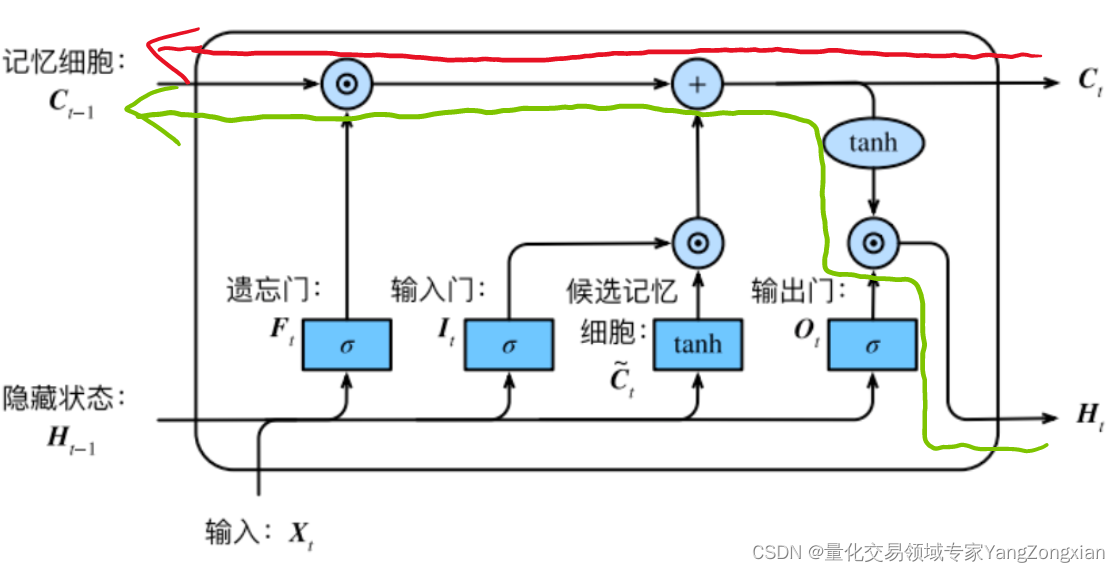
# 1. LSTM模型简介**

LSTM（长短期记忆）模型是一种强大的神经网络，专门用于处理序列数据。它通过引入记忆单元来解决传统RNN模型中梯度消失和爆炸问题，从而能够学习长期依赖关系。LSTM模型在自然语言处理、时间序列预测等领域有着广泛的应用。

# 2. 正向传播算法原理

### 2.1 LSTM单元结构

LSTM单元是一个特殊的递归神经网络单元，它由四个主要部分组成：

- **输入门（Input Gate）：**控制输入信息进入单元的程度。
- **遗忘门（Forget Gate）：**控制单元中先前状态信息的保留程度。
- **输出门（Output Gate）：**控制单元中当前状态信息的输出程度。
- **记忆单元（Cell）：**存储单元的状态信息。

### 2.2 正向传播过程

LSTM单元的正向传播过程如下：

1. **计算输入门、遗忘门和输出门的激活值：**

# 输入数据
x = [x1, x2, ..., xt]

# 权重矩阵和偏置项
W_i, W_f, W_o, W_c = ...
b_i, b_f, b_o, b_c = ...

# 计算激活值
i_t = sigmoid(W_i * [h_{t-1}, x_t] + b_i)
f_t = sigmoid(W_f * [h_{t-1}, x_t] + b_f)
o_t = sigmoid(W_o * [h_{t-1}, x_t] + b_o)

2. **更新记忆单元：**

# 计算新的记忆单元值
c_t = f_t * c_{t-1} + i_t * tanh(W_c * [h_{t-1}, x_t] + b_c)

3. **计算输出：**

# 计算输出值
h_t = o_t * tanh(c_t)

**参数说明：**

- `x_t`：当前时间步的输入数据。
- `h_{t-1}`：前一时间步的输出值。
- `c_{t-1}`：前一时间步的记忆单元值。
- `W_i`, `W_f`, `W_o`, `W_c`：权重矩阵。
- `b_i`, `b_f`, `b_o`, `b_c`：偏置项。
- `i_t`, `f_t`, `o_t`：输入门、遗忘门和输出门的激活值。
- `c_t`：当前时间步的记忆单元值。
- `h_t`：当前时间步的输出值。

**逻辑分析：**

正向传播过程通过计算输入门、遗忘门和输出门的激活值来控制信息流。输入门决定了多少新信息进入记忆单元，遗忘门决定了多少旧信息被保留，输出门决定了多少当前状态信息被输出。记忆单元存储了单元的状态信息，而输出是单元当前状态的激活值。

# 3. 反向传播算法原理

### 3.1 反向传播算法的推导

反向传播算法是LSTM模型训练过程中的关键步骤，它用于计算模型参数的梯度，从而更新参数并优化模型性能。反向传播算法的推导过程如下：

**1. 定义损失函数**

损失函数衡量模型预测与实际标签之间的误差。对于LSTM模型，常见的损失函数是均方误差（MSE）或交叉熵损失。

**2. 计算输出层的误差**

输出层误差表示模型预测与实际标签之间的差异。对于MSE损失函数，输出层误差为：

E = (y - y_hat)^2

其中：

* E：输出层误差
* y：实际标签
* y_hat：模型预测

**3. 计算隐藏层的误差**

隐藏层误差表示隐藏层神经元对输出层误差的贡献。它可以递归地计算为：

δ_t = (W_hh^T δ_{t+1}) ⊙ f'(h_t)

其中：

* δ_t：时刻t的隐藏层误差
* δ_{t+1}：时刻t+1的隐藏层误差
* W_hh：隐藏层到隐藏层的权重矩阵
* f'(h_t)：时刻t的隐藏层激活函数的导数

**4. 计算输入门、遗忘门和输出门的误差**

输入门、遗忘门和输出门的误差表示这些门对隐藏层误差的贡献。它们可以计算为：

δ_i = (W_hi^T δ_t) ⊙ i'(x_t, h_{t-1})
δ_f = (W_hf^T δ_t) ⊙ f'(x_t