【强化学习中的PPO算法：揭秘策略梯度算法的原理与应用】

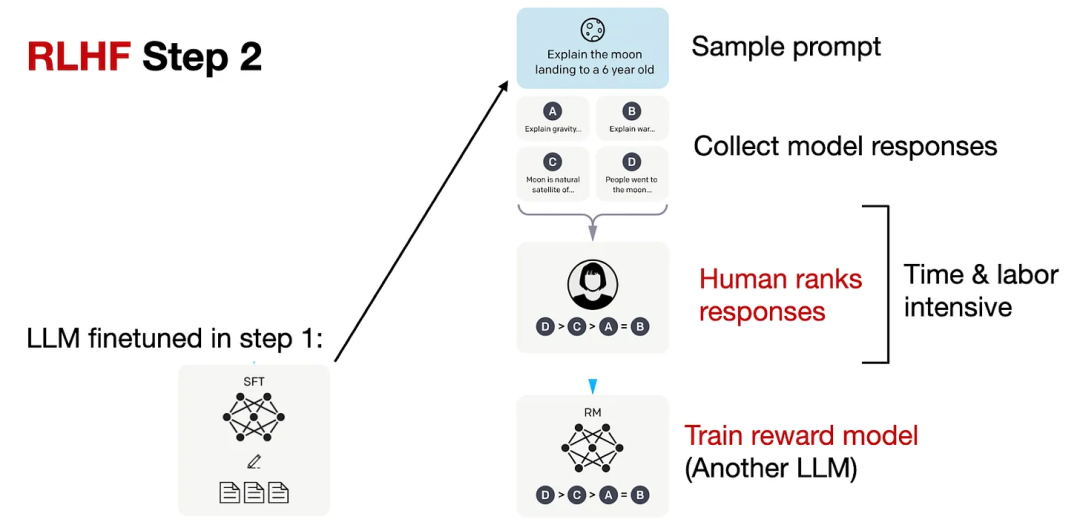
# 1. 强化学习中的策略梯度算法

策略梯度算法是强化学习中一种强大的算法，它直接优化策略函数以最大化奖励。策略梯度定理提供了策略梯度的计算方法，使得我们可以通过梯度上升的方式更新策略函数。

策略梯度算法的优点在于它可以处理连续动作空间和离散动作空间，并且不需要明确建模环境动态。它通过与环境交互并收集经验来学习最优策略，从而避免了传统强化学习方法中昂贵的动态规划过程。

# 2. PPO算法的原理与优势

### 2.1 策略梯度定理

策略梯度定理是强化学习中用于更新策略参数的数学基础。它表明，对于给定的策略π和价值函数V，策略π的梯度方向与目标函数J的梯度方向成正比，即：

∇_θ J(π) ∝ ∇_θ E[V(S_t) - V(S_0)]

其中：

* θ：策略π的参数
* J(π)：目标函数，通常为累积奖励的期望值
* V(S_t)：状态S_t的价值函数
* V(S_0)：初始状态S_0的价值函数

### 2.2 PPO算法的更新规则

PPO（Proximal Policy Optimization）算法是一种策略梯度算法，它通过限制策略更新的步长来提高稳定性。PPO算法的更新规则如下：

θ_new = θ_old + α * E[min(r_t(θ) * ∇_θ log π(a_t | s_t), clip(r_t(θ), 1 - ε, 1 + ε) * ∇_θ log π(a_t | s_t))]

其中：

* θ_new：更新后的策略参数
* θ_old：更新前的策略参数
* α：学习率
* r_t(θ)：优势函数，衡量动作a_t在状态s_t下的好坏程度
* clip(r_t(θ), 1 - ε, 1 + ε)：截断函数，限制优势函数的范围在[1 - ε, 1 + ε]内
* ε：截断阈值

### 2.3 PPO算法的优势和特点

PPO算法具有以下优势和特点：

* **稳定性高：**PPO算法通过限制策略更新的步长，提高了算法的稳定性，避免了策略更新过大导致性能下降的情况。
* **收敛速度快：**PPO算法使用了一种称为“信赖区域优化”的技术，可以加速算法的收敛速度。
* **适用于连续动作空间：**PPO算法不仅适用于离散动作空间，还适用于连续动作空间，这使其在控制任务中具有广泛的应用。
* **易于实现：**PPO算法的实现相对简单，易于与其他强化学习算法结合使用。

# 3. PPO算法的实践应用

### 3.1 PPO算法在连续控制任务中的应用

#### 3.1.1 环境搭建和模型训练

**环境搭建**

以经典的倒立摆控制任务为例，环境使用OpenAI Gym中的`gym.make("InvertedPendulum-v2")`创建。该环境模拟了一个倒立的单摆，目标是通过控制摆杆的力矩使其保持平衡。

**模型训练**

使用PyTorch实现PPO算法，模型采用一个三层神经网络，输入为环境状态（摆杆角度和角速度），输出为动作（力矩）。训练过程使用Adam优化器，学习率为0.001，训练批次大小为32。

import gym
import torch
import torch.nn as nn
import torch.optim as optim

# 环境搭建
env = gym.make("InvertedPendulum-v2")

# 模型定义
class ActorCritic(nn.Module):
    def __init__(self):
        super(ActorCritic, self).__init__()
        self.fc1 = nn.Linear(4, 128)
        self.fc2 = nn.Linear(128, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.tanh(self.fc2(x))
        return x

# 策略梯度算法
def ppo_update(actor_critic, old_actor_critic, states, actions, rewards, values):
    # 计算优势函数
    advantages = rewards - values

    # 计算策略梯度
    log_probs = actor_critic(states).log_prob(actions)
    old_log_probs = old_actor_critic(states).log_prob(actions)
    ratio = torch.exp(log_probs - old_log_probs)
    policy_loss = -torch.min(ratio * advantages, torch.clamp(ratio, 0.8, 1.2) * advantages)

    # 计算价值函数损失
    value_loss = F.mse_loss(actor_critic(states).value, values)

    # 更新模型
    optimizer.zero_grad()
    loss = policy_loss + value_loss
    loss.backward()
    optimizer.step()

# 训练过程
for episode in range(1000):
    # 采集数据
    states, actions, rewards = [], [], []
    for step in range(200):
        state = env.reset()
        done = False
        while not done:
            action = actor_critic(state).sample()
            next_state, reward, done, _ = env.step(action)
            states.append(state)
            actions.append(action)
            rewards.append(reward)
            state = next_state

    # 计算价值函数
    values = actor_critic(torch.ten