【PPO算法在离散动作空间中的秘诀：技巧与窍门大公开】

# 1. PPO算法概述

PPO（Proximal Policy Optimization）算法是一种用于强化学习的策略梯度算法。它于2017年由John Schulman等人提出，旨在解决传统策略梯度算法在不稳定性和收敛速度方面的缺点。

PPO算法的核心思想是通过限制策略更新的步长来提高算法的稳定性。它通过定义一个信任区域，在这个区域内策略更新被认为是安全的，从而避免了策略更新过大导致算法不稳定的问题。此外，PPO算法还引入了剪切函数，以进一步限制策略更新的步长，从而提高算法的鲁棒性。

# 2. PPO算法理论基础

### 2.1 强化学习基础

强化学习是一种机器学习范式，它通过与环境交互来学习最佳行为策略。它与监督学习和无监督学习不同，因为强化学习算法不会直接接收标记的数据，而是通过尝试和错误来学习。

强化学习算法通常以马尔可夫决策过程 (MDP) 为模型，其中环境的状态、动作和奖励被建模为一个马尔可夫链。算法的目标是找到一个策略，该策略最大化从初始状态到终止状态的预期累积奖励。

### 2.2 策略梯度定理

策略梯度定理是强化学习中用于更新策略的重要定理。它指出，对于一个策略 π，其目标函数 J(π) 的梯度可以表示为：

∇J(π) = ∫∇π(s, a)Q(s, a)dμ(s, a)

其中：

* π(s, a) 是状态 s 下采取动作 a 的概率
* Q(s, a) 是采取动作 a 后在状态 s 下获得的预期累积奖励
* μ(s, a) 是状态-动作分布

策略梯度定理表明，策略的梯度方向与预期累积奖励的梯度方向一致。因此，可以通过沿着梯度方向更新策略来最大化目标函数。

### 2.3 PPO算法原理

PPO (Proximal Policy Optimization) 算法是一种策略梯度算法，它通过限制策略更新的步长来提高稳定性。PPO 算法使用以下更新规则：

π(s, a) ← π(s, a) + α * min(r, 1) * ∇π(s, a)Q(s, a)

其中：

* α 是学习率
* r 是策略更新的步长限制因子，通常设置为 0.2
* min(r, 1) 是限制策略更新步长的截断函数

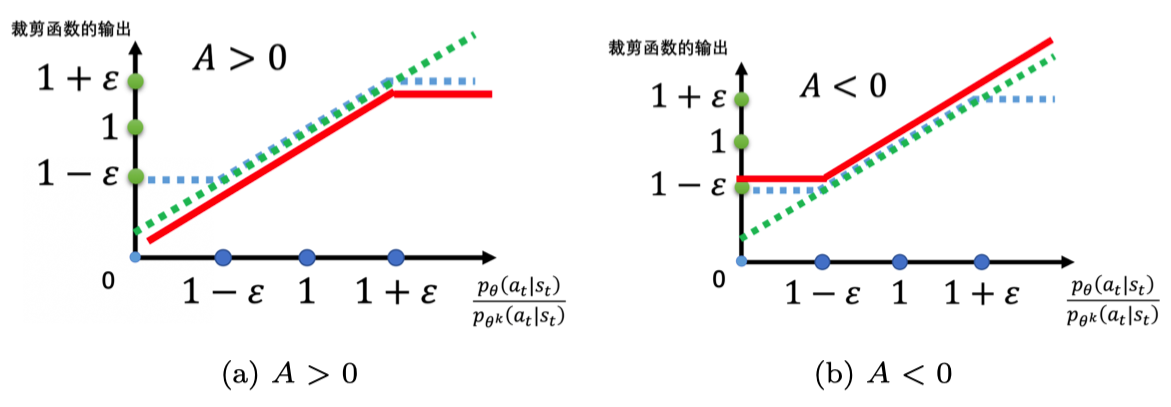
PPO 算法通过限制策略更新的步长来防止策略更新过度，从而提高算法的稳定性。此外，PPO 算法还使用了一种称为优势函数 (advantage function) 的技术来提高学习效率。优势函数衡量了采取特定动作的预期累积奖励与遵循当前策略的预期累积奖励之间的差异。

# 3.1 PPO算法的实现步骤

### 3.1.1 环境初始化

首先，需要初始化强化学习环境。环境是代理与之交互以学习和采取行动的模拟世界。对于PPO算法，环境通常是一个Gym环境，它提供了一个标准化的界面来与各种强化学习环境交互。

import gym

env = gym.make("CartPole-v1")

### 3.1.2 代理初始化

接下来，需要初始化PPO代理。PPO代理是一个神经网络，它将观察结果映射到动作。代理由一个策略网络和一个价值网络组成。策略网络输出一个概率分布，该概率分布表示在给定观察结果的情况下采取每个动作的概率。价值网络输出一个标量，表示给定观察结果的价值函数。

import torch
import torch.nn as nn
import torch.optim as optim

class Actor(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(Actor, self).__init__()
        self.fc1 = nn.Linear(state_dim, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.softmax(self.fc3(x), dim=-1)
        return x

class Critic(nn.Module):
    def __init__(self, state_dim):
        super(Critic, self).__init__()
        self.fc1 = nn.Linear(state_dim, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Li