【进阶篇】MATLAB信号处理工具箱：Signal Processing Toolbox使用指南

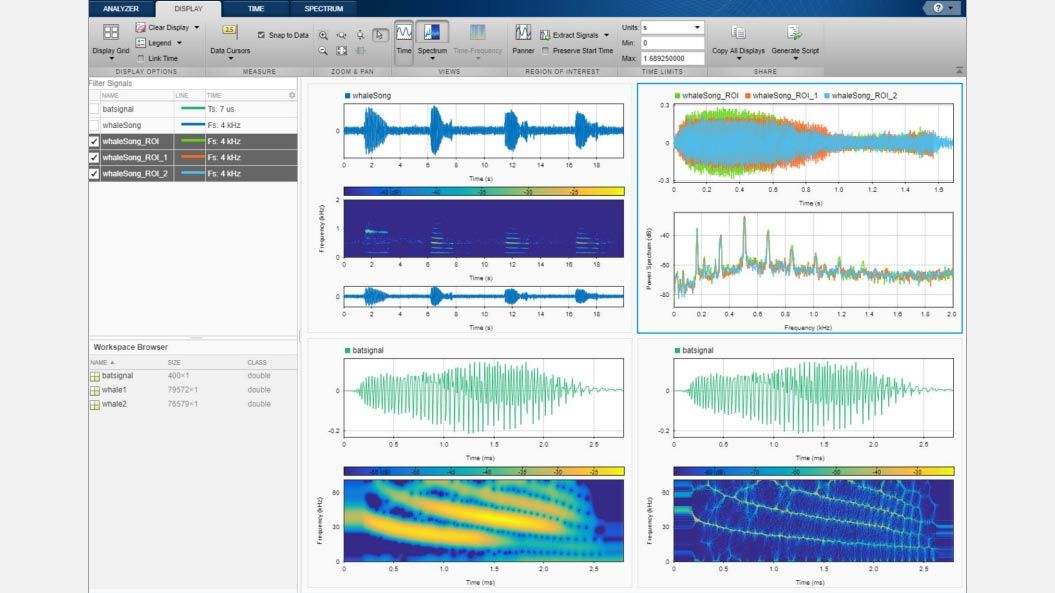
# 2.1 信号的时域和频域分析

信号的时域分析是指对信号在时间域上的变化规律进行研究，而频域分析则是对信号在频率域上的分布情况进行研究。时域和频域分析是信号处理中两个重要的基础理论，它们可以帮助我们深入理解信号的特性和规律。

在时域中，信号可以用其振幅随时间的变化来表示，而频域中，信号可以用其频率和幅度的分布来表示。时域和频域分析之间存在着傅里叶变换的关系，傅里叶变换可以将时域信号转换为频域信号，反之亦然。

时域分析和频域分析各有其优点和缺点。时域分析可以直观地反映信号的时变特性，而频域分析可以更方便地分析信号的频率成分。在实际应用中，往往需要结合时域和频域分析来对信号进行全面的理解和处理。

# 2. 信号处理基础理论

### 2.1 信号的时域和频域分析

#### 时域分析

时域分析是指在时间轴上对信号进行研究。它可以揭示信号随时间变化的规律，包括幅度、相位和频率等信息。常用的时域分析方法包括：

- **绘图：**将信号的幅度值绘制成时间序列图，直观地展示信号的变化趋势。
- **统计分析：**计算信号的均值、方差、峰值、谷值等统计量，了解信号的整体分布和波动情况。
- **相关分析：**计算信号与自身或其他信号之间的相关性，分析信号之间的相似性和相关性。

#### 频域分析

频域分析是指将信号分解成不同频率成分进行研究。它可以揭示信号中包含的频率信息，包括频率分布、谐波成分和噪声成分等。常用的频域分析方法包括：

- **傅里叶变换：**将时域信号转换为频域信号，展示信号中不同频率成分的幅度和相位。
- **功率谱密度（PSD）：**表示信号中不同频率成分的功率分布，可以识别信号中的噪声和谐波成分。
- **频谱图：**将信号的功率谱密度绘制成频率-功率图，直观地展示信号的频谱分布。

### 2.2 滤波器的设计与实现

滤波器是一种处理信号的装置，用于去除或保留信号中的特定频率成分。常用的滤波器类型包括：

- **低通滤波器：**允许低频信号通过，阻隔高频信号。
- **高通滤波器：**允许高频信号通过，阻隔低频信号。
- **带通滤波器：**允许特定频率范围内的信号通过，阻隔其他频率信号。

滤波器的设计涉及到滤波器阶数、截止频率和滤波器类型等参数。MATLAB Signal Processing Toolbox提供了丰富的滤波函数，可以方便地设计和实现各种滤波器。

### 2.3 傅里叶变换与小波变换

#### 傅里叶变换

傅里叶变换是一种将时域信号转换为频域信号的数学变换。它将信号分解成正弦波和余弦波的叠加，揭示信号中不同频率成分的幅度和相位。傅里叶变换在信号处理中广泛应用，包括频谱分析、滤波和图像处理等。

% 傅里叶变换
x = [1, 2, 3, 4, 5, 6, 7, 8];
X = fft(x);

% 绘制幅度谱
figure;
stem(abs(X));
title('幅度谱');
xlabel('频率');
ylabel('幅度');

% 绘制相位谱
figure;
stem(angle(X));
title('相位谱');
xlabel('频率');
ylabel('相位');

#### 小波变换

小波变换是一种将时域信号转换为时频域信号的数学变换。它将信号分解成一系列小波函数的叠加，揭示信号在不同时间和频率上的变化规律。小波变换在信号处理中广泛应用，包括图像处理、语音处理和生物医学信号处理等。

% 小波变换
x = [1, 2, 3, 4, 5, 6, 7, 8];
[cA, cD] = dwt(x, 'haar');

% 绘制小波分解系数
figure;
subplot(2, 1, 1);
plot(cA);
title('近似系数');
subplot(2, 1, 2);
plot(cD);
title('细节系数');

# 3.1 滤波函数

#### 3.1.1 低通滤波器

**概念：**

低通滤波器是一种允许低频信号通过而衰减高频信号的滤波器。它通常用于去除信号中的噪声或不必要的频率成分。

**MATLAB 函数：**

[b, a] = butter(n, Wn, 'low');

**参数说明：**

* **n：**滤波器的阶数，决定了滤波器的陡峭度和带宽。
* **Wn：**归一化截止频率，取值范围为 [0, 1]，表示滤波器允许通过的最高频率。
* **'low'：**指定滤波器类型为低通滤波器。

**代码逻辑：**

1. `butter` 函数使用巴特沃斯滤波器设计方法生成滤波器系数 `b` 和 `a`。
2. 巴特沃斯滤波器具有平坦的通带和陡峭的截止。
3. 滤波器阶数 `n` 越高，滤波器越陡峭，但延迟也越大。
4. 归一化截止频率 `Wn` 决定了滤波器的截止频率。

**应用：**

低通滤波器可用于：

* 去除信号中的高频噪声
* 平滑数据
* 提取信号中的低频成分

#### 3.1.2 高通滤波器

**概念：**

高通滤波器是一种允许高频信号通过而衰减低频信号的