时间序列分解：从理论基础到实际应用的完整指南

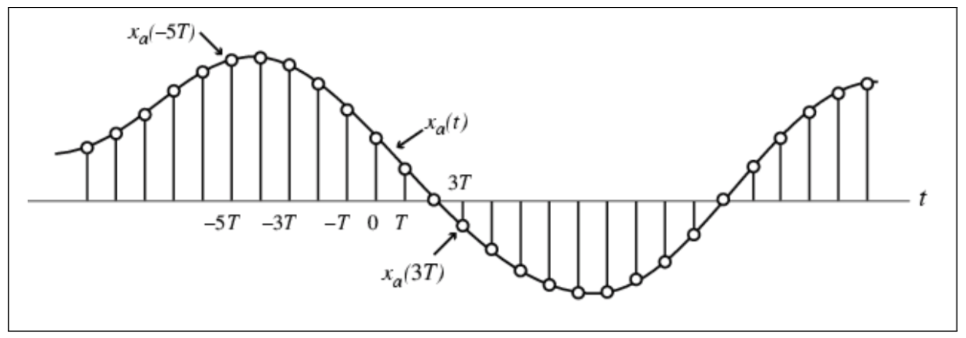
# 1. 时间序列分解的基础**

时间序列分解是将时间序列数据分解为多个组成部分的过程，这些组成部分代表了数据中的不同模式和趋势。它是一种强大的技术，可用于理解数据、进行预测和检测异常。

时间序列分解的基础在于理解时间序列的平稳性和非平稳性。平稳时间序列的统计特性随着时间的推移保持相对稳定，而非平稳时间序列的统计特性会随着时间的推移而变化。时间序列分解旨在将非平稳时间序列分解为平稳的组成部分，以便更容易分析和建模。

# 2. 时间序列分解的理论与方法

### 2.1 时间序列的平稳性与非平稳性

时间序列是指按时间顺序排列的一系列数据点。时间序列的平稳性是指其统计特性（如均值、方差、自相关）随着时间推移保持稳定。非平稳性则表示这些特性会随着时间变化。

**平稳时间序列的特征：**

- 均值恒定
- 方差恒定
- 自相关函数只与时间差有关，与绝对时间无关

**非平稳时间序列的特征：**

- 均值或方差随时间变化
- 自相关函数随时间差和绝对时间变化

### 2.2 时间序列分解的常用方法

时间序列分解将原始时间序列分解为多个分量，包括趋势、季节性、周期性和残差。

#### 2.2.1 移动平均法

移动平均法通过对原始序列进行平滑处理来去除噪声和随机波动。它通过计算指定窗口内数据的平均值来创建平滑曲线。

**代码块：**

import pandas as pd
import numpy as np

def moving_average(series, window_size):
    """
    计算指定窗口内的移动平均值。

    参数：
        series: 时间序列数据
        window_size: 移动平均窗口的大小

    返回：
        移动平均值序列
    """
    return series.rolling(window_size).mean()

**逻辑分析：**

`rolling()` 方法创建一个窗口对象，用于在指定窗口内计算统计量。`mean()` 方法计算窗口内数据的平均值。

#### 2.2.2 指数平滑法

指数平滑法通过对过去数据赋予不同的权重来平滑时间序列。它使用一个平滑系数 α，该系数决定了当前数据点对平滑值的影响程度。

**代码块：**

import statsmodels.api as sm

def exponential_smoothing(series, alpha):
    """
    计算指数平滑值。

    参数：
        series: 时间序列数据
        alpha: 平滑系数

    返回：
        指数平滑值序列
    """
    return sm.tsa.statespace.ExponentialSmoothing(series, trend='add', seasonal=None).fit(smoothing_level=alpha).forecast()

**逻辑分析：**

`ExponentialSmoothing()` 类创建了一个指数平滑模型，`trend='add'` 表示使用加法趋势模型，`seasonal=None` 表示不考虑季节性。`fit()` 方法拟合模型并返回预测值。

#### 2.2.3 ARIMA模型

自回归移动平均（ARIMA）模型是一种统计模型，用于对时间序列进行建模。它考虑了时间序列的过去值（自回归）和误差项的过去值（移动平均）。

**代码块：