【进阶】Scikit-Learn：线性回归算法详解

# 1. 线性回归算法概述**

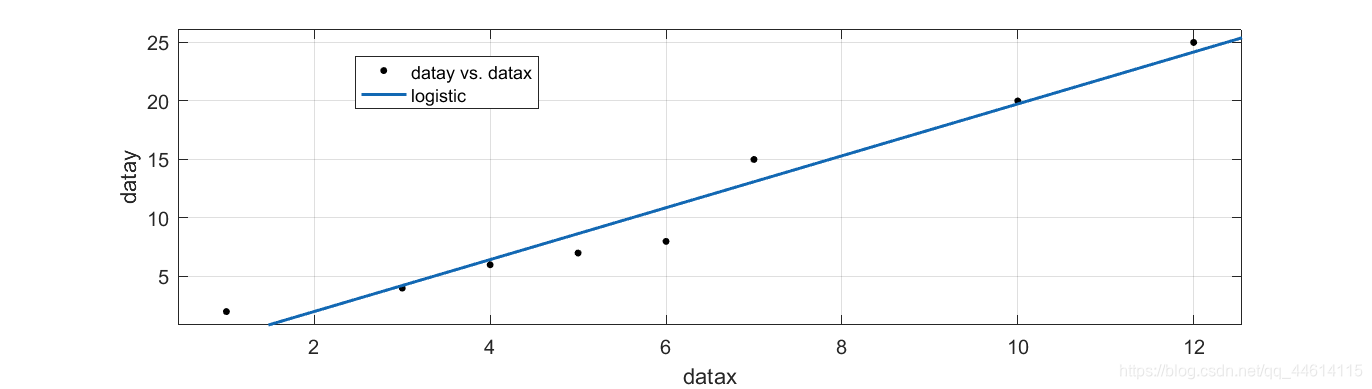
线性回归是一种监督学习算法，用于预测连续型目标变量。它假设目标变量和特征变量之间存在线性关系。线性回归算法的目标是找到一条最佳拟合直线，使预测值与真实值之间的误差最小。

线性回归算法的优点包括：

- 易于理解和实现
- 可解释性强，可以直观地解释模型中的特征和权重
- 适用于各种数据类型，包括连续型和离散型变量

# 2. 线性回归算法的理论基础

### 2.1 线性模型与最小二乘法

**线性模型**

线性模型是一种统计模型，它假设目标变量和自变量之间存在线性关系。线性模型的方程形式为：

y = β0 + β1x1 + β2x2 + ... + βnxn

其中：

* y 是目标变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是模型参数

**最小二乘法**

最小二乘法是一种用于估计线性模型参数的方法。其目标是找到一组参数，使得模型预测值与实际值之间的平方差最小。

最小二乘法公式为：

argmin(β) ∑(yi - ŷi)^2

其中：

* yi 是实际值
* ŷi 是模型预测值
* β 是模型参数

### 2.2 模型评估与正则化

**模型评估**

模型评估是评估模型性能的过程。常用的评估指标包括：

* 均方误差 (MSE)：衡量预测值与实际值之间的平均平方差。
* 均方根误差 (RMSE)：衡量预测值与实际值之间的平均平方根差。
* 决定系数 (R2)：衡量模型解释数据变异的能力。

**正则化**

正则化是一种防止模型过拟合的技术。过拟合是指模型在训练数据上表现良好，但在新数据上表现不佳。

正则化通过在损失函数中添加一个惩罚项来实现。惩罚项与模型复杂度相关。

常用的正则化方法包括：

* L1 正则化：惩罚模型参数的绝对值。
* L2 正则化：惩罚模型参数的平方值。

**代码示例：**

import numpy as np
from sklearn.linear_model import LinearRegression

# 创建数据
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) + 3

# 创建模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 评估模型
print("MSE:", mean_squared_error(y, model.predict(X)))
print("RMSE:", np.sqrt(mean_squared_error(y, model.predict(X))))
print("R2:", r2_score(y, model.predict(X)))

# 正则化模型
model = LinearRegression(alpha=0.1)
model.fit(X, y)

# 评估正则化模型
print("MSE:", mean_squared_error(y, model.predict(X)))
print("RMSE:", np.sqrt(mean_squared_error(y, model.predict(X))))
print("R2:", r2_score(y, model.predict(X)))

**逻辑分析：**

* `mean_squared_error` 函数计算均方误差。
* `r2_score` 函数计算决定系数。
* `alpha` 参数控制正则化强度。

**参数说明：**

* `mean_squared_error` 函数的参数：`y_true` 为实际值，`y_pred` 为预测值。
* `r2_score` 函数的参数：`y_true` 为实际值，`y_pred` 为预测值。
* `LinearRegression` 函数的参数：`alpha` 为正则化强度。

# 3. 线性回归算法的Scikit-Learn实现

### 3.1 模型创建与训练

#### 创建模型实例

在Scikit-Learn中，线性回归模