【进阶】深度学习基础：卷积神经网络（CNN）详解

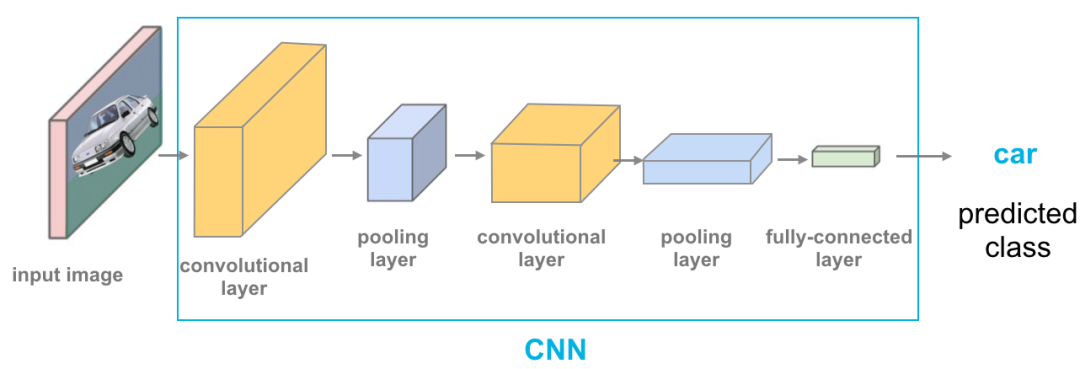
# 2.1 卷积和池化操作

### 2.1.1 卷积操作的原理

卷积操作是CNN中最重要的操作之一，它通过滑动一个称为卷积核的滤波器来提取输入特征图中的局部特征。卷积核的大小通常为3x3或5x5，它包含一组可学习的权重。

在卷积操作中，卷积核在输入特征图上滑动，并与每个局部区域的元素进行逐元素相乘。这些乘积的和被称为卷积输出，它表示该局部区域中特征的激活程度。卷积操作可以提取输入特征图中的边缘、纹理和形状等局部特征。

import numpy as np

# 定义输入特征图
input_feature_map = np.array([[1, 2, 3],
                               [4, 5, 6],
                               [7, 8, 9]])

# 定义卷积核
kernel = np.array([[0, 1, 0],
                   [1, -1, 1],
                   [0, 1, 0]])

# 执行卷积操作
output_feature_map = np.convolve(input_feature_map, kernel, mode='valid')

print(output_feature_map)

# 2. CNN的理论基础

### 2.1 卷积和池化操作

#### 2.1.1 卷积操作的原理

卷积操作是CNN的核心操作之一，它通过滑动一个称为卷积核（或过滤器）的权重矩阵来提取图像特征。卷积核的大小通常为3x3或5x5，它在图像上滑动，逐元素地与图像像素相乘，然后将结果累加起来，形成一个新的特征图。

**代码块：**

import numpy as np

# 定义卷积核
kernel = np.array([[1, 0, -1],
                   [0, 1, 0],
                   [-1, 0, 1]])

# 定义图像
image = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# 执行卷积操作
result = np.convolve(image, kernel, mode='valid')

# 打印结果
print(result)

**逻辑分析：**

* `np.convolve()`函数执行卷积操作，`mode='valid'`表示不进行边缘填充。
* 卷积核与图像逐元素相乘，然后累加，形成一个新的特征图。
* 结果是一个3x3的特征图，其中每个元素是卷积核在图像相应区域上的加权和。

#### 2.1.2 池化操作的类型和作用

池化操作是另一种重要的CNN操作，它通过将图像区域中的多个值合并为一个值来减少特征图的尺寸。池化操作有两种主要类型：最大池化和平均池化。

**最大池化：**选择区域中的最大值作为输出。

**平均池化：**计算区域中所有值的平均值作为输出。

池化操作可以减少特征图的尺寸，同时保留最重要的信息，从而提高计算效率和防止过拟合。

**代码块：**

# 最大池化
max_pool = np.max(result, axis=(1, 2))

# 平均池化
avg_pool = np.mean(result, axis=(1, 2))

**逻辑分析：**

* `np.max()`和`np.mean()`函数分别执行最大池化和平均池化。
* `axis=(1, 2)`表示沿高度和宽度维度进行池化。
* 结果是两个1x1的特征图，分别包含最大值和平均值。

### 2.2 神经网络的基本原理

#### 2.2.1 神经元模型和激活函数

神经元是神经网络的基本单位，它接收输入，经过激活函数处理后输出结果。激活函数引入非线性，使神经网络能够学习复杂的关系。常见的激活函数包括ReLU、sigmoid和tanh。

**代码块：**

import tensorflow as tf

# 定义神经元
neuron = tf.keras.layers.Dense(units=1)

# 定义激活函数
activation = tf.nn.relu

# 输出
output = activation(neuron(input))

**逻辑分析：**

* `tf.keras.layers.Dense()`创建一个神经元，`units=1`表示输出一个值。
* `tf.nn.relu`是ReLU激活函数。
* `output`是神经元的输出，它经过激活函数处理后得到非线性结果。

#### 2.2.2 反向传播算法

反向传播算法是训练神经网络的关键算法，它计算损失函数相对于网络权重的梯度。梯度用于更新权重，使网络能够最小化损失函数。

**代码块：**

# 定义损失函数
loss_fn = tf.keras.losses.MeanSquaredError()

# 定义优化器
optimizer = tf.keras.optimizers.Adam()

# 训练循环
for epoch in range(100):
    # 前向传播