【进阶】Scikit-Learn：支持向量机（SVM）

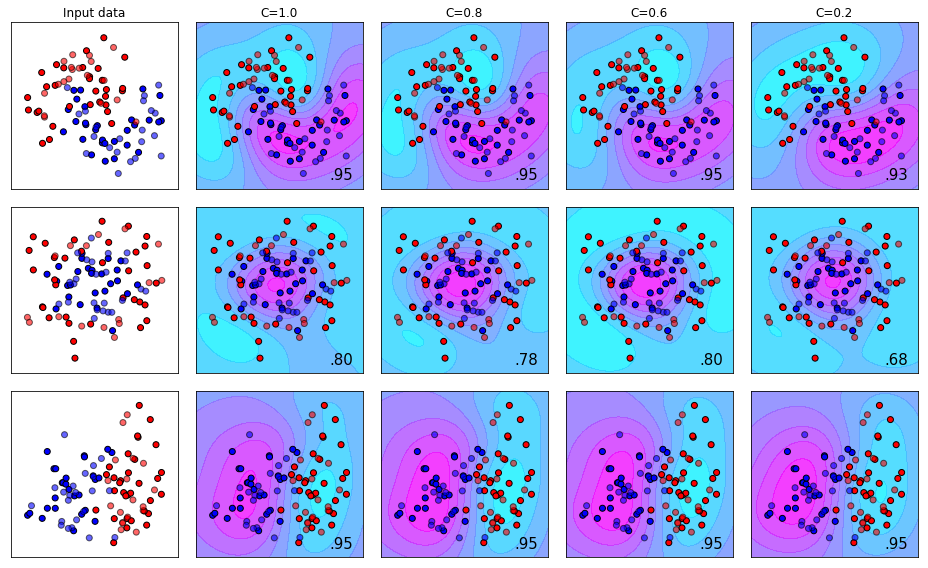
# 1. 支持向量机（SVM）概述**

支持向量机（SVM）是一种强大的机器学习算法，用于分类和回归问题。它基于统计学习理论，旨在通过寻找最佳超平面来将数据点分隔成不同的类。SVM的优点包括：

* **高精度：**SVM通常具有很高的预测精度，特别是在处理线性可分或近似线性可分的数据时。
* **鲁棒性：**SVM对噪声和异常值具有鲁棒性，因为它只关注支持向量，即影响超平面位置的数据点。
* **泛化能力：**SVM通过最大化分类间隔来优化模型，从而提高其泛化能力。

# 2. SVM理论基础**

**2.1 线性可分支持向量机**

**定义：**
线性可分支持向量机（SVM）是一种二分类算法，它通过在特征空间中找到一个超平面来将两个类别的样本分隔开。

**原理：**
* 首先，SVM算法会找到一个超平面，使得超平面与两类样本的距离最大。
* 这个超平面被称为“最大间隔超平面”。
* 最大间隔超平面两侧的样本称为“支持向量”，它们决定了超平面的位置。

**数学公式：**
给定训练数据集 {(x1, y1), ..., (xn, yn)}，其中 xi 为特征向量，yi 为类标签（+1 或 -1），线性可分 SVM 的最大间隔超平面的方程为：

w^T x + b = 0

其中：
* w 为超平面的权重向量
* b 为超平面的偏置项

**2.2 非线性支持向量机**

**局限性：**
线性可分 SVM 只能处理线性可分的样本。然而，在实际应用中，许多数据集都是非线性的。

**核函数：**
为了解决非线性可分问题，SVM 引入了核函数。核函数将输入空间映射到一个更高维的特征空间，使得样本在新的特征空间中线性可分。

**常见核函数：**
* 线性核函数：K(x, y) = x^T y
* 多项式核函数：K(x, y) = (x^T y + c)^d
* RBF 核函数：K(x, y) = exp(-γ ||x - y||^2)

**核函数的选择：**
核函数的选择取决于数据集的性质和任务。一般来说，RBF 核函数适用于大多数非线性数据集。

**参数说明：**
* c：多项式核函数中的常数项
* d：多项式核函数中的次数
* γ：RBF 核函数中的高斯核宽度参数

# 3. SVM算法实践

### 3.1 SVM模型的构建

**代码块 1：**

from sklearn.svm import SVC

# 创建一个线性核函数的支持向量机模型
clf = SVC(kernel='linear')

# 训练模型
clf.fit(X_train, y_train)

**逻辑分析：**

* `SVC()` 类用于创建支持向量机模型。
* `kernel='linear'` 指定使用线性核函数。
* `fit(X_train, y_train)` 方法使用训练数据训练模型。

**参数说明：**

* `C`：正则化参数，控制模型的复杂度。
* `kernel`：核函数类型，可以是线性、多项式、径向基函数 (RBF) 等。
* `gamma`：RBF 核函数的系数，控制核函数的宽度。

### 3.2 SVM模型的评估

**代码块 2：**

from sklearn.metrics import accuracy_score

# 预测测试数据
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)

print("准确率：", accur