【进阶】多元线性回归分析

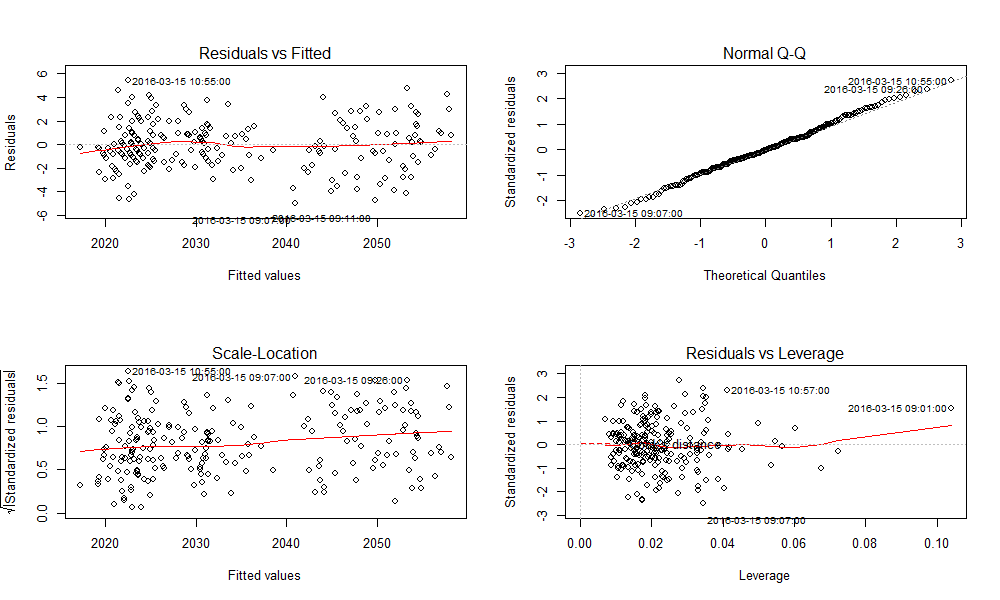
# 1. 多元线性回归分析概述**

多元线性回归分析是一种统计建模技术，用于预测一个连续型因变量（又称响应变量）与多个自变量（又称预测变量）之间的关系。它是一种广泛应用于各个领域的预测和分析工具，如经济学、金融、市场营销和医疗保健。

多元线性回归模型的数学形式为：

Y = β0 + β1X1 + β2X2 + ... + βnXn + ε

其中：

* Y 是因变量
* X1、X2、...、Xn 是自变量
* β0、β1、...、βn 是模型参数
* ε 是误差项，代表模型无法解释的因变量的变化

# 2.1 多元线性回归模型的建立

### 2.1.1 模型的假设和限制

多元线性回归模型建立在以下假设之上：

- **线性关系：**因变量和自变量之间存在线性关系。
- **正态分布：**因变量的残差服从正态分布。
- **独立性：**自变量之间相互独立，不相关。
- **方差齐性：**因变量的残差方差在所有自变量取值上保持恒定。
- **无自相关：**因变量的残差之间不存在自相关。

### 2.1.2 模型的建立过程

多元线性回归模型的建立过程如下：

1. **收集数据：**收集包含因变量和自变量数据的样本。
2. **数据预处理：**对数据进行预处理，包括处理缺失值、异常值和变量转换。
3. **变量选择：**根据相关性分析、信息准则或其他方法选择与因变量相关的重要自变量。
4. **模型拟合：**使用最小二乘法或其他方法估计模型参数。
5. **模型评估：**使用拟合优度指标（如 R²、调整后的 R²）和预测能力指标（如均方根误差、平均绝对误差）评估模型的性能。

**代码块：**

import statsmodels.api as sm
import pandas as pd

# 导入数据
data = pd.read_csv('data.csv')

# 变量选择
selected_features = ['x1', 'x2', 'x3']

# 模型拟合
model = sm.OLS(data['y'], data[selected_features])
results = model.fit()

# 模型评估
print(results.summary())

**逻辑分析：**

该代码块执行以下操作：

- 使用 Pandas 导入数据。
- 使用相关性分析选择与因变量相关的重要自变量。
- 使用 statsmodels 库拟合多元线性回归模型。
- 打印模型的摘要，其中包含拟合优度和预测能力指标。

**参数说明：**

- `data['y']`：因变量数据。
- `data[selected_features]`：自变量数据。
- `results.summary()`：模型摘要，包含拟合优度和预测能力指标。

# 3. 多元线性回归分析的实践应用

### 3.1 数据准备和预处理

#### 3.1.1 数据的收集和整理

多元线性回归分析的第一步是收集和整理数据。数据可以来自各种来源，例如调查、实验或数据库。在收集数据时，需要考虑以下几点：

- **数据质量：**数据应准确、完整且相关。
- **数据类型：**数据应符合多元线性回归模型的要求，即自变量和因变量都是数值型。
- **数据量：**数据量应足够大，以确保模型的稳定性和准确性。

#### 3.1.2 数据的缺失值处理

缺失值是数据集中常见的问题。缺失值处理方法的选择取决于缺失值的原因和模式。常见的缺失值处理方法包括：

- **