【进阶】Numpy的SVD分解

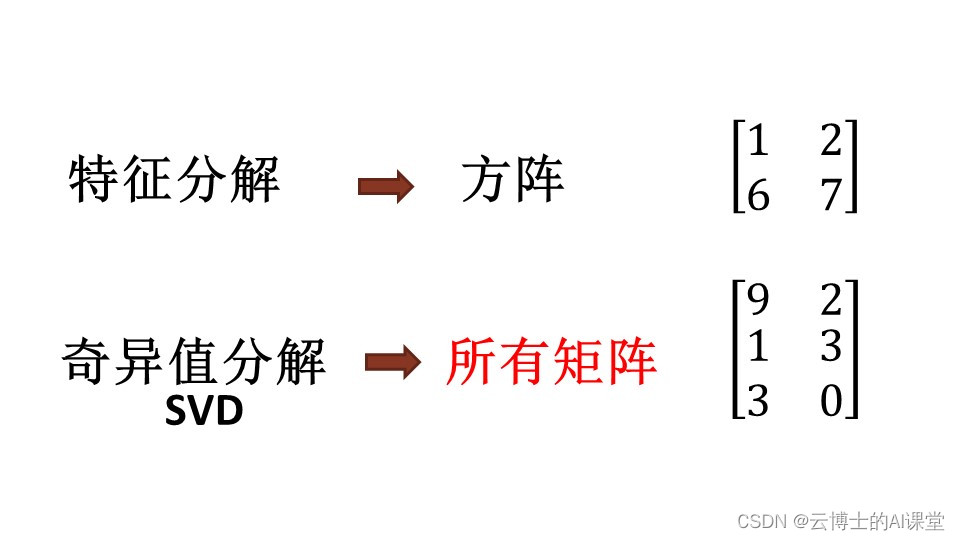
# 2.1 奇异值分解的数学定义

奇异值分解（SVD）是一种线性代数技术，它将一个实矩阵或复矩阵分解成三个矩阵的乘积：

A = UΣV^T

其中：

* **A** 是一个 **m x n** 矩阵。
* **U** 是一个 **m x m** 正交矩阵，称为左奇异向量矩阵。
* **Σ** 是一个 **m x n** 对角矩阵，称为奇异值矩阵，其对角线元素是 A 的奇异值，按降序排列。
* **V** 是一个 **n x n** 正交矩阵，称为右奇异向量矩阵。

奇异值是 A 的特征值平方根，而奇异向量是 A 的特征向量的正交基。

# 2. SVD分解的理论基础

### 2.1 奇异值分解的数学定义

奇异值分解（SVD）是一种将矩阵分解为三个矩阵乘积的数学技术。对于一个实矩阵**A**，其SVD分解形式为：

A = UΣV^T

其中：

* **U** 是一个**A**的左奇异向量矩阵，其列向量是**A**的左奇异向量。
* **Σ** 是一个对角矩阵，其对角线元素是**A**的奇异值。
* **V** 是一个**A**的右奇异向量矩阵，其列向量是**A**的右奇异向量。

**参数说明：**

* **A**：输入矩阵，可以是实矩阵或复矩阵。
* **U**：左奇异向量矩阵，是一个m×m的正交矩阵。
* **Σ**：奇异值矩阵，是一个m×n的对角矩阵，其中m和n分别是**A**的行列数。
* **V**：右奇异向量矩阵，是一个n×n的正交矩阵。

**代码示例：**

import numpy as np

A = np.array([[1, 2], [3, 4]])
U, S, Vh = np.linalg.svd(A)
print("左奇异向量矩阵：\n", U)
print("奇异值矩阵：\n", S)
print("右奇异向量矩阵：\n", Vh)

**逻辑分析：**

该代码示例使用NumPy库计算矩阵**A**的SVD分解。**linalg.svd()**函数返回三个矩阵：**U**、**S**和**Vh**，分别对应于左奇异向量矩阵、奇异值矩阵和右奇异向量矩阵的转置。

### 2.2 奇异值分解的几何解释

从几何角度来看，SVD分解可以将矩阵**A**分解为一系列正交向量（奇异向量）的线性组合。奇异值表示这些向量的长度，而奇异向量表示这些向量的方向。

具体来说，**U**的列向量是**A**的左奇异向量，它们表示**A**将空间中的向量投影到其行空间的方向。**V**的列向量是**A**的右奇异向量，它们表示**A**将空间中的向量投影到其列空间的方向。奇异值**Σ**的对角线元素表示这些投影的长度。

通过SVD分解，我们可以将矩阵**A**表示为一组正交向量的加权和，从而揭示其几何结构和线性变换特性。

# 3. SVD分解的实践应用

### 3.1 降维与数据可视化

降维是一种将高维数据映射到低维空间的技术，它可以帮助我们直观地理解和分析数据。SVD分解在降维中扮演着重要的角色，因为它可以将数据分解为一系列正交基向量，这些基向量代表了数据中最重要的方向。

#### 3.1.1 PCA降维

主成分分析（PCA）是一种经典的降维算法，它通过寻