【基础】什么是强化学习？

# 1. 强化学习的概念与原理**

强化学习是一种机器学习范式，它允许代理通过与环境交互并接收反馈来学习最优行为。与监督学习不同，强化学习不需要标记数据，而是通过奖励和惩罚信号来指导代理的学习过程。

强化学习的基本元素包括：

* **代理：**与环境交互并采取行动的实体。
* **环境：**代理所处的世界，它提供状态和奖励。
* **状态：**代理对环境的当前理解。
* **动作：**代理可以采取的可能行动。
* **奖励：**代理采取行动后收到的反馈，表示行为的好坏。

# 2. 强化学习算法

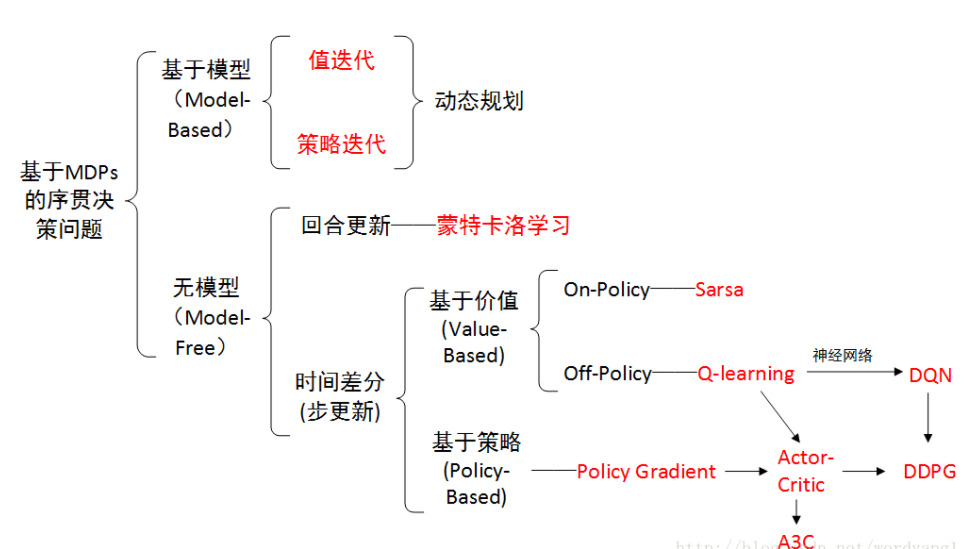
强化学习算法是强化学习的核心，它们指导智能体如何从环境中学习并做出决策。强化学习算法主要分为三类：值函数方法、策略梯度方法和无模型方法。

### 2.1 值函数方法

值函数方法通过估计状态或动作的价值来指导智能体决策。

#### 2.1.1 蒙特卡罗方法

蒙特卡罗方法是一种无模型方法，它通过模拟环境并计算每个状态或动作的长期回报来估计值函数。蒙特卡罗方法的优点是它可以提供无偏估计，但缺点是它需要大量的样本才能收敛。

**代码块：**

def monte_carlo_estimate(env, policy, num_episodes):
    """
    蒙特卡罗方法估计值函数

    参数：
        env: 环境
        policy: 策略
        num_episodes: 模拟的回合数
    """

    # 初始化值函数
    value_function = {}

    # 模拟回合
    for episode in range(num_episodes):
        # 初始化状态
        state = env.reset()

        # 轨迹
        trajectory = []

        # 循环直到回合结束
        while True:
            # 根据策略选择动作
            action = policy(state)

            # 执行动作并获取奖励和下一个状态
            next_state, reward, done, _ = env.step(action)

            # 保存轨迹
            trajectory.append((state, action, reward))

            # 更新状态
            state = next_state

            # 如果回合结束，则计算回报
            if done:
                return_ = sum(reward for _, _, reward in trajectory)

                # 更新值函数
                for state, _, reward in trajectory:
                    if state not in value_function:
                        value_function[state] = 0
                    value_function[state] += (return_ - value_function[state]) / (episode + 1)

                break

    return value_function

**逻辑分析：**

* 该代码实现了蒙特卡罗方法估计值函数。
* 它通过模拟环境并计算每个状态或动作的长期回报来估计值函数。
* 首先初始化值函数，然后模拟回合，收集轨迹。
* 对于每个轨迹，计算回报并更新值函数。
* 重复此过程，直到值函数收敛。

#### 2.1.2 时序差分学习

时序差分学习是一种在线方法，它通过逐步更新值函数来估计值函数。时序差分学习的优点是它比蒙特卡罗方法更有效，但缺点是它可能不稳定。

**代码块：**

def td_update(state, action, reward, next_state, alpha, gamma):
    """
    时序差分学习更新值函数

    参数：
        state: 当前状态
        action: 当前动作
        reward: 当前奖励
        next_state: 下一个状态
        alpha: 学习率
        gamma: 折扣因子
    """

    # 获取当前值函数估计
    value_function = get_value_function()

    # 计算目标值
    target = reward + gamma * value_function[next_state]

    # 更新值函数
    value_function[state] += alpha * (target - value_function[state])

    # 保存更新后的值函数
    set_value_function(value_function)

**逻辑分析：**

* 该代码实现了时序差分学习更新值函数。
* 它通过计算目标值和当前值函数估计之间的差值来更新值函数。
* 目标值是当前奖励加上下一个状态的折现值函数估计。
* 更新值函数时，使用学习率来控制更新的幅度。
* 重复此过程，直到值函数收敛。

### 2.2 策略梯度方法

策略梯度方法通过直接优化策略来指导智能体决策。

#### 2.2.1 策略梯度定理

策略梯度定理提供了计算策略梯度的公式，它可以用来优化策略。

**公式：**

∇_{\theta}J(\pi_{\theta}) = E_{\pi_{\theta}}[Q^{\pi_{\theta}}(s, a) \nabla_{\theta}\log\pi_{\theta}(a|s)]

**参数说明：**

* J(\pi_{\theta}): 策略 \(\pi_{\theta}\) 的期望回报
* \(\theta\): 策略 \(\pi_{\theta}\) 的参数
* Q^{\pi_{\theta}}(s, a): 状态 s 和动作 a 的动作值函数
* \(\pi_{\theta}(a|s)\): 在状态 s 下执行动作 a 的概率

**逻辑分析：**

* 策略梯度定理提供了计算策略梯度的公式。
* 策略梯度是策略参数 \(\theta\) 的期望梯度，加权以动作值函数 Q^{\pi_{\theta}}(s, a)。
* 策略梯度可以用来优化策略，通过梯度上升或梯度下降算法。

#### 2.2.2 演员-评论家方法

演员-评论家方法是一种策略梯度方法，它使用两个神经网络：演员网络和评论家网络。

* **演员网络：**输出策略，即在给定状态下执行每个动作的概率分布。
* **评论家网络：**输出动作值函数，即执行给定动作的长期回报。

**流程图：**

graph LR
subgraph 演员网络
    A[动作] --> P[概率分布]
end
subgraph 评论家网络
    S[状态] --> V[动作值函数]
end
subgraph 环境
    S[状态] --> R[奖励] --> S'[下一个状态]
end
A --> S
R --> C
S' --> C

**逻辑分析：**

* 演员-评论家方法将策略优化问题分解为两个子问题：策略优化和动作值函数估计。
* 演员网络通过最大化评论家网络输出的动作值函数来优化策略。
* 评论家网络通过最小化其输出与真实动作值函数之间的均方误差来学习动作值函数。
* 这种方法可以稳定且有效地优化策略。

### 2.3 无模型方法

无模型方法不需要环境模型，它们直接从经验中学习。

#### 2.3.1 Q学习

Q学习是一种无模型方法，它通过估计动作值函数来指导智能体决策。

**代码块：**

def q_learning_update(state, action, reward, next_state, alpha, gamma):
    """
    Q学习更新动作值函数

    参数：
        state: 当前状态
        action: 当前动作
        reward: 当前奖励
        next_state: 下一个状态
        alpha: 学习率
        gamma: 折扣因子
    """

    # 获取当前动作值函数估计
    q_function = get_q_function()

    # 计算目标值
    target = reward + gamma * max(q_function[next_state].values())

    # 更新动作值函数
    q_function[state][action] += alpha * (target - q_function[state][action])

    # 保存更新后的动作值函数
    set_q_function(q_function)

**逻辑分析：**

* 该代码实现了 Q学习更新动作值函数。
* 它通过计算目标值和当前动作值函数估计之间的差值来更新动作值函数。
* 目标值是当前奖励加上下一个状态的最大动作值函数估计。
* 更新动作值函数时，使用学习率来控制更新的幅度。
* 重复此过程，直到动作值函数收敛。

#### 2.3.2 深度Q网络

深度Q网络 (DQN) 是一种深度强化学习算法，它使用深度神经网络来估计动作值函数。

**表格：**

| 参数 | 描述 |
|---|---|
| 神经网络 | 估计动作值函数 |
| 经验回放 | 存储经验 |
| 目标网络 | 冻结的参数，用于稳定训练 |

**逻辑分析：**

* DQN 使用深度神经网络来估计动作值函数，这允许它处理高维输入。
* DQN 使用经验回放来稳定训练，它存储经验并从其中随机采样进行训练。
* DQN 使用目标网络来稳定训练，它冻结的参数，用于计算训练时使用的目标值。

# 3. 强化学习在实践中的应用

强化学习已在广泛的实际领域中得到应用，从游戏到机器人再到金融。

### 3.1 游戏领域

强化学习在游戏领域取得了显著成功，尤其是在策略游戏中。

#### 3.1.1 AlphaGo

AlphaGo 是 DeepMind 开发的计算机围棋程序，于 2016 年击败了世界冠军李世石。AlphaGo 使用深度强化学习算法，通过自对弈不断学习和改进。

#### 3.1.2 Dota 2

OpenAI 开发的 OpenAI Five 是一个强化学习驱动的 Dota 2 机器人，于 2019 年击败了人类职业玩家。OpenAI Five 使用了分布式强化学习技术，并在数百万个模拟游戏中进行训练。

### 3.2 机器人领域

强化学习在机器人领域也有广泛的应用，包括导航、规划、控制和操作。

#### 3.2.1 导航和规划

强化学习可用于训练机器人自主导航复杂环境。例如，DeepMind 开发的 MuZero 算法，可用于训练机器人玩多种棋盘游戏和视频游戏，包括国际象棋、围棋和星际争霸 II。

#### 3.2.2 控制和操作

强化学习可用于训练机器人控制和操作物理系统。例如，加州大学伯克利分校开发的 BEAR 机器人，可使用强化学习算法学习抓取和操作物体。

### 3.3 金融领域

强化学习在金融领域也得到了应用，用于优化交易策略和管理风险。

#### 3.3.1 交易策略优化

强化学习可用于训练算法自动优化交易策略。例如，高盛开发的 Gemini 算法，可使用强化学习技术学习市场动态并优化交易决策。

#### 3.3.2 风险管理

强化学习可用于训练算法识别和管理金融风险。例如，摩根大通开发的 RiskShield 算法，可使用强化学习技术学习市场风险并制定风险管理策略。

# 4.1 探索与利用的平衡

强化学习算法面临的一个关键挑战是探索与利用之间的平衡。探索涉及尝试新操作以收集有关环境的更多信息，而利用涉及利用已知信息来选择最佳操作。

### 4.1.1 ε-贪婪算法

ε-贪婪算法是一种常见的探索-利用策略。它以概率 ε 选择随机操作，以概率 1 - ε 选择根据当前策略估计的最佳操作。ε 值控制探索和利用之间的权衡。较高的 ε 值导致更多的探索，而较低的 ε 值导致更多的利用。

import numpy as np

def epsilon_greedy(Q, state, epsilon):
  """
  ε-贪婪算法

  参数：
    Q: 动作值函数
    state: 当前状态
    epsilon: 探索概率

  返回：
    选择的动作
  """

  if np.random.rand() < epsilon:
    # 探索：随机选择一个动作
    return np.random.choice(Q.keys())
  else:
    # 利用：选择动作值最大的动作
    return max(Q, key=lambda a: Q[a][state])

### 4.1.2 玻尔兹曼探索

玻尔兹曼探索是一种基于温度参数的探索-利用策略。温度参数控制探索的程度。较高的温度导致更多的探索，而较低的温度导致更多的利用。

import numpy as np

def boltzmann_exploration(Q, state, temperature):
  """
  玻尔兹曼探索

  参数：
    Q: 动作值函数
    state: 当前状态
    temperature: 探索温度

  返回：
    选择的动作
  """

  # 计算动作概率
  probs = np.exp(Q[state] / temperature) / np.sum(np.exp(Q[state] / temperature))

  # 随机选择一个动作
  return np.random.choice(Q.keys(), p=probs)

# 5. 强化学习的最新进展

### 5.1 深度强化学习

#### 5.1.1 深度神经网络在强化学习中的应用

深度神经网络（DNN）在强化学习中发挥着至关重要的作用，使算法能够从高维和复杂的环境中学习。DNN具有强大的表示能力，可以从原始数据中提取特征并学习复杂的关系。

在强化学习中，DNN通常用于：

- **状态表示：**将环境状态表示为高维向量，以便算法可以学习状态之间的关系。
- **动作选择：**根据状态表示预测最佳动作，从而指导代理的决策。
- **价值估计：**估计状态或动作的价值，为代理提供决策依据。

#### 5.1.2 强化学习在深度学习中的应用

强化学习也为深度学习提供了新的训练范例。通过将强化学习与深度学习相结合，可以：

- **无监督学习：**从环境中收集数据并通过强化学习训练模型，而无需人工标注。
- **端到端学习：**将环境感知和决策制定整合到一个统一的框架中，无需中间表示。
- **适应性学习：**使模型能够根据环境的变化自动调整其行为，提高鲁棒性和灵活性。

### 5.2 元强化学习

#### 5.2.1 元学习的概念

元学习是一种学习如何学习的方法。它使算法能够从有限的数据中快速适应新任务，从而提高样本效率。在元强化学习中，算法学习如何学习最优策略，而不是学习特定策略。

#### 5.2.2 元强化学习算法

元强化学习算法包括：

- **模型无关元强化学习：**算法学习如何快速适应新的任务，而无需对任务的具体细节进行建模。
- **模型内元强化学习：**算法学习如何构建任务的内部模型，然后使用该模型来生成最优策略。
- **多任务元强化学习：**算法学习如何同时处理多个任务，从而提高泛化能力。

# 6. 强化学习的未来展望

### 6.1 强化学习在人工智能中的作用

强化学习在人工智能领域具有广阔的应用前景，有望在以下方面发挥关键作用：

- **通用人工智能 (AGI)：** 强化学习算法可以学习在各种环境中执行复杂任务，这对于开发能够像人类一样思考和行动的 AGI 系统至关重要。
- **自主系统：** 强化学习可以使自主系统能够在动态和不确定的环境中做出决策，从而实现自主导航、规划和控制。

### 6.2 强化学习的社会影响

强化学习技术的进步也带来了潜在的社会影响，需要谨慎考虑和应对：

- **道德和伦理问题：** 强化学习算法的决策可能会受到训练数据的偏差或奖励函数的影响，从而引发道德和伦理方面的担忧。
- **经济和就业影响：** 强化学习自动化系统可能会对某些行业和工作产生影响，需要考虑其对社会经济的影响并制定适当的应对措施。