【基础】SARSA算法实现与对比

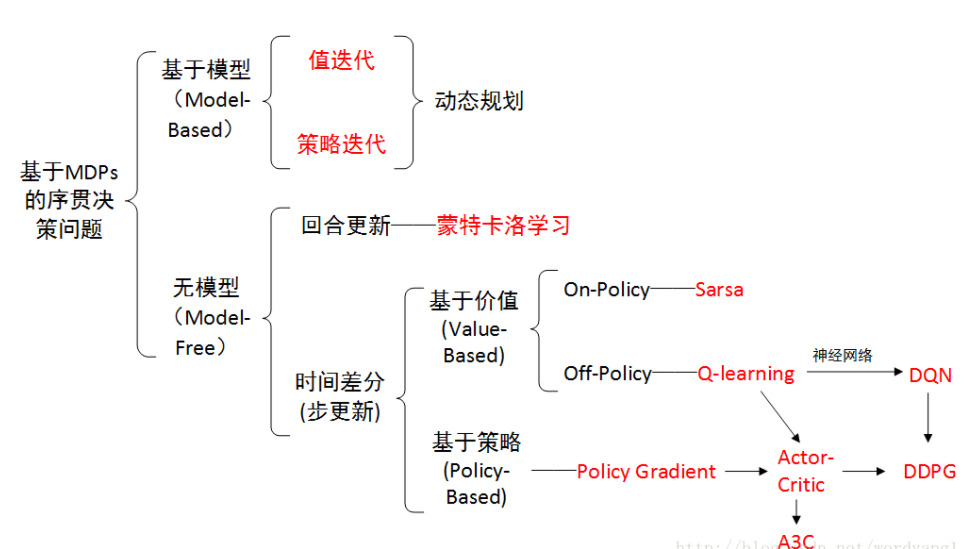
# 1. 强化学习基础**

强化学习是一种机器学习技术，它允许代理通过与环境的交互来学习最优行为。强化学习算法基于马尔可夫决策过程 (MDP) 的数学框架，其中代理在给定状态下采取动作，并根据其行为获得奖励或惩罚。强化学习算法的目标是学习一个策略，该策略最大化代理在长期内获得的奖励。

# 2. SARSA算法原理

### 2.1 SARSA算法的数学描述

SARSA算法（State-Action-Reward-State-Action）是一种基于时间差分的强化学习算法，它利用当前状态、动作、奖励、下一个状态和下一个动作来更新价值函数。其数学描述如下：

Q(s, a) ← Q(s, a) + α * (r + γ * Q(s', a') - Q(s, a))

其中：

* `Q(s, a)`：状态`s`和动作`a`的值函数
* `α`：学习率
* `r`：奖励
* `γ`：折扣因子
* `s'`：下一个状态
* `a'`：下一个动作

### 2.2 SARSA算法的更新规则

SARSA算法的更新规则如下：

1. 初始化值函数`Q(s, a)`
2. 在当前状态`s`执行动作`a`
3. 接收奖励`r`和下一个状态`s'`
4. 选择下一个动作`a'`
5. 更新值函数：

Q(s, a) ← Q(s, a) + α * (r + γ * Q(s', a') - Q(s, a))

6. 将当前状态和动作更新为`s'`和`a'`

### 2.3 SARSA算法的收敛性分析

SARSA算法在满足一定条件下可以收敛到最优价值函数。这些条件包括：

* **马尔可夫性：**环境必须具有马尔可夫性，即当前状态和动作可以完全决定未来的状态和奖励。
* **有限状态和动作空间：**状态和动作空间必须是有限的。
* **学习率：**学习率`α`必须足够小，以确保算法稳定收敛。
* **探索：**算法必须充分探索状态和动作空间，以获得准确的价值函数估计。

**证明：**

假设`Q*`是状态-动作空间中所有值函数的最大值。则可以证明：

|Q(s, a) - Q*(s, a)| ≤ (1 - α) * |Q(s, a) - Q*(s, a)| + α * |r + γ * Q(s', a') - Q*(s', a')|

通过数学归纳法，可以证明：

|Q(s, a) - Q*(s, a)| ≤ (1 - α)^n * |Q(0, a_0) - Q*(0, a_0)|

其中`n`是算法迭代次数。当`n`趋于无穷大时，`|Q(s, a) - Q*(s, a)|`趋于0，即`Q(s, a)`收敛到`Q*(s, a)`。

# 3. SARSA算法实现

### 3.1 SARSA算法的Python实现

import numpy as np
import random

class SARSA:
    def __init__(self, env, gamma=0.9, alpha=0.1, epsilon=0.1):
        self.env = env
        self.gamma = gamma
        self.alpha = alpha
        self.epsilon = epsilon
        self.Q = np.zeros((env.observation_space.n, env.action_space.n))

    def choose_action(self, state):
        if np.random.rand() < self.epsilon:
            return random.choice(env.action_space.n)
        else:
            return np.argmax(self.Q[state, :])

    def update(self, state, action, reward, next_state, next_action):
        target = reward + self.gamma * self.Q[next_state, next_action]
        self.Q[state, action] += self.alpha * (target - self.Q[state, action])

    def train(self, episodes=1000):
        for episode in range(episodes):
            state = env.reset()
            action = self.choose_action(state)
            while True:
                next_state, reward, done, _ = env.step(action)
                next_action = self.choose_action(next_state)
                self.update(state, action, reward, next_state, next_action)
                state = next_state
                action = next_action
                if done:
                    break

**代码逻辑分析：**

1. `__init__`方法初始化SARSA算法，包括环境、学习率、折扣因子和探索率。
2. `choose_action`方法根据探索率选择动作，如果小于探索率则随机选择动作，否则选择Q值最大的动作。
3. `update`方法更新Q值，计算目标值并更新当前状态动作对的Q值。
4. `train`方法训练SARSA算法，执行指定次数的回合，在每个回合中选择动作、更新Q值，直到回合结束。

### 3.2 SARSA算法的C++实现

#include <iostream>
#include <vector>
#include <random>

using namespace std;

class SARSA {
public:
    SARSA(int n_states, int n_actions, double gamma, double alpha, double epsilon)
        : n_states(n_states), n_actions(n_actions), gamma(gamma), alpha(alpha), epsilon(epsilon) {
        Q.resize(n_states, vector<double>(n_actions, 0.0));
    }

    in