【基础】特征选择方法及其实际应用

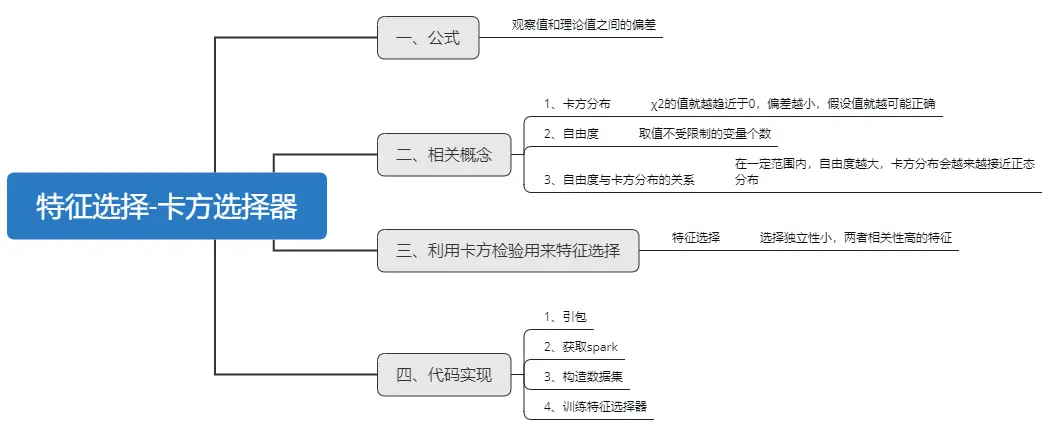
# 2.1 过滤式方法

过滤式方法是特征选择中最简单、最直接的方法。它通过计算每个特征与目标变量之间的相关性或其他统计量，来对特征进行评分。评分较高的特征被认为是更相关的，因此被保留，而评分较低的特征则被丢弃。

过滤式方法的优点是计算简单、效率高。然而，它的缺点是可能丢弃一些潜在的重要的特征，因为这些特征可能与目标变量没有直接的相关性。

# 2. 特征选择方法

特征选择是机器学习中至关重要的一步，它可以帮助我们从原始数据集中识别出对模型预测最具影响力的特征。通过去除冗余和不相关的特征，特征选择可以提高模型的性能，减少过拟合的风险，并简化模型的解释。

特征选择方法主要分为三类：过滤式方法、包裹式方法和嵌入式方法。

### 2.1 过滤式方法

过滤式方法独立于任何机器学习模型，根据特征本身的统计属性进行特征选择。这些方法的计算效率高，适用于大数据集。

#### 2.1.1 基于方差

基于方差的方法选择方差较大的特征，因为方差较大的特征通常包含更多信息。方差计算公式如下：

import numpy as np

def variance_filter(X):
    """
    基于方差进行特征选择

    参数：
    X：特征矩阵

    返回：
    selected_features：选出的特征索引
    """
    variances = np.var(X, axis=0)
    selected_features = np.argsort(variances)[::-1]
    return selected_features

#### 2.1.2 基于信息增益

基于信息增益的方法选择信息增益较大的特征。信息增益衡量了一个特征对目标变量预测能力的增加。信息增益计算公式如下：

import numpy as np

def information_gain_filter(X, y):
    """
    基于信息增益进行特征选择

    参数：
    X：特征矩阵
    y：目标变量

    返回：
    selected_features：选出的特征索引
    """
    # 计算每个特征的信息增益
    information_gains = []
    for feature in range(X.shape[1]):
        information_gain = calculate_information_gain(X[:, feature], y)
        information_gains.append(information_gain)

    # 选择信息增益最大的特征
    selected_features = np.argsort(information_gains)[::-1]
    return selected_features

#### 2.1.3 基于卡方检验

基于卡方检验的方法选择与目标变量具有显著相关性的特征。卡方检验是一种统计检验，用于检验两个变量之间是否存在关联。

import scipy.stats

def chi_square_filter(X, y):
    """
    基于卡方检验进行特征选择

    参数：
    X：特征矩阵
    y：目标变量

    返回：
    selected_features：选出的特征索引
    """
    chi_squares = []
    for feature in range(X.shape[1]):
        chi_square = scipy.stats.chi2_contingency(np.array([X[:, feature], y]))[0]
        chi_squares.append(chi_square)

    # 选择卡方值最大的特征
    selected_features = np.argsort(chi_squares)[::-1]
    return selected_features

# 3.1 数据预处理

#### 3.1.1 数据清洗

数据清洗是特征选择前必不可少的一步，其目的是去除数据中的噪声、异常值和缺失值，以提高特征选择的准确性和有效性。常见的数据清洗方法包括：

- **删除缺失值：**对于缺失值较多的特征，可以考虑直接删除，避免对后续分析造成影响。
- **填充缺失值：**对于缺失值较少的特征，可以采用插补的方式填充缺失值，如均值、中位数或众数填充。
- **处理异常值：**异常值是指明显偏离数据分布的极端值，可以采用截断或Winsorize等方法处理，将异常值替换为合理的值。
- **数据类型转换：**确保特征数据类型与后续分析要求一致，如将文本特征转换为数值特征。

#### 3.1.2 数据归一化

数据归一化是指将不同量纲的特征数据转换到同一量纲，消除量纲差异对特征选择的影响。常见的归一化方法包括：

- **最小-最大归一化：**将数据转换到[0, 1]区间内，公式为：

x_normalized = (x - min(x)) / (max(x) - min(x))

- **标准化：**将数据转换到均值为0，标准差为1的分布，公式为：

x_normalized = (x - mean(x)) / std(x)

- **小数定标：**将数据转换到小数点后固定位数，如小数点后两位，公式